|
Summer Workshops:
|
Follow-up Meetings: |
|---|---|
|
Four workshops One held in July and three in September (3½ hours each) Offering an image of high-quality inquiry teaching pedagogies |
Ten meetings Held October to May during school hours (1¼ hours each) Creating a learning community for practice-based inquiry teaching |

Teaching Mathematics through Inquiry
A Continuing Professional Development Programme Design
James Calleja
Head of Mathematics Department, Malta
&
Centre for Research in Mathematics Education, University of Nottingham, UK
Abstract
iOver the past decade, European policy makers have promoted the use of inquiry-based learning (IBL) approaches in mathematics and science. This paper describes one attempt to design an effective, replicable continuing professional development (CPD) programme that challenges the transmissive practices of teachers and that brings to awareness the pedagogical strategies required for effective IBL. This paper starts by examining IBL and then presents four features for enacting IBL in class. I will show how these four features were used as design principles for the programme – Teaching Mathematics through Inquiry (TMI) – for secondary mathematics teachers in Malta. Finally, the paper exposes the challenges faced when designing and piloting the programme. I illustrate design foundations with examples of products from the pilot project to discuss modifications and reflect on lessons learned.
1 Introduction
1Continuing professional development (CPD) is an indispensable mechanism for deepening teachers’ knowledge about content and developing teaching practices. Teaching mathematics through inquiry (TMI) is a CPD programme designed as a set of experiences where teachers have opportunities, over a one-year period, to experience, integrate, reflect upon and develop their inquiry teaching practices. This programme, designed as part of my doctoral study, is offered to secondary school teachers of mathematics as a voluntary course. In the piloting phase, held during the scholastic year 2014-2015, 5 teachers took the programme while 12 enrolled for the main study held the following year.
In this paper I present four inquiry-based learning (IBL) features and show why these are key to understanding and using IBL. Moreover, I describe how these IBL features are embedded into the programme. I draw on knowledge from large-scale projects like PRIMAS (Promoting inquiry in mathematics and science across Europe – see www.primas-project.eu) to design a programme that focuses on developing teacher knowledge and dispositions through collaborative thinking, planning and practices in IBL.
2 Inquiry-based Learning
22.1 What is IBL?
Inquiry is a multifaceted activity (Maaß & Artigue, 2013) based on student-centred, collaborative, constructivist theories and the development of higher-order reasoning. Across the literature, inquiry seems an equivocal concept – used in different ways and contexts to interpret and describe similar teaching and learning approaches such as hands-on, problem-based, project-based (Engeln, Mikelskis-Seifert & Euler, 2014), deductive and inductive approaches (see Blair, 2014). The interchangeable and loose use of the term (see Hmelo-Silver, Duncan & Chinn, 2007; Kirschner, Sweller & Clark, 2006) makes it difficult to discern and elicit clear characteristics of inquiry practice, and this raises a number of important issues. One issue that seems problematic with the term inquiry is that, while it defines an activity, it may also be seen to describe a process. In science education, for example, learning through inquiry is seen as the process of building understanding by collecting evidence and testing ideas. Like in science, mathematical inquiry starts with a problem or question but with less emphasis on practical experimenting (Rocard et al., 2007). Yet, inquiry in mathematics still involves diverse forms of activity, including: articulating or elaborating questions; modelling; exploring; conjecturing; testing, explaining, reasoning, arguing and proving; defining and structuring; connecting, representing and communicating (see PRIMAS, 2012). This understanding is in line with earlier views of Askew, Brown, Rhodes, Johnson and William (1997), Hmelo-Silver (2006) and Swan (2006), that IBL is an inductive, student-centred, collaborative approach.
IBL entails shifts in the teacher-student roles. Responsibility for learning is mostly within the students; they assume a central active role. Yet, for this to happen, the teacher must hone skills to scaffold student learning by modeling and coaching. An important aspect evident in the research literature that the TMI project values is the consideration and role that teacher guidance plays. For while discovery approaches advocate unguided instruction (Alfieri, Brooks, Aldrich & Tenenbaum, 2011), an IBL approach adheres to more thoughtful support and extensive scaffolding (see Hmelo-Silver et al., 2007) at different stages of the inquiry process. It is thus crucial to make clear this distinction to avoid running the risk of misinterpreting and confusing IBL with discovery methods – as the case of Kirschner et al. (2006) shows (see Hmelo-Silver et al., 2007).
Following on this, IBL as undertaken within this CPD programme, will refer to students’ active engagement in the learning process. Working as a community of inquirers, students become immersed in asking questions, wrestling with constructing, exploring and explaining mathematical meanings around a task set by the teacher or a question originating from the students. The task need not necessarily be open-ended but it has to provide students with an achievable challenge (see Willis, 2010), offer exploration, encourage creativity and support decision-making.
2.2 Why is IBL important for Malta in today’s world?
2In a global environment that is increasingly becoming more complex, knowledge-based, and intrinsically intertwined, with information, communications and technology the education system cannot be divested from the importance of the ability of Malta’s future adults to successfully make the transition not just into employment, but into value-laden employment.
Technological progress has shifted the demand for people capable of doing routine work to a demand for people capable of doing knowledge-based work, with a focus on the individual’s creativity and critical thinking skills so important to knowledge-based economies. In the face of such a reality, Malta’s educational system is working towards the development of learners who can manage such global effects.
Teachers are the key factor in ensuring that learners reach learning outcomes, in fostering their competences and in nurturing an inquiry stance to learning. This implies having the skills and disposition to support learners into becoming critical thinkers, responsible and active citizens. Teachers may achieve this by undertaking constructivist approaches, and research shows that IBL is an effective way to support building such competences (see Towers, 2010). Through IBL, learning opportunities are aimed at preparing young people who can create, innovate, collaborate, be critical, explore, communicate and make thoughtful decisions, hence developing key the competences and skills crucial to their lives beyond school.
2.3 How is IBL seen in the Mathematics Class?
3Mathematical inquiry requires a learner’s disposition to search for reasons and to use informed understandings for acting more responsibly in constructing knowledge. Research on the benefits of IBL gives an inconsistent picture of the effects on student learning (Maaß & Artigue, 2013). More often than not, approaches providing some form of scaffolding are found more effective in bringing about learning when compared to those offering minimal guidance (see Hmelo-Silver et al., 2007; Kirschner et al., 2006).
TMI is hence designed to support teachers in cultivating collaborative classroom environments. Through IBL teachers provide extensive scaffolding and guidance (e.g.: using purposeful questioning) to facilitate student learning. Hence, IBL is not minimally guided or unguided learning, and it is not viewed as a discovery approach.
2.4 Using a Conflict Discussion Approach for Inquiry
4Research shows that teaching can be more effective when mistakes and misconceptions are revealed and discussed (e.g. Swan, 2006). This implies that students’ ways of thinking need to be challenged by exposing them to multiple ways of solving a mathematical problem. Cognitive conflicts (see Piaget, 1985) arise when students realise inconsistencies between the methods they use and the conflicting results obtained. Research also shows that such conflicts are best resolved through discussion (Adey & Shayer, 1994; Swan, 2006). The conflict discussion approach is found to be significantly more effective for long-term learning because mistakes become visible, are tackled and resolved, rather than avoided.
Cognitive conflict is usually planned to take place over a three-phase sequence during a lesson. In the exposition phase, a teacher deliberately seeks to uncover students’ pre-existing conceptual understandings by asking students to describe or explain a particular concept or strategy. Next, a discrepant event is provided. For example, students may be asked to compare their work and responses with others or the teacher may choose to ask students to repeat a task using an alternative method. This situation creates cognitive conflict as students start identifying inconsistencies in their own interpretations and methods. Finally, in the resolution phase students engage in a reflective discussion aimed at modifying their conceptual understanding, hence resolving the misconception and ‘accommodating’ for new learning.
In an inquiry class, the conflict discussion approach may be a desirable pedagogical strategy to use. A situation that invokes conflict engages students in rethinking their thinking. When students ask questions they explicitly raise potential contradictory and inconsistent ideas. Through discussion new meanings emerge and students may have a more cognitive disposition to rectify their own conflicting situations.
2.5 The Role of the Teacher
5Orchestrating and facilitating the learning processes becomes a subtle skill that teachers need to learn and develop for IBL to function well. A common term recurrent in the literature is the role of the teacher as a facilitator in supporting student inquiry. But what does the teacher as a facilitator role entail? How can a teacher facilitate student learning through inquiry, to work collaboratively, to explore and to communicate their work? It is not only critical to define what the term facilitator implies but, more importantly, to clarify how undertaking a facilitator’s role transforms itself in the inquiry classroom. Swan (2005), for example, speaks of the teacher being a challenger and an intervener; one who asks questions to encourage and stimulate student thinking and reasoning. Such teacher assistance does not take away any agency from the students in determining the outcome of their learning. Incorporated in this is the notion of the teacher acting as an initiator, an instigator and an enabler of thinking processes throughout the lesson.
Foster (2014, p. 149) speaks of minimal interventions with the teacher ‘being fully present, interested, engaged, listening, accepting – while actively avoiding committing ideas’. The teacher does not provide answers or hints towards an answer or judgments to student responses but encourages, promotes and provokes cognitive challenges. The teacher thus offers the space for students to think, share, discuss, make decisions and come up with sound arguments and plausible solutions. Yet, the teacher also draws student attention to significant ideas emerging from their presentations providing ‘content knowledge on a just-in-time basis’ (Hmelo-Silver et al., 2007, p. 100).
Here, the interplay between the use of questioning strategies and teacher telling comes in. In an inquiry classroom, students are not left alone in their explorations. The teacher has a pivotal role in guiding students and supporting them in learning to work independently. Establishing a consensus about the nature of inquiry teaching seems a demanding task for teachers, particularly since the dilemma between exploration and telling remains unresolved (Towers, 2010). It seems to me that teachers need to strike an appropriate balance between the challenge and the learning assistance provided.
2.6 Designing and Doing IBL Lessons
6In an IBL environment, teachers respond to students in a different way than they would do in a more traditional setting. Teaching for understanding requires skills in selecting, designing and presenting inviting situations to students, managing small-group work, guiding whole-class discussions and exploiting the range of students’ solution strategies.
A typical inquiry lesson would generally incorporate the following three phases.
Phase 1: Task presentation
Teacher offers a problem, a situation, a prompt or a question stating what students are expected to do, but leaving the mathematical challenge open.
Phase 2: Small-group work
Students engage in a collaborative activity in their attempt to unravel the task.
Phase 3: A plenary
Students present their work to the whole class, providing explanations, challenging ideas and reaching agreed upon decisions.
The tasks teachers select, the way they present them to students and the way students negotiate mathematical meaning largely determine students’ classroom experiences and their learning of mathematics (Hiebert et al., 1997; Sullivan & Clarke, 1991). According to Doyle (1983, p. 161), tasks ‘influence learners by directing their attention to particular aspects of content and by specifying ways of processing information’. But, mathematical tasks are also defined by what students are required to produce and the possible routes used to obtain their solutions. Student thinking is looked into through the skillful use of questions that support students to explain their reasoning. Clearly, this may bring about some level of uncertainty for the teacher. The challenge for teachers is how to adopt this approach and how to integrate it as a basis of their teaching.
3 IBL in Professional Development
3From the vast literature of research studies on mathematics teachers’ CPD, it is clear that there has been a well-defined shift towards programmes that model effective IBL pedagogies (e.g.: Luft, 2001) with authentic activities that are similar to what teachers are expected to be doing in their classrooms (see Brown, Collins & Duguid, 1989). Jaworski (2006) is influential here arguing for two key elements: critical alignment and inquiry. CPD activities are designed to bring in ‘a critically questioning attitude towards practice and knowledge in practice that allows critical reflection on the practice of teaching’ (Jaworski, 2007, p. 1693). Teachers are not just seen to align with practice, but to look critically at that practice while aligning with it. Hence, teachers engage in inquiry as a mode of practice to develop their knowledge of practice.
3.1 Teacher Learning in Professional Development
1Theoretical understandings here assume that teachers learn just as students do, participating within collaborative support structures to build knowledge of inquiry teaching while inquiring into practices. A CPD programme would thus aim to shape the way teachers develop their identities as teachers of mathematics – by internalizing new ways of speaking, acting and thinking. Creating the space for teachers to share and question approaches to teaching is thus implicit in sustaining an inquiry stance to learning about inquiry teaching.
One important principle of CPD is for teachers to develop a meaningful interpretation of mathematical inquiry and to implement IBL effectively in their classroom. To gain this knowledge, a task-centric approach to CPD (Boston & Smith, 2011; Swan, 2007) is adopted. This implies first-hand experience working on mathematical tasks with the intent that ‘teachers can experience for themselves at their own level something of what their learners might experience and hence become more sensitive to their learners’ (Watson & Mason, 2007, p. 208). Mathematical tasks are meant to engage teachers in developing their understanding of pedagogical knowledge to inquiry teaching while, at the same time, becoming ‘more analytic and critical readers of instructional materials’ (Ferrini-Mundy, Burrill & Schmidt, 2007, p. 315).
Research into CPD gives considerable attention to the impact that community plays within teacher development and learning. In particular, CPD taking the form of a professional learning community is an appropriate way to initiate, support and sustain teacher change (Lewis, Perry & Hurd, 2009; Little, 1990). This social aspect of teacher learning highlights that teachers learn more effectively when they collaborate with others rather than when working in isolation (Levine & Marcus, 2010).
3.2 Modelling IBL through a Conflict Discussion Approach
2A key component of CPD is the role that professional learning tasks play in creating ‘opportunities for teachers to ponder pedagogical problems and their potential solutions through processes of reflection, knowledge sharing, and knowledge building’ (Silver, Clark & Ghousseini, 2007, p. 262). My own approach draws on the cognitive conflict technique and the work of Swan (2011). Similar to enacting IBL in class, the CPD approach involves a three-phase structure of activities that I will explain with reference to activities from the TMI programme.
Phase 1: The exposition phase
Teachers are invited to work on an inquiry task (see section 5.1), first individually and then in a small group. This is usually a new experience to most teachers. A whole-class discussion then follows, with prompts and questions such as:
- Comment on your experience working on this task.
- Comment on the task characteristics.
- What do you anticipate would be the challenges for students working on this task? Why? How would you address these?
- Would you consider using this task with one of your classes? Why?
- Would you present the task in a similar way as it was presented to you? Would you do it differently? Why? How?
These questions are intended to uncover teacher values, beliefs and practices, while the ensuing discussion would provide the means for teachers to share insights and experiences.
Phase 2: A discrepant event
Teachers then watch a video of a teacher using the same task in a local classroom. Alternatively, they are provided with vignettes of two teachers offering contrasting ways of using the task (see section 5.2). Teachers are again presented with a set of questions intended to challenge and help them reflect upon ways of thinking and acting in their class. For example:
- What are your comments about the lesson?
- Would you structure the lesson as the teacher did or would you do it differently?
- Who generates the mathematical ideas that get discussed? Who evaluates and/or respond to these ideas?
- How deeply do students get to explain their ideas?
- How does the teacher respond to students’ struggles?
The video and the contrasting situations usually generate a conflict between teachers’ existing practices, values and beliefs. The questions thus challenge them to reconsider pedagogical approaches and attempt to resolve their issues through discussion.
Phase 3: The resolution phase
Teachers are finally asked to plan an inquiry lesson that they would eventually use with one of their classes. Through this collaborative exercise, teachers work at resolving inconsistencies between their own pedagogical approaches and those observed.
It is important to mention that each workshop usually includes more than one cycle of the conflict discussion approach. This approach values the practice-based facet of CPD (see Smith, 2001), which is purposeful in connecting pre-existing values, beliefs and practices to new ways of promoting inquiry in the mathematics class. Within the conflict discussion approach, teachers experience tensions in their thinking. While seeking to rectify the conflict, they develop their own new meanings, hence becoming better equipped to use inquiry more effectively in their classrooms.
3.3 The Role of the CPD Facilitator
3A teacher-trainer, here referred to as CPD facilitator, needs to have the knowledge and abilities to model for teachers the appropriate processes and pedagogical actions that teachers should be doing when engaging their students with IBL. The term facilitator is used to specify undertaking the key role of empowering people in knowledge creation. A facilitator does not impart knowledge directly to the participants, but provides challenging and appealing situations for participants to wrestle with and construct their knowledge of inquiry. A facilitator needs to be skillful at probing, stimulating and supporting thinking, thus modelling IBL by immersing participants in the process of inquiry.
The role of the CPD facilitator involves guiding discussions and linking arguments to the content of the CPD. The facilitator provides scaffolds – for example, tasks, questions and prompts – to invite participants in taking an inquiry stance to learning. The CPD facilitator elicits teachers’ varying solutions to the problems and situations posed, and invites them to question one another in a supportive learning environment (Loucks-Horsley, Stiles, Mundry, Love & Hewson, 2010). Hence, the CPD facilitator needs to be sensitive in identifying key moments when more responsibility may be shifted onto the participants. When this occurs, such scaffolding is gradually removed and the community becomes its own resource for learning.
Besides developing content knowledge, the facilitator works towards building community. The role of the CPD facilitator becomes pivotal in establishing and fostering a community of learners. For a community to flourish, building trust becomes key in sustaining productive long-term learning. The facilitator needs to pay attention to the events unfolding and act without judging. It is thus important for the facilitator to create an atmosphere where teachers feel safe to share their beliefs, values and practices.
4 Features of IBL in the Mathematics Class
4From my over 20 years of experience using inquiry with students, designing tasks, and working with and observing teachers using inquiry practices, I consider IBL as a vehicle to engage students in becoming active agents within the learning process. This understanding has led me to seek key features that explain IBL and assist in the design of IBL lessons. Moreover, features of IBL may be useful in understanding not only what inquiry involves but also how inquiry may be implemented. Informed by research literature (see Askew et al., 1997; Hmelo-Silver et al., 2007; Swan, 2006) and personal understandings, I present four features that explicate IBL and inform IBL practices. The features I present are mathematical tasks, collaborative learning, purposeful questioning, and student agency and responsibility. I argue that these four features are interconnected and necessary for IBL to take place. To give an example, a teacher would shift more agency and responsibility onto students by assigning a particular mathematical task to serve that purpose, supporting students by purposefully selecting questions that prompt autonomous learning and providing an environment where collaboration supports knowledge sharing, discussion and decision making. This not to say that these features are necessarily all-inclusive, but I do contend that these provide a working framework for describing, understanding and implementing IBL.
In outlining these four features, I take a teacher’s perspective because I consider teacher’s role as crucial in selecting tasks, planning lessons, organising and managing the class, and orchestrating learning. Although the four features (see Figure 1) may appear as distinct attributes, they are not seen as stand-alone within IBL lessons. On the contrary, there is much overlap and connection between the four. This interconnected aspect is intended to emerge both during lessons with students and during the CPD workshops with teachers.
| IBL Feature | Teacher’s Role | Conditions for IBL |
|---|---|---|
| Mathematical Tasks | Teacher presents rich mathematical tasks that engage students in thinking processes while actively accessing content and making connections |
Tasks presented…
|
| Collaborative learning | Teacher provides a collaborative environment that engages students in sharing ideas, developing arguments, challenging and constructing their mathematical meanings |
The classroom culture…
|
| Purposeful Questioning | Teacher uses questions that foster reasoning and stimulate students to communicate articulated their mathematical thoughts and ideas |
Teacher questioning…
|
| Student Agency and Responsibility | Teacher provides opportunities for students to shoulder more responsibilities in learning and works to support them in becoming more active towards undertaking these roles |
Students are accountable to…
|
In the next section I present a framework with a literature rationale for drawing on these four features. This framework is intended as a guideline for using IBL in the classroom, but also for running CPD sessions with teachers. Such a framework may also be used to design a classroom observation instrument for determining teacher alignment towards enacting IBL.
4.1 Applying IBL Features to Structure CPD Content
1A major challenge for teachers seems to be adopting and integrating IBL pedagogies as part of their teaching as it requires skills alien to traditional mathematics classrooms. In enhancing this shift and to be meaningful to teachers CPD is designed around these same TMI features (see Table 2), thus sending a coherent message of IBL (Schoenfeld, 2015). For example, in conveying to teachers the significance of shifting responsibility and agency onto the students, teachers themselves need to be empowered to take meaningful control and challenge what is discussed, to try out the ideas presented, share their experiences, and adapt and construct their own theoretical perspectives of inquiry teaching. The goal of CPD is to present pedagogies that stimulate teachers to act, speak and think within an IBL perspective.
| Applying Features | IBL for Students in Schools | IBL for Teacher Development |
|---|---|---|
| Using Rich Mathematical Tasks | Introduce mathematics to students through rich tasks that provide access and opportunities to experience both mathematical content and connections | Present tasks that provide teachers with access to explore, interpret, experience and develop knowledge about mathematical inquiry (Swan, 2007) |
| Cultivating a Collaborative Culture | Integrate small-group activities for students to share ideas, develop mathematical arguments and challenge views (Swan, 2006) | Organise collaborative activities for teachers to reflect and evaluate practices, and providing new challenges and tensions |
| Fostering a Questioning Attitude | Ask questions that foster students’ reasoning, scaffold learning and stimulate them to communicate articulated mathematical ideas | Cultivate a questioning mind-set that engages teachers in deep thinking about practices, taking more active roles in developing their knowledge |
|
Shifting Agency and Responsibility in Learning |
Provide opportunities for students to assume more responsibility over their learning, arousing confidence to engage actively with mathematics (Schoenfeld, 2013) | Provide experiences that support the development of confidence in teacher capabilities to plan, implement and evaluate inquiry-based practices (Little, 1990) |
In comparing the TMI framework with the TRU Math scheme (Teaching for Robust Understanding) developed by Alan Schoenfeld (2013, 2014) which characterizes fundamentally important dimensions of powerful mathematics classrooms, I find many similarities. Schoenfeld (2015, p. 162) offers the TRU scheme and makes a strong claim that ‘a mathematics classroom that does well along these five dimensions will produce students who are powerful mathematical thinkers’. He argues that TRU applies not only to classrooms but also to learning environments, and characterizes important aspects of CPD. Table 3 below shows these five dimensions and I illustrate how my understanding of IBL in terms of the four TMI features I present, is largely aligned with the TRU Math scheme.
|
TRU Math Dimensions |
The Mathematics |
Cognitive Demand |
Equitable Access to Content |
Agency, Authority and Identity |
Uses of Assessment |
|---|---|---|---|---|---|
|
TMI Features |
Mathematical Tasks |
Collaborative Learning |
Agency and Responsibility |
Purposeful Questioning |
|
Schoenfeld (2014) argues about the importance of the mathematics so that students emerge with a rich sense of mathematics. He seems to distinguish this from the remaining four dimensions. Because while the first dimension refers specifically to ‘the mathematics’, the remaining four encompass the interactions between students and the subject – thus they may be applied to other subject areas and not necessarily mathematics. ‘Cognitive demand’ is concerned with students’ opportunities to engage productively with the mathematics. This is, in my opinion, an integral part of the mathematics offered to students and thus I see it embedded in the mathematical tasks assigned to students. I refer to tasks as those situations that offer an achievable challenge (what Schoenfeld refers to as requiring a meaningful effort) to students, thus providing a cognitive challenge. The ‘equitable access to content’ dimension pertains to the classroom activity structures that invite and support the engagement of all students. I map this to the collaborative learning feature of IBL. While I do not explicitly express the equitable aspect of mathematics classrooms as Schoenfeld does, I contend that creating a collaborative classroom climate is a powerful and effective way of engaging and including all students in the learning process. Such environments are powerful in helping students build their identities as individually accountable learners acting within a collectively responsible and supportive community of learners. The ‘agency, authority and identity’ dimension is perhaps the closest to the features I present. We both argue for students’ productive engagement in decision-making and for acting responsibly towards their learning. Finally, Schoenfeld (2014) presents the ‘uses of assessment’ dimension describing it as the extent to which student reasoning is elicited, challenged and refined. It is formative assessment since it reveals what students know and understand but also what their misconceptions are. Hence it can build on that knowledge. I link this dimension to the feature of purposeful questioning. Without claiming in any way that assessment is exclusively related to questioning, I argue that the purposeful questioning feature addresses the same dimension in a similar way – it is integral and should be an on-going component in assessing students’ learning process. Purposeful questioning refers to the extent to which questions are purposeful in fostering reasoning and in stimulating students to communicate articulated mathematical meanings.
The five dimensions presented by Schoenfeld (2014) offer a theoretical framework for mathematically powerful classrooms. Similarly, I have shown structural features for representing the teaching and learning of IBL. It seems to me that both frameworks address the question of what makes ‘good teaching’: TRU Math in terms of the end result – teaching for robust understanding, while TMI in terms of the method – teaching through inquiry. The case I make here is that, given this alignment between the two frameworks, teaching through inquiry is likely to lead to robust mathematical understanding.
4.2 The CPD Programme Structure
2Working within the Maltese context of in-service teacher training, I draw on a CPD design framework suggested by Putman and Borko (2000, p. 7). They claim that:
‘One promising model for the use of multiple contexts combines summer workshops that introduce theoretical and research-based ideas with ongoing support during the year as teachers attempt to integrate these ideas into their instructional programmes.’
This approach to the design of ‘creating opportunities to learn’ (see Goos, 2014) combines learning-off-job with learning-on-job opportunities (see Table 3). The TMI programme provides CPD experiences for teachers first through summer workshops and follow-up meetings held during the scholastic year.
The off-the-job workshops take a learner-centered approach with teachers acquiring first-hand experiences of modelled inquiry teaching. The on-the-job meetings then offer ongoing support where teachers work as a professional community to share and construct experiences of IBL (Figure 1).
5 Designing the Content of the Summer Workshops
5In designing the content for TMI, I draw mostly on two CPD initiatives promoting IBL: PRIMAS (see http://www.primas-project.eu) and Bowland Maths (see http://bowlandmaths.org). My participation in the PRIMAS project as a CPD facilitator leading a group of Maltese teachers guided my design of the materials. My immersion and first-hand experience working with teachers helped me gain knowledge about the potential of using such carefully designed CPD materials. In turn, I understood what may work better for teachers in Malta. In Table 4, I present the similarities between the modules offered by PRIMAS, Bowland Maths and the TMI programme. Modules in bold type are closely matched.
| CPD Project | PRIMAS | Bowland Maths | TMI |
|---|---|---|---|
| CPD Modules |
Tackling unstructured problems |
Tackling unstructured problems |
Mathematical tasks for inquiry |
|
Students working collaboratively |
Fostering and managing collaborative work |
Collaborative learning |
|
|
Asking questions that promote reasoning |
Questioning and reasoning |
Purposeful questioning |
|
|
Student-led inquiry |
The case studies and Mathematics |
Shifting more agency and responsibility |
|
|
Learning concepts through IBL |
Assessing key processes |
||
|
Building on what students already know |
ICT: Using resources effectively |
||
|
Self and peer assessment |
Involving students in self and peer assessment |
 Click to play
Figure 3: A Mathematical Task Involving Collaboration
Click to play
Figure 3: A Mathematical Task Involving Collaboration
 Click to enlarge
Click to enlarge
5.1 Inquiry tasks and reflective discussion questions
1PRIMAS sessions start off by providing teachers with the opportunity to reflect on their own practices either through a set of questions or by working on a task. For Maltese teachers, working on a task was seen as a better vehicle for understanding what IBL is, since they could experience it.
For example, in the ‘Human Tower’ task teachers are introduced to the ‘Human Tower’ tradition in Barcelona through a short video (Figure 2). The task (Figure 3) then invites collaboration in designing a suitable structure for building a human tower made up of three or four people (depending on the number of people in the group). This task invites creativity and the investigation of design possibilities. It promotes decision-making processes and values explorations and explanations.
 Video available at https://www.youtube.com/watch?v=xxdtZOX6AeU
Video available at https://www.youtube.com/watch?v=xxdtZOX6AeU
The next step engages teachers in a reflective discussion to link their experience working on a mathematical task with a focus on insights into how such a task may engage their students in inquiry (see Figure 4). This is one example of an activity that may create conflict discussion (see section 3.2 above).
5.2 Presenting contrasting scenarios and videos
2To facilitate the conflict discussion approach I offer contrasting scenarios. This technique of exposing teachers to opposing practices is used in two ways: (1) through teacher classroom vignettes, and (2) by presenting informal discussions between teachers. The two examples I present are taken from the purposeful questioning and the student agency and responsibility sessions.
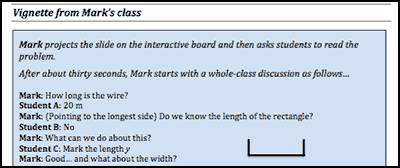
When using classroom vignettes, participants are presented with contrasting ways of how two teachers use a particular strategy in class. For example, Mark and Amy use questioning techniques to present a problem to their class (see Figure 5 and Figure 6). Participants are asked to examine the questions that Mark and Amy use. A whole group discussion is then introduced with leading discussion questions taken from the PRIMAS module guide. While both PRIMAS and Bowland Maths start off the questioning module by posing questions for teachers to reflect on their use of questioning and their purposes behind it, I prefer to offer a contrasting situation first, one that challenges teachers to think and to position themselves. I found this situation to be quite revealing in terms of stimulating teachers in genuinely saying what they do, and how they manage to identify and articulate their own gaps within the conflicting practices of others.
In the second example, two teachers, Maria and Helen, engage in a conversation discussing their roles in class (see Figure 7). Maria shoulders much of the responsibility for student learning while Helen shifts more agency and responsibility onto her students. These conflicting views are intended to provoke and elicit challenges, constraints and possibilities as perceived by participants.
 Click to play
Figure 9: Video from a local classroom
Click to play
Figure 9: Video from a local classroom
 Click to play
Click to play
My choice for using video stems from the Bowland Maths materials. In CPD programmes, incorporating videos as artifacts of practice is a valuable tool as it provides visual representations of the teaching strategies endorsed. Videos also have a distinctive ability in capturing the richness and complexity of classrooms. Brophy (2007, p. 289) argues that the best videos for analysis ‘show teachers with whom viewers can identify implementing a curriculum similar to the one they use… in a classroom similar to the classroom in which they teach’. With this understanding I created, produced and field tested videos of lessons taken in the local context supported by a selection of YouTube clips. Videos are intended to scaffold teachers’ learning and to engage in meaningful and productive discussions with others.
For example, in the collaborative learning session, teachers are shown a 3-minute video clip (Figure 8). In this clip, Dylan Wiliam discusses how teachers may set up shared group goals and individual accountability. Later, in the same session, teachers watch a lesson video from a local classroom (Figure 9) with collaborative work being the main teaching strategy adopted by the teacher.
 Video available at https://www.youtube.com/watch?v=LK_9tWsndEk
Video available at https://www.youtube.com/watch?v=LK_9tWsndEk
 Video available at https://www.youtube.com/watch?v=dT5NLZ2GQQo
Video available at https://www.youtube.com/watch?v=dT5NLZ2GQQo 5.3 Offering theoretical knowledge with lesson planning
3Another aspect common to CPD materials is exposing participants to some theoretical background knowledge and supporting them in using it. I sought to include this at two particular stages in the session design: (1) before teachers are asked to watch a lesson video, and (2) before teachers engage in lesson planning. These small doses of theoretical points (Figure 10) serve as tools for teachers to observe, interpret, analyse and plan lessons. Such an activity offers teachers the opportunity to discuss and reflect upon the issues raised, and then translate their thoughts into a lesson design.
5.4 Online CPD Materials
4 Click to visit website
www.iblmaths.com
Click to visit website
www.iblmaths.com
The ‘Teaching Mathematics through Inquiry’ website (See Figure 11 or www.iblmaths.com) was set up with a two-fold aim:to provide teachers with direct access to the CPD materials, and to support facilitators in running workshops. Besides a number of links to videos, readings and websites related to IBL, the website offers access to the slideshows, lesson videos, eight booklets for teachers and one CPD facilitator guide used during the workshops.
Both PRIMAS and Bowland Maths PD materials provide access to module guides and teacher handouts. I took up this idea to design a ‘Thinking about’ booklet for each workshop. The wording ‘Thinking about’ reflects an initial mindfulness that participants experience as they engage with the IBL features promoted.
The ‘Thinking about’ booklets assist teachers in documenting their reasoning while working on mathematical tasks, in taking personal notes and reflections, and in responding to the discussion questions presented and raised during the workshop activities. Meanwhile, a second set of booklets, referred to as ‘Planning for’, is intended as an information guide. Because it is proposed for planning IBL lessons, this serves as a resource and reference tool for teachers.
A five-page booklet is designed to provide guidelines for CPD facilitators. In this guide, the facilitator is referred to as a leader because of the key responsibility to ‘lead by example’, hence modelling IBL pedagogies during the workshop.
All four sets of the ‘Thinking about’ and the ‘Planning for’ booklets, along with the Leader's guide (Figure 12) can be browsed and downloaded at https://issuu.com/iblmaths/docs.
6 Designing Follow-up Meetings
6In what follows, I provide an outline of the four activities used in TMI sessions to conduct follow-up meetings with teachers.
Introductory Activity: Communicating Purpose
Initially, the goals of the session are communicated at the beginning. However, in time, participants actively contributed in determining goals and expectations for learning and growth.
Opening Activity: Identifying Teacher Current Knowledge
Teachers are provided with a question offering opportunities to reflect on their inquiry practices while, at the same time, providing the session facilitator with access to the knowledge that teachers bring. Teachers are typically asked about their experiences so far using IBL in their classes and about IBL aspects that are working well and those that are still challenging. Teachers write their responses on sticky notes and then either place the sticky note on the board, with the facilitator reading the responses given, or communicate their response to the whole group.
Main Activity: Exploring an Aspect of Teaching
During this part of the session participants are provided with opportunities to report back on practices, challenges and successful stories; plan lessons; and share tasks and lessons.
Concluding Activity: Eliciting Learning & Suggesting Agenda for Future Meetings
Participants describe what they learned or what they intend to do/try differently in their class next time. This is also an opportunity for them to contribute ideas on aspects that they would like to be discussed in future meetings and/or make suggestions towards potential contributions during the meetings.
7 Tools for Evaluation
77.1 Piloting the Programme and the CPD Materials
The five teachers in the pilot study chose to join this project for a number of reasons. They were either intrigued to know more about inquiry teaching, needed help to support their ‘low-achieving’ students and/or were dissatisfied with their traditional approaches to teaching mathematics.
Besides trialling the research instruments in preparation for the main study, the piloting phase served to examine the effectiveness of the CPD materials looking into possibilities for teacher learning while also testing the feasibility of the whole CPD programme. I will now focus on the data gathered and the subsequent changes implemented for the main study.
Feedback was gathered in three ways: (1) written and oral feedback received from critical friends and the CPD facilitators; (2) teachers’ written reflections and comments on the ‘Thinking about’ booklets (there was an evaluation sheet on the last page); and (3) two interviews with teachers, one following their participation in the summer workshops and one at the end of the CPD programme. Since I sought feedback on the effectiveness of the CPD materials on teacher learning and the feasibility of the CPD programme, the participants were the most important contributors. Understanding that it could be awkward for them to be critical, I emphasised that I was piloting the programme and required feedback to make the necessary improvements.
Critical friends who attended the summer workshops provided feedback as non-participatory observers. They were two education officers, a doctoral student conducting a similar study with science teachers and the two persons leading the workshops (as these were having a first-hand experience using the CPD materials). I knew my critical friends well and had established a very good professional working relationship to trust that they would provide sincere analytical comments (see Figure 13 for the questions for feedback).
Feedback Questions for CPD Facilitators
How would you describe your experience leading the session/s?
How would you rate the PD materials used in terms of effectiveness in
engaging teachers in thinking and discussing IBL?
What is your opinion of the sequence in which the four workshops were designed?
Was there enough time for teachers to carry out the tasks assigned?
Which materials worked well and which ones need to be improved? What
changes would you suggest?
To what extent do you think such a program is replicable? Do you think the materials made available on the website (PD booklets, Powerpoint presentations, video clips etc.) provide enough guidelines for someone interested in implementing this program somewhere else?
Feedback Questions for Critical Friends
How would you describe your experience observing the session/s?
Were the PD materials effective in engaging teachers in thinking and
discussing IBL? In what ways?
What is your opinion of the sequence in which the four workshops were designed?
Was there enough time for teachers to carry out the tasks assigned?
Which materials worked well and which ones need to be improved? What
changes would you suggest?
What is your opinion of the PD booklets provided to teachers during the session?
7.1.1 Summer Workshops: Insights into sessions and IBL features
2Here I outline and discuss the main findings emerging from piloting the four summer workshops.
Finding 1
The four IBL features presented during the workshops were equally important and largely interconnected. This interconnectedness emerged during each workshop discussion and during the follow-up meetings. Indeed, it was highly improbable for workshop discussions to stick to just one of the four IBL features of the CPD programme without touching upon and making links to the other three features.
Finding 2
CPD activities deal with specific aspects of inquiry teaching, and explore pedagogical challenges that arise when introducing IBL. The whole ‘package’ is conceived as a puzzle of activities that provide a network of professional learning opportunities. Thus, when leading workshops, CPD facilitators need to ensure and support discussions that deviate from the particular IBL feature being presented, providing links as necessary. Yet, one question remains: “Which session should be offered first?”
Finding 3
Some rethinking and redesigning of the ‘Mathematical Tasks’ workshop was necessary as teachers requested more opportunities to look into a wider range of tasks, to reflect, discuss and select those that supported their planning of future lessons. In particular, teachers requested tasks that directly incorporated the mathematical content they had to teach.
Finding 4
Of all the four workshops, ‘Shifting Agency and Responsibility’ was novel to teachers and emerged as key for them in understanding IBL practices. Teachers also remarked that they benefitted especially from videos of local classrooms explicating inquiry strategies, and the subsequent discussion.
Finding 5
The introductory activity of having teachers work collaboratively on a mathematical task turned out to be extremely helpful for teachers in understanding IBL. As one teacher wrote, “I thought working on tasks was going to be easy, yet it was challenging and intriguing. It was inspiring as I could experience inquiry from the students’ perspective”.
Finding 6
The conflict discussion approach was beneficial in offering tasks and scenarios for teachers that presented a mismatch between their existing beliefs, values and practices. Opportunities to identify, modify and eventually try to align these with inquiry practices supported their development and learning of using IBL.
7.1.2 Follow-up Meetings: Key outcomes
3Follow-up meetings sought to promote, build and sustain community development and learning by: (1) providing a safe, supportive and collaborative environment; (2) cultivating reflective practices; and (3) sustaining on-going engagement. In what follows, I outline key emerging insights that may be crucial to develop professional learning communities.
Initial engagement within the community
Participants were initially hesitant to share ideas and communicate their limitations. It was a bit difficult to ‘break the ice’ and get them into the discussion. For example, they found it difficult to build on what others were saying and seemed reluctant to disagree and challenge ideas presented. This, I feel, was because they did not know each other well; the community presented a new setting and possibly a new way of learning about teaching for most of them; and initially participants felt they had limited experience and expertise with IBL practices. Hence, they perceived themselves as lacking in the contributions they could make. Over time, teachers started to develop more knowledge about IBL and as a result, they sought more sustained support from within the community. This was particularly evident for the three teachers who did not have a colleague with whom to work within their particular school. These teachers looked forward to attending the meetings and regarded these as lifelines to persisting with IBL.
Taking on a reflective stance to practice and learning
Teachers regularly wrote in their lesson journal and this turned out to be an important supporting tool for reflection. The journal assisted teachers to become more active in contributing to discussions, questioning and in trying to find answers to questions related to their classroom practices. Over time, teachers were more able to transfer their learning from the community and into their classrooms. They also demonstrated increased confidence in taking a more leading role – reflecting, planning, implementing and then bringing back classroom knowledge to the community.
Providing on-going engagement
To develop active engagement and a reflective stance to practice, teachers need time. Hence, providing sustained on-going meetings is crucial. Teachers met on a regular basis ten times during one whole scholastic year with meetings lasting for 1¼ hours. A meeting of 1¼ hour might seem short for engaging participants in discussion but this was the maximum time slot possible, given that meetings were carried out within school hours and most had to plan time for travelling. I would say that a slightly longer session time would have been beneficial for activities involving collaborative lesson planning. Yet, teachers felt happy with this time frame as it kept them focused on the activities. Generally speaking teachers seemed to be saying that the quality of the discussions they engaged in was more important and longer periods would not necessarily produce more or better learning for them. Later into the scholastic year, teachers requested to meet more frequently – every two weeks rather than once every month. It seems that the teachers felt the need for increased community meetings to maintain the momentum they had gained with their inquiry practices.
7.2 Lessons Learned on Designing and Delivering CPD
4With the theoretical understandings underpinning this CPD programme, I voice reflections about what emerged following the piloting of this intervention. I also explicate lessons learned that might be useful for future CPD initiatives taking place in similar contexts and reflect on aspects related to general features of delivering CPD within the TMI programme design.
This CPD programme asked teachers to assume greater agency and become inquirers themselves in their professional development journey. I contend that this was no straightforward position for the five Maltese teachers to assume. For some this ‘new’ active role towards professional learning offered some challenge with regards to accepting and undertaking new ways of working. Hence, the first lesson speaks about the initial challenges that teachers may encounter in a professional learning community. This is likely to be evident in the initial phase of the CPD journey because of an enculturation process that teachers need to go through in acquiring new norms of being, participating and learning within a community.
During workshops CPD facilitators may seek to cover as much PD material as possible. But this may not necessarily mean that teachers would gain more. This situation appears analogous to that of the classroom – with a mathematics teacher attempting to ‘deliver’ and ‘cover’ as much content as possible at the detriment of the learning taking place. While CPD facilitators rightly try to communicate the ‘whole package’ of a CPD programme, my evidence shows that ‘covering more’ does not necessarily translate to better learning. Thus CPD facilitators need to be sensitive in gauging teachers’ engagement and be cautious to manage sessions at a pace that keeps teachers receptive, active and involved. The piloting phase also indicates that, initially, the CPD facilitator may need to lead and support teacher learning. Over time, scaffolding could be gradually removed to allow for increased teacher autonomy.
This argument brings me to a second lesson learned – making time for teachers to share ideas openly, often and formally. Besides cultivating a safe and non-judgmental environment, it is crucial to plan for adequate quality time for teachers to do this. Allowing teachers the time to share their practices in an unhurried atmosphere paves the way for practical and personal knowledge to be shared, considered, evaluated and eventually improved. Providing 1¼-hour slots with increased frequency of meetings over one whole scholastic year impacted positively towards ensuring a high-quality CPD experience for the teachers.
Participants also remarked that they would have benefitted from support at school, possibly from a colleague. One possible strategy to begin building such communities in the participating schools would be to request that pairs of teachers, rather than individuals, become involved in such a project, and then to bring all the teachers together so they could share ideas and challenges, and seek solutions amongst colleagues from their own and other schools (see Goos, Dole & Makar, 2007). Hence, a third lesson applied to the main study is that of inviting pairs of teachers from each school rather than looking for individuals.
8 Concluding Remarks
8In this paper I described how an understanding of IBL based on four features guided my design of a CPD programme, and how IBL in professional development sought to mirror IBL as promoted in class. I also illustrated and discussed how a conflict discussion approach offered a guiding framework towards conveying IBL through these four features, highlighting the challenges, insights and outcomes of designing and conducting CPD. Developing a CPD intervention programme like TMI is a challenging venture – designing and conducting the programme, and creating the space for teachers to meet. This is especially true for countries like Malta where the culture of cultivating learning communities, practice-based and ongoing components to CPD, and collaborative structures and practices are still relatively new and under researched.
Acknowledgements
iiI acknowledge the support received from Malta’s Ministry of Education, the participants and the heads of schools for providing access to visit classrooms and for making timetable arrangements for teachers to attend the follow-up meetings. I would also like to thank the Malta Government Scholarship Scheme grant for partially funding the research work disclosed in this publication. Last but not least, I would like to express my gratitude to Malcolm Swan, Hugh Burkhardt and Colin Foster for valuable comments provided on earlier drafts of this paper, as well as the editor and the two anonymous reviewers for the very helpful suggestions they offered.
References
iiiBowland Maths (2008). Bowland Maths: Imaginative resources for rich problem solving in secondary school Maths. Bowland Charitable Trust. Available from http://www.bowlandmaths.org
Engeln, K., Mikelskis-Seifert, S., & Euler, M. (2014). Inquiry-based mathematics and science education across Europe: A synopsis of various approaches and their potentials. In C. Bruguière, A. Tiberghein, & P. Clément (Eds.), Topics and Trends in Current Science Education. (pp. 229-242). Netherlands: Springer.
Jaworski, B. (2007). Theory in developmental research in mathematics teaching and learning: Social practice theory and community of inquiry as analytical tools. Proceedings of the 5th Congress of the European Society for Research in Mathematics Education. (pp. 1688-1697). Cyprus: Department of Education, University of Cyprus.
PRIMAS. (2012). Promoting Inquiry in Mathematics and Science across Europe. Project website link: http://www.primas-project.eu
About the Author
ivJames Calleja has been teaching Mathematics in secondary schools for the past 21 years. He is also a Head of Department and a part-time lecturer at the University of Malta. Over the past 6 years he has worked on a number of projects with teachers to promote inquiry-based learning and formative assessment (see www.investinmathsense.wordpress.com). James is a part-time PhD student at the Centre for Research in Mathematics Education in the School of Education at the University of Nottingham. His research interests include designing IBL mathematical tasks and continuing professional development.