Let me begin by giving credit where credit is due: the concept of professional vision is due to Charles Goodwin (1994) in a paper with that title. There is a telling photograph on page 610 of Goodwin’s manuscript. In it, an archaeologist uses a trowel to draw a circle in a patch of dirt. The encircled dirt is mottled, with some circular and some square(ish) patches of lighter or darker-colored dirt. Inside the circle, according to the archaeologist, is a square “post mold” – all that remains of a post that once supported an ancient house. There is no wood, just a patch of differently colored dirt after some centuries of decomposition. To the archaeologist’s eye, the evidence is clear. To my eye… well, Goodwin doesn’t say whether the post mold is darker or lighter than the surrounding dirt, so I’m not sure. There’s a darkish square toward the top right of the circle, and a lighter though more mottled square toward the bottom. If post molds are darker, which is what I’d guess, then it’s probably the one near the top (see Figure 1). But that’s the point. Where I can barely guess at something that is vague and – to my mind, almost impossible to differentiate – the post mold is quite clear to the anthropologist, as a result of his hard-earned professional vision. What is there to be seen is a function of knowledge as well as perception. Indeed, anthropologists literally have a tool kit for helping with such differentiations: a color chart with holes in each swatch of color so that a person can lay the chart over an object to be color-classified and make a precise match with the color of the object. (See Goodwin, in press, for an elaboration of these ideas and a discussion of the mechanisms by which professional vision operates.)

Bridging the Cultures
of Educational Research and Design
Alan H. Schoenfeld
Elizabeth and Edward Conner Professor of Education
University of California, Berkeley
Abstract
1There is some but relatively little overlap between the cultures of educational research and educational design, a state of affairs that is to the detriment of both fields. In this article I address some of the reasons this is the case, and then make a plausibility argument for a more substantial rapprochement between the two fields. I do so first by analogy, suggesting that research on the “professional vision” of designers would be of profit to practitioners in both fields. I then provide a preliminary example of what such work might reveal, and propose the systematic pursuit of such ideas.
Introduction and overview
2This article addresses four main questions:
- Can Educational Research and Educational Design live in happy synergy?
- Why haven’t they, for the most part?
- What reason is there for the two fields to collaborate?
- What mechanisms might result in increased collaboration, to the benefit of both fields?
These questions are premised on the fact that the research and development communities in education are largely separate enterprises, worldwide. In addition, there is a significant asymmetry: Educational researchers number in the tens of thousands and organizations such as the American Educational Research Association (AERA, http://www.aera.net/) and the European Association for Research on Learning and Instruction (EARLI, http://www.earli.org/) have large memberships and established traditions, whereas professional educational designers number in the hundreds and the International Society for Design and Development in Education (ISDDE, http://www.isdde.org/), the only society of its kind in education, is in its institutional infancy.
It should be noted that there are a small number of institutions where research and design coexist happily. One can point to TERC and the Lawrence Hall of Science in the U.S., the Shell Centre in England, the Freudenthal Institute in the Netherlands, and various groups in France (e.g., the community of researchers surrounding the development of CABRI geometry) as institutions at which educational research and educational design and development have commingled through the years, to mutual benefit. But these are, in the original etymological sense of the expression, “the exceptions that probe the rule.”
For now, leaning on the examples identified in the previous paragraph, I shall simply assert that the answer to the first above question is “yes;” there are clear indications that researchers and designers can and do profit from close interactions with each other. Supporting detail for greater synergy will come increasingly through this article (see also Schunn, 2008). My discussion of the second question will briefly reprise the argument in Burkhardt & Schoenfeld (2003), which identifies disincentives within each community for closer ties with the other. I then proceed with a specific rationale for forging closer connections, the idea of unpacking designers’ “professional vision.” This is done with an elucidation of the idea as it arose in the research literature, followed by a brief example grounded in the pages of this journal. I end with some suggestions about ways in which the endeavor might be moved forward.
The problem: Separate and unequal.
3There is a face value case that research and design have a lot to learn from each other.
On the one hand, a significant percentage of research studies explore the impact of investigator-designed educational interventions. Surely these would be improved if the investigators could rely on accessible and useful principles of design, and the interventions themselves were more professionally done. I can speak autobiographically here. For example, I got some quick lessons before my very first educational experiment, when a more experienced designer colleague ripped my instructional design to shreds, explaining that “if you highlight everything, then nothing stands out.” Later, an assessment task I had created was tremendously improved when a designer, using what I was to learn was one of his standard design heuristics, was able to halve the number of words in a rather long-winded task statement. And, after only a very brief look at some software my research group had developed, a well-known software designer was able to suggest a number of shortcomings of, and potential improvements to it. Clearly, knowledge of and access to design skills and heuristics could have made my own efforts more effective. Needless to say, I am hardly an isolated case when it comes to researchers who could learn a great deal from designers and/or the codification of design knowledge.
On the other hand, designers stand to learn a fair amount from researchers, who have a wide range of techniques for finding out what sense students are making (or not) of attempts to teach them or assess their knowledge. To give a personal anecdote once again, for some years I served on the committee that designed a highly consequential examination taken by graduating mathematics majors when they applied for graduate studies in mathematics. The calibration of scores was done statistically, using “equator items.” When one of the test committee members mused about how students might actually be solving the problems (e.g., a long way, a clever way, or by elimination of alternative choice options), I suggested a number of ways that student work could be sampled to provide insights into such questions. The exam committee was unfamiliar with these.
More generally, I note that in the U.S., the National Council of Teachers of Mathematics’ (1989) Curriculum and Evaluation Stands for School Mathematics, the backbone of “reform” mathematics and reform curricula, was firmly grounded in contemporary research in mathematical cognition; in that sense the desiderata for curriculum outcomes were research-based. But, the designers of Standards-based curricula consistently told us that they did not have the time to engage in detailed research on how their curricula were working[1] – the time pressures to produce curricular units on schedule were too large. Subsequent to the notable success of some of these curricula, the creators of at least two of the major Standards-based curricula have expanded their research programs. But, one can argue that formative research might have produced earlier or more robust improvements; and, as argued below, designers as a community can profit from the elucidation, via research, of design knowledge.
Differing reward structures for the two fields, Educational Research and Educational Design and Development (henceforth ER and EDD respectively), contribute to the divide between the two fields. Given that Hugh Burkhardt and I have written about this at some length (see Burkhardt & Schoenfeld, 2003), I will summarize briefly here.
The promotion and tenure system for academics such as myself tends to provide consistent disincentives for engaging in more than minimal design and development. The “best” kind of article to get published is a single-author research contribution to a major journal; if there is a design or development component to the work, it is usually considered ancillary, as something that enabled the research to be conducted, rather than of value itself.
In recent years there has some hope for attention to design through the emerging form of “design experiments” (Cobb et. al., 2003; Schoenfeld, 2006), which do pay appropriate homage to both ER and EDD, and to the potential synergy between them. The author’s experience as reviewer, however, has been that few researchers understand the need for design-theory dualism in design experiments. Properly construed, a design experiment consists of the creation of an instructional intervention on the basis of a local theory regarding the development of particular understandings. The intervention is then examined with regard to the accuracy of the underlying local theory and the power of the intervention, with an eye toward refining both. Doing so thus calls for having a solid theoretical perspective and for possessing design skills, two talents rarely found in one individual. This raises the issue of design teams as part of the research endeavor.
Generally speaking, the more authors there are on a piece, the less credit is assigned to each individual; hence the kind of teamwork necessary to produce high quality design results in less credit per capita. (Having one’s name listed as part of the “et al.” is the academic equivalent of being banished to citation Siberia.) The quickest way to rise as an academic is to have a body of work that is attributable to oneself in name – “When you think of Professor X, this body of work comes to mind, and conversely, when someone names this body of work, you think of Professor X.” (Of course, when there is a design effort of any magnitude, the work is typically done by a team. Interestingly, those scholars whose work has involved a large amount of design tend to have collaborated as members of design teams, but to have written research papers with at most one or two co-authors, if any.)
Similarly, researchers face disincentives for the kind of perseverance that results in the effective refinement of instructional materials over time. New ideas or new materials get new credit, but if one pursues the same track for too long, one might be seen as being in a rut. To give a specific example: for many years the funding policy of the U. S. National Science Foundation has been to emphasize innovation. Thus, new and interesting ideas – for example, new technological environments for learning – were encouraged. But, requests for second or third rounds of funding, which would have stabilized and improved those learning environments, were often denied on the grounds that the proposed work was no longer innovative. This, in effect, cancelled development before the work was ready for large-scale use. (And, of course, seeking such large-scale use outside the officially sanctioned R&D channels may be seen as a sign that one is not serious about one’s research career.) Finally, building on someone else’s ideas or refining someone else’s materials can be seen as somewhat derivative, and thus dangerous to one’s career.
In sum, at many research universities those inclined to conduct EDD do so at some risk. The exceptions (e.g., the homes of some of the NSF-funded curriculum projects, which did manage to have respectable half-lives) probe the rule, but by and large, individuals with primary interests in design find it hard to thrive in academia. Indeed, the histories of some of the world’s most notable academic design groups include periods of high risk, where international campaigns were waged to convince the home institutions that the groups were well-enough regarded to keep alive.
Some of the constraints on the design side were mentioned above. The primary goal of design is to produce materials that make a difference[2]; anything that diminishes attention to that primary goal is potentially problematic, and will tend to be minimized. EDD is typically an entrepreneurial activity carried out by commercial developers, design houses (in the U.S. institutions such as TERC or the Lawrence Hall of Science), or design groups housed within universities. For commercial companies, the main concerns and incentives are fiscal. For example, when I served on California’s mathematics standards committee soon after the NCTM Standards were published, representatives of commercial publishers told us that they simply would not undertake development costs for materials like those envisioned in the Standards: it cost $25 million to produce a text series for grades K-6, and that the even larger investment needed to design and develop an innovative, and essentially untested, product was unthinkable. (This expression of commercial realism confirmed the wisdom of the National Science Foundation in bootstrapping the development of such curricula.) Equally important, there are no consequential measures of impact, and thus no competitive pressures to improve educational effectiveness. The obvious contrast here is with consumer electronics devices, which are rated in magazines such as Consumer Reports: design and performance flaws will be noted in such magazines and must be corrected if the manufacturer expects sales. For the development of text series, however, teacher focus groups are a cost-effective proxy used by publishers for decision-making. If a group of teachers says they would buy the materials, why should a publisher invest in a lengthy materials refinement process?
A major constraint, not felt in the same way by academic researchers, is time. For those whose primary concern is getting a good product to market, the time spent reflecting on design with an eye toward codifying the knowledge that results from such reflections is a luxury that can rarely be afforded. The pressures on design houses differ in degree and perhaps somewhat in kind if the design houses have a somewhat academic orientation, but even so, there are few incentives for investigations toward the ER part of the spectrum. This is not to say that things must be this way. In fields such as engineering the creation of high quality, innovative products has top priority, along with theory building; and the codification of design knowledge is considered a beneficial subfield of engineering design (Schunn, 2008). Engineers in academia need both academic papers and prototype products to advance. In addition, publications in engineering journals help career advancement in industry as well. (As an extreme case, consider Bell Labs, which produced a significant number of Nobel Prize winners.)
Part of the reason for the current ER/EDD divide is the question of what is/should be researched, and how it feeds into the work of the person or group doing the research. Much academic research appears either too broad or too narrow for direct application in practice. Basic research that addresses fundamental mechanisms of learning tends to provide very general guidelines about what one ought to attend to in instruction. As a case in point, the problem solving research literature made it clear that a person’s knowledge, access to problem solving strategies, metacognition, and beliefs are all centrally important determinants of that person’s problem-solving success or failure (see, e.g., Schoenfeld, 1985). However, being aware of such general information provides little by way of direct guidance for a designer planning to construct a third grade “problem solving unit” – the information is far too broad for specific applications. In contrast, other research, having to do with students’ coming to grips with particular content, is often far too narrow for designers to use. Consider, for example, the literature on students’ systematic errors or “bugs” in arithmetic (e.g., Brown & Burton, 1978). Knowing how and why a student forms a particular “bug,” or knowing that there are 38 primitive bugs and more than 500 composite bugs, is at a level of detail designers don’t need to know.[3]
Conversely, those in the EDD community are primarily interested in the question of whether their particular intervention works, and how to improve it. This is typically a question of evaluation, which, on its own, tends to be of too narrow interest to attract most researchers – the question of interest to the research community being to understand how and why something works (if it does). Hence the research questions of primary interest to the EDD community often fail to draw the interest of the ER community, and hence bring little academic credit.
As noted above, design experiments – which are intended to support the development and examination of productive instructional interventions – may well be a site for productive contributions from both communities. The products of well conducted design experiments are improved interventions and improved understandings of the processes that result in their productiveness, and are thus meaningful contributions to the ER and EDD communities (Cobb et al., 2003; Schoenfeld, 2006). However, for a range of reasons, few design experiments carry the development far enough to produce robust, well-engineered products that are widely available to the potential user community (see Burkhardt 2006).
There is a class of research activities that is potentially of significant value to the designer community. This work concerns the delineation of productive design practices – the things that accomplished designers do, that lead to high quality designs. As I will argue later in greater detail, the educational design community, unlike the engineering design community (cf. Schunn, 2008), has not had a great deal of time or energy to codify principles and practices that lead to high quality design. As a result, there does not exist a common body of knowledge that can be used to bootstrap aspiring designers into the profession. Exploring such issues could be a very exciting research issue – unpacking expertise in novel domains is a respected research tradition – and the findings, as well as adding to the body of knowledge valued by researchers, could help codify the knowledge base for the educational design community.
In sum, there is good reason for a rapprochement between the ER and EDD communities, but a number of cultural obstacles to it. In the next section I describe the idea of professional vision, a possible mechanism for rapprochement. I will argue that the elaboration of designers’ professional vision will be of interest to the design community as a mechanism for codifying productive practices, and for researchers as an arena for the study of expertise.
Professional Vision
4In a later paper, Goodwin (1996) presents a photograph of the normal chaos in the operations room of an airport control office, in which airport personnel keep track of ongoing activities by scanning a broad array of TV monitors. What I see is largely uninterpretable, snapshots of activities that are as meaningless to me as the x-ray scans of my computer backpack as it goes through the airport security station. However, the airport personnel in Goodwin’s article are quick to pick up on a mishap (a runway canopy has slopped over the entryway into an airplane), quickly differentiating what is “normal” from what is not. Similarly, I hope the security people can distinguish the normal jumble of electronic equipment revealed in the X-ray of my backpack from an abnormal pattern that signifies danger.
Indeed, as anyone who has tried to “read” one will recognize, X-rays and their more sophisticated cousins, MRIs, provide perfect examples of the nature and scope of professional vision. The medical practitioner with a trained eye will either see or deduce the existence of things that go completely unnoticed by non-specialists.
Of course, one need not go outside the field of educational design to see professional vision at work. Consider the concept of slope. Ask a mathematician what happens as the positive slope of a line increases, and the answer will be something like his: “the graph of the equation y = mx + b is a line whose y-intercept is the point (0,b). Increasing the slope results in a line that also passes through (0,b) but is closer to vertical than the original line.” But, that is a learned understanding. What newcomers to a discipline see can be very different from what experienced practitioners perceive.
In the mid-1980s my research group was designing graphing software that, among other things, allowed students to graph functions by typing in their equations. One of my graduate students, Susan Magidson, built a “guided discovery” activity, in which she asked students to pursue the activities in Figure 2:
Figure 2: A “guided discovery” task
Clear the screen and type in these equations, one at a time.
y = 2x + 1
y = 3x + 1
y = 4x + 1What do you notice?
What stays the same?
What changes?
What do you think will happen if you type in y = 5 x + 1?Sketch your prediction on this empty graph [given below in the original] and then try it on the computer.
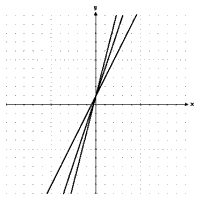
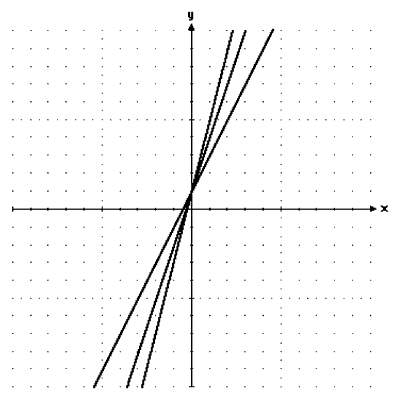
Magidson expected the students to see what she saw – that all the graphs of the form y = mx + 1 are straight lines, they all pass through the point (0,1); and, as m increases, the lines get steeper.
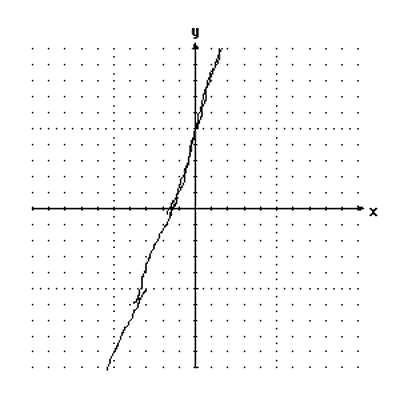
The graphs looked as one would expect: see Figure 3. However, the student responses were not at all what she expected. Here are the verbatim responses from one pair of students:
What do you notice? The higher the number you are multiplying by x the more upright the line.
How are these lines similar? All practically the same angle.
How are they different? They're not the same angle.
What do you think will happen if
you type in y = 5x+1?
Sketch your prediction on this empty graph and then try it on the
computer. [The student sketch is given in Figure 4.]
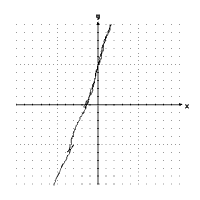
What happened? It went more upright than the other lines but less upright than we thought it would be.
Note that the students’ graph passes through the point (0,5) – they had failed to note the common point of intersection! Similarly, other students had attended more to artifactual features of the graphing process than to the features we consider mathematically central.
The answers students gave Magidson were typically like these:
What do you notice? The lines get more jagged when we type in higher numbers.
What stays the same? They all move from the left to the right.
[The software graphed functions from left to right. In the case of the
lines graphed, this meant the lines appeared to be generated moving
upwards to the right.]
What changes? They start further to the right when we type in a bigger number.
What do you think will happen if you type in y = 5x + 1? It will be more jagged and start further to the right.
In short, some things that Magidson considered trivially obvious, such as the fact that all of the lines intersected at the point (0,1), went unnoticed by many students; and some things she thought could be safely ignored, such as the ways the lines traversed the screen, grabbed the students’ attention. The students needed to learn to see the way she did. Such things don’t just come naturally. (See Stevens & Hall, 1998; see also Lobato, Ellis, & Muñoz, 2003.)
When Magidson shared her findings with our community another student, Michael Jay, suggested that she try something different. The result, after some tinkering, was the “Starburst” task in Figure 5. Students had access to the same software for this task that they had for her earlier curricular activity.

Can You Make a Starburst?!
Here’s how:
Type in the equation y =  x but with a
number in place of the
x but with a
number in place of the  .
.
Hit the return key. There’s the first line in your starburst.
Try another number. Now you’ve got two lines.
Keep trying different numbers until your starburst looks like the
one in the picture.
Good luck!
Students’ engagement with this task was very different than with the guided discovery task. Typically students typed in y = 1x, y = 2x, y = 3x, and a few more. They noticed that the lines were getting steeper as they typed in larger coefficients. This was useful when they tried to fill in the top-right-and-bottom-left of the starburst, but it left them in trouble when they wanted to fill in the rest. Faced with the inadequacy of the counting numbers as coefficients, some students tried fractions of the form 1/n or decimals as coefficients; others tried negative numbers. To make a long story short, what the students found salient, and what they attended to, was a function of their goal-oriented behavior. The design challenge, then, was to craft activities that resulted in the students’ attending to the things that mattered mathematically. This is a design principle, of course, one that Magidson learned as she produced her dissertation (Magidson, 2003; see also Moschkovich, Schoenfeld, & Arcavi, 1993).
Finally, I note that professional vision applies to perceptions of activities as well as to perceptions of things. Some years ago David Berliner (1988, 1989) showed beginning and established teachers quick views of classroom scenes. Generally speaking, the beginners got a global overview of the activities, and suggested generic things the teacher might try. In contrast, more experienced teachers made much more fine-grained observations and accordingly targeted suggestions – comments of the type “the kids at table 3 are bored but on task. The kids at table 4 are engaged, and the teacher doesn’t have to worry about either group. But if the teacher doesn’t intervene at table 2 soon, things will get out of hand. They’re off task and starting to get rambunctious.”
In short, there is a face value case that there are forms of professional vision relevant to every aspect of instructional materials design and its implementation – the design of meaningful and engaging activities, the creation of tasks (and units of curriculum) that focus on key mathematical ideas, the assessment of the ways activities play out in the classroom, and the assessment of student understanding. Such professional vision is a potentially significant resource that has barely been tapped. The concluding section of this paper makes a proposal for tapping it.
A Modest Proposal
5The development of expertise takes time. No matter what the field – becoming a chess master, a professional musician, an expert electronics technician, computer programmer, educational researcher, or educational designer – the standard figure is that it takes on the order of 10,000 hours of work in a field for a beginner to develop the skills of an established professional (see, e.g., Ericsson & Smith, 1991). Much of this is done on an individual basis, by way of apprenticeship, practice, and reflection. However, different fields offer different kinds of collective support structures for the development of expertise. Educational research and educational design and development differ substantially along this dimension.
With rare exceptions – one of which is being institutionalized in this journal, as the series “A designer speaks”– educational designers have few incentives to codify their reflections on their practices and present them publicly.
Research apprenticeships and the production of research typically result in three different kinds of products:
- skilled practitioners (educational researchers);
- additions to the corpus of scholarly knowledge – the products of research;
- additions to the corpus of scholarly craft knowledge, the means by which research is produced.
Contributions to this third category take place in at least two ways. First, the papers typically published in research journals contain methods sections. In the best of all possible worlds, these methods sections allow other researchers to replicate and extend the work described in the paper. Often this is not the case, both because methods sections are not always as good as they should be and because research itself is (rather like design) partly an art form, not all aspects of which can be distilled onto paper. However, the fact is that there is a formal mechanism, in research papers, for the distillation of scholarly craft knowledge, which can help readers profit from the experiences of other researchers. Second, educational research has a tradition of producing methods handbooks that are explicitly focused on capturing the processes by which research is conducted. Aspiring researchers (and established professionals!) thus have access to community-developed resources to support their continuing development as researchers.
Apprenticeship into the design and development community typically results in analogs to the first two of these categories. That is, apprenticeship in EDD typically produces
- skilled practitioners (educational designers and developers);
- additions to the corpus of well-developed materials – the products of design and development.
Broadly speaking, the EDD community does not produce an analog to the third research product. That is, the EDD community has not had communal mechanisms for codifying design craft knowledge,[4] the means by which educational design and development are produced. A polished piece of design is often something to admire and emulate, but the very act of polishing often obscures the process of refinement. Moreover, there exist neither “educational design methods” handbooks nor, with exceptions such as the nascent “designer speaks” series in this journal, public reflections on the part of educational designers. (Indeed, ISDDE and Educational Designer were created to make progress on this and related fronts.)
Broadly speaking, neither members of the educational design and development community nor educational researchers have made an active study of educational design. To give but one example: when Susan Magidson was writing her dissertation, she contacted the authors of the then in-process NSF-supported curricula, asking if they had documented their design processes in the past or were planning to do so. The responses were consistently “no” – not because the designers thought the idea was uninteresting but because they were, in essence, on a design treadmill. Given the time pressures on, and the reward structure for, designers, their lives didn’t allow the time for such public reflection. (Indeed, the first contributor to the “designer speaks” series, Malcolm Swan, is both a designer and a researcher, so he will get “credit” for his piece in ways that non-academics would not.)
My proposal is intended to address this lack. It has a general and a specific part. Broadly speaking, I believe that a collaborative program of Research-and-Design explicating educational designers’ knowledge base(s), including their professional vision(s), would be both doable and a great deal of fun. The challenge is to document accomplished designers’ core knowledge, to understand what shapes their behavior, what they perceive (the vision thing!), and how that knowledge and those perceptions guide their design actions (e.g., revisions).
To indicate the potential value of the enterprise, let me point to some of the insights in Swan (2008), and to the value of systematizing inquiries that could yield similar insights.
Swan presents and illustrates a theoretical framework, general design principles, and a discussion of some revisions he made after embarking on classroom trials. Consider, for example, Swan’s introduction:
“This paper describes some of the research-based principles that I use when designing learning experiences to foster conceptual understanding. These principles are illustrated through the discussion of one type of experience: that of sorting multiple representations. I refer to learning experiences rather than tasks, because tasks are only one component of the design. Close attention is also paid to the role of the teacher in creating an appropriate climate for learning to take place.” (Swan, 2008. Emphasis added.)
This perspective, though seemingly simple, is critically important. Further detail offered by Swan, in which he discusses the needed transition for teachers from a “transmission” orientation to a “collaborative” orientation, perfectly encapsulates Magidson’s (2003) hard-earned knowledge, as she made the transition from developing “guided discovery” materials in which the students failed to attend to what was mathematically central to setting a design challenge in which the students’ purposeful activities, properly facilitated by the teacher, led to productive mathematical engagement with the desired concepts.
There is a long story here, which I shall condense. Magidson refined the starburst activity and piloted (trialed) it in courses she taught. She then offered the activity to a collaborating teacher, who proceeded to take the challenge out of the task – he told the students that the goal was to replicate the starburst precisely, and then gave them an algorithm for doing so! [5] Subsequent iterations of the task contained information for the teachers about how to frame the task so that the students had the latitude to engage productively with it. Swan rightly flags the challenge in helping teachers make the shift in orientation (and, in corresponding goals for classroom activities).
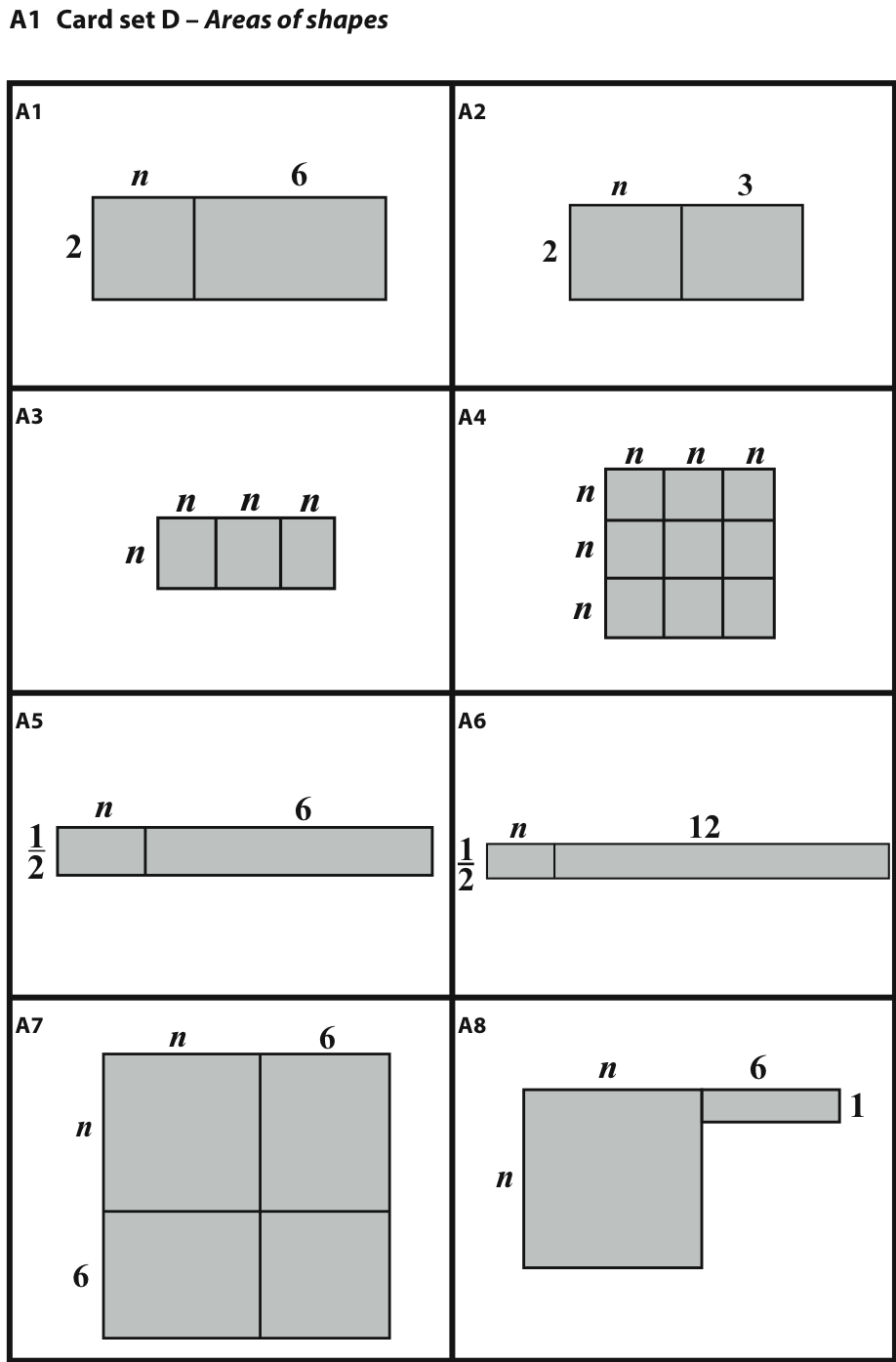
One of the tasks Swan (2008) discusses is a card-sorting task in which students are asked to make piles of cards in which equivalent expressions (e.g., 2(x+3) and 2x+6) are found. In his paper, Swan shows the first version of his task materials, which is reproduced as Figures 6a and 6b, and the final version (published by DfES, 2005), given as Figure 7.
A number of design changes are apparent. Among the most interesting to me are the blank cards in the collections of algebraic representations and written explanations. Swan comments,
“The original version contained no blank cards. This led students to match the final few expressions using elimination strategies. On reflection it appeared much more profitable to encourage students to devise cards of their own. In addition, some spaces were left on the tables cards, partly to encourage students to engage in substitution and also so that matching would be less easy to spot. Interestingly, the tables now make it possible to use new strategies for matching. For example, students who recognised square numbers in the table could search for a square area. Students were also surprised to discover that several expressions could correspond to the same table.” (Swan, 2008)
This paragraph makes clear aspects of Swan’s professional vision, both in terms of design (leaving blank spaces in the tables to encourage substitution) and in terms of his focus on student process rather than merely the products of their work. As he watched students engaging with the task, he noticed when they essentially stopped thinking – matching the few cards left in a collection, for example. He then included blank cards in the collection, both to make the matching task less mechanical and to enable the students to generate new algebraic expressions, which would provide deeper insight into their algebraic thinking.

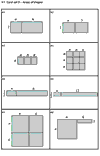
This page invites students to interpret the meanings of algebraic expressions. They then search for expressions which are equivalent, by substituting n = 4 into each one.
You will need to emphasize that expressions are only equivalent
if they give the same answer for every possible substitution.
If possible, introduce this as a card sorting activity. (A photocopiable
sheet is included on the next page.)
Card sorting frees the students from having to write and enables
them to pay more attention to the meanings of expressions.
When they have finished arranging and rearranging the cards, they may
then like to make a permanent copy by pasting their arrangement onto a
large sheet of paper.
As students sort the expressions, listen carefully and note their difficulties.
This page looks again at the same expressions, but this time links them to areas. This should help students to begin to see why different expressions are equivalent.
Ask students to match the expressions on the cards with the
shapes.
Encourage those that finish to invent additional expressions for each
shape.
Leave time for students to make notes on the important things they feel they have learned. When they have done this, ask some to read aloud what they have written and invite questions and comments from other members of the class.
| Figure 7: Cards for matching (Swan, 2008 - originally from "Improving Learning in Mathematics" DfES, 2005) | |||
|---|---|---|---|
| Figure 7: Cards for matching (Swan, 2008 - originally from "Improving Learning in Mathematics" DfES 2008) | |||
|---|---|---|---|
 |
 |
||
 |
 |
||
Here is my general proposal. Imagine a researcher-designer partnership, perhaps Schoenfeld with Swan, or the pairing of any observationally oriented researcher with a willing and talented designer. (Of course, some overlap in perspective between the two is of importance – there is always an issue of communicating values and ideas effectively between people with somewhat different orientations.)The researcher works with the designer, as participant-observer in the design process. (Or, the researcher apprentices to the designer, if this can be done without too much damage to the design process!) The researcher’s documentation task includes noting initial designs, videotaping the various trials of the materials, recording the evolution of the designs at each stage, and interviewing the designer about the reasons for all of the changes. The main focus of such a research program would be to address the following two large questions:
- How and why do experienced designers make the (tacitly principled) decisions they do, as they undertake design and revisions?
- What orientations and goals shape their decision-making?
- What is the knowledge base – including design principles and techniques, heuristics, and professional vision – that supports such decision-making?
By way of gedanken-experiment, imagine that a researcher had been present with Malcolm Swan when he was trying out his first set of card sort materials (Figure 6a and 6b). A sympathetic listener would serve as a sort of sounding board. I can imagine Malcolm saying something like, “Did you see what they just did? They used elimination at the end, they didn’t really think about the mathematics involved. I’ve got to do something about that,” with the subsequent conversation generating possible ways to address the issue. That kind of conversation would serve the dual purpose of helping the designer think through design challenges and allowing the researcher to unpack the designer’s professional vision. Often such things, once noted, can become design heuristics and can be recognized and used by others.
Of course, such things can and should be systematized. One can imagine a research protocol for collaborative work with designers, including the descriptions of the kinds of activities that turn out to be productive for both the researcher and designer – e.g., a “sounding board” partnership rather than “shadowing,” the use of post-piloting interviews – “Just what were you looking for? Why is this paper (or video clip) evidence of its presence (or absence)? What can be done to move the students in the direction you want?” – and so on.
If all goes well, this kind of agenda would be equally valuable to researchers and designers, both individually and collectively. At the individual level, skilled designers are sure to profit from the explication of their often tacit skills, and they may well be prompted to think more deeply about them. The presence of a sympathetic other can help one to “think out loud” and, at times, more creatively. Moreover, there is value to the designer in codifying what he or she knows. (By way of parallel, there are many reasons that skilled musicians give master classes. Bringing along the next generation is one, but explication of and reflection on one’s own work is also a tangible benefit.) There are multiple benefits to the individual researcher as well. The researcher partner will expand his or her design repertoire – something that has always been of use to me during my career, though I claim no expertise. The research publications themselves will be of significant interest, both as general contributions to the literature on expertise and more specifically as the elaboration of competency in an obviously relevant and important domain. (I think of this kind of work as being analogous, in some sense, to the unpacking of problem solving proficiency in mathematics and science.) Those researchers who pursue this kind of work may become exemplars of a new kind of hybrid professional, who possess two sets of synergistic skills.
At the collective level, this joint research-and-design agenda should be useful to:
- Designers:
- Codifying the craft would help generate the next generation. At present there is not an adequate supply of designers, and, as noted above, there are precious few public mechanisms by which designers can profit from the process knowledge of other designers. As Schunn (2008) argues, larger fields such as engineering have codified design, and this has made the processes of design more efficient. Educational designers could profit similarly. It would be nice, for example, to have a volume of systematically organized contributions from designers (as in the “designer speaks” series in this journal) and researchers, individually and in partnership, that designers could use as a reference. Ultimately, a Handbook of Educational Design could systematize such contributions.
- Researchers:
- At present, codifying designers’ knowledge, goals, and orientations is near-virgin research territory. Mapping out that territory is not only an interesting and valuable intellectual challenge, but – because this is a new area – those who make the first significant inroads into it will also be serving their careers well. In addition, those researchers who employ design in their work will profit from insights into design. To the degree that productive design principles become codified and accessible to researchers, the interventions designed by researchers will improve, and thus the research itself will be better.
- The world at large:
- If such work can support the development of more and improved educational materials, then the consumers of such materials – which at some point in their lives, is everyone – are the ultimate beneficiaries.
In sum, the large research agenda seems well worth pursuing. There are, I suspect, a number of ways the agenda might be pursued. Some of the better-known design houses, worldwide, are located with researchers in close proximity, and some individuals actually play dual roles as researchers and designers. Some do, of course, as I noted in the opening paragraphs of this article. My hope is that the practice will become more common than it is now.
In addition, there is the possibility of supporting such work in a systemic way. I close with mention of a more focused proposal that Chris Schunn, Elizabeth Stage, Frank Davis and I are in the process of conceptualizing. It seems to us that a research training grant, in which university researchers team up in partnership with well-regarded design houses, could well spawn the kind of research discussed here. Research mentors could supervise graduate students who interned in the design houses, apprenticing to design projects while being members of research groups that analyzed the design process in an ongoing way. The graduate students’ dissertations, which would be situated at the intersection of educational design and research, could take various directions, e.g.,
- Chronicling the evolution of a design and the ways in which piloting (and the professional vision that supported it) shaped that evolution. This could give rise to the codification of a range of design heuristics as well as descriptions of the underlying design principles that proved to be productive.
- Documenting “developmental trajectories” of designers. Are there typical pathways into the profession? Are there ways that essential skills can be catalyzed?
- Unpacking the ways in which various aspects of design contributed to the final products. Ultimately this might help to provide top-level views of the design process, checklists of fail-safes during the design process, etc.
- Focusing specifically on the knowledge (including design principles and techniques, heuristics, and professional vision), goals and orientations of experienced designers, and unpacking the ways in which they work.
Such work would contribute to both fields and to the larger agenda described above.
Acknowledgments
6Crafting a paper that is intended to reflect perspectives from two only partially overlapping intellectual communities and subjecting it to the friendly refining fire of both groups has brought to life some of the challenges and rewards of “boundary crossing.” I would like to express my sincere gratitude to Paul Black, Hugh Burkhardt, Christian Schunn, Elizabeth Stage, Malcolm Swan, and members of the Functions Group at Berkeley for exchanges that problematized for me a number of issues discussed in this paper, and that resulted in my thinking more deeply about them than I otherwise would have.
References
7Goodwin, C. (in press). Things and Their Embodied Environments. In L. Malafouris and C. Renfrew (Eds.), The cognitive life of things. Cambridge, U.K.: McDonald Institute Monographs.
Henningsen, M., & Stein, M.K (1997). Mathematical tasks and student cognition: Classroom-based factors that support and inhibit high-level mathematical thinking and reasoning. Journal for Research in Mathematics Education, 28(5), 524-549.
Lobato, J., Ellis, A., & Muñoz, R. (2003). How “focusing phenomena” in the instructional environment support individual students’ generalizations. Mathematical Thinking and Learning, 5(1), 1-36.
Moschkovich, J., Schoenfeld, A. H., & Arcavi, A. A. (1993). Aspects of Understanding: On Multiple Perspectives and Representations of Linear Relations, and Connections Among Them. In T. Romberg, E. Fennema, & T. Carpenter (Eds.), Integrating research on the graphical representation of function, pp. 69-100. Hillsdale, NJ: Erlbaum.
Schunn, C. (2008). Engineering Educational Design. Educational Designer, 1(1). Retrieved from www.educationaldesigner.org/ed/volume1/issue1/article2 September 1, 2008
Senk, S. L., & Thompson, D. R. (Eds.) (2002) Standards-based school mathematics curricula: What are they? What do students learn? Mahwah, NJ: Erlbaum.
Stein, M.K, Grover, B.W., & Henningsen, M. (1996). Building student capacity for mathematical thinking and reasoning: An analysis of mathematical tasks used in reform classrooms. American Educational Research Journal, 33(2), 455-488.
Stevens, R. & Hall, R. (1998). Disciplined perception: Learning to see in technoscience. In M. Lampert & M. L. Blunk (Eds.), Talking mathematics in school: Studies of teaching and learning (pp. 107-149). Cambridge: Cambridge University Press.
Swan, M. (2008). A Designer Speaks: Malcolm Swan. Educational Designer, 1(1). Retrieved from www.educationaldesigner.org/ed/volume1/issue1/article3 on September 1 2008.
Footnotes
[1] Note that the question of how something is working – a focus on what students experience and how their understandings change as a result – is different from the question of whether something is working. It goes without saying that the developers of the NSF curricula had a vested interest in demonstrating that their curricula were effective; see, e.g., Senk & Thompson (2003) for a collection of such reports.
[2] As Paul Black has pointed out, the phrase “make a difference” is ambiguous. It might, for example, mean “enable students to master a particular body of content more efficiently.” It might mean “enabling students to become better problem solvers.” It might mean “enable students to become more reflective and better learners.” Or, it might mean “support the development of a community of learners.” What follows can be read with any and all of those interpretations in mind.
[3] There is, of course, a large body of work under the aegis “research into practice,” which aims to make research findings digestible for practitioners (mostly teachers). I honestly don’t know how useful the design community finds such work; if it is used extensively, that is a sign of this researcher’s ignorance.
[4] Frank Davis and Elizabeth Stage have pointed out that the phrase “design craft knowledge,” which I chose to parallel “scholarly craft knowledge,” may do a disservice to the design community. The skills developed by designers are complex and demanding - as noted above, design experts, like other experts, take on the order of 10,000 hours to develop their expertise. Such expertise includes having a particular kind of philosophical orientation toward the work, a commitment to reflection, and a commitment to the improvement of practice and the enrichment of the community of practitioners. Through the years there have been “on paper” contributions to this agenda, e.g., in TERC’s publication Hands On. My hope is to catalyze more such efforts and systematize them. I would no more reduce “expertise in design” to producing materials than I would reduce “expertise in research” to producing research findings.
[5] Today, of course, the understanding that teachers tend to simplify tasks for students (at least when students have difficulty with them) is well known; see Henningsen & Stein, 1997; Stein, Grover & Henningsen, 1996). Magidson’s hard-earned knowledge came in 1992, before these findings were known.
About the Author
8Alan Schoenfeld is the Elizabeth and Edward Conner Professor of Education and Affiliated Professor of Mathematics at the University of California, Berkeley. He is a Fellow of the American Association for the Advancement of Science and the American Educational Research Association, and a Laureate of the education honor society Kappa Delta Pi. He has been President of the American Educational Research Association and the vice president of the National Academy of Education. In 2008 he was given the Senior Scholar Award by AERA’s Special Interest Group for Research in Mathematics Education.
A main focus of Schoenfeld’s work has been problem solving. He has organized projects that produce mathematics assessments and that foster teachers’ professional development; he served as a Principal Investigator of the Diversity in Mathematics Education project. Schoenfeld is concerned with finding productive mechanisms for systemic change and for deepening the connections between educational research and practice. His current work, focusing on understanding productive mathematics teaching, is grounded in twenty years’ work on the construction of an analytic model of teachers’ decision-making.
Schoenfeld was lead author for grades 9-12 of the National Council of Teachers of Mathematics’ Principles and Standards for School Mathematics. He was one of the founding editors of Research in Collegiate Mathematics Education, and has been associate editor of Cognition and Instruction. He has written, edited, or co-edited twenty-one books and more than a hundred and fifty articles on thinking and learning.
In Response
9November 2009: Paul Black has written a response to this article : see Black, P. (2009) In Response To: Alan Schoenfeld. Educational Designer, 1(3).2 - available at at http://www.educationaldesigner.org/ed/volume1/issue3/article12