The author of any mathematics textbook or teacher resource book has a twin audience in the classroom – the learner of mathematics and the mathematics teacher – and the pedagogical and mathematical choices behind the writing will have effects on both parties. Some parts of a teacher resource book are entirely teacher-facing, offering explicit advice or direction about how the teacher might conduct the lesson, but even those parts (e.g., task sheets) that address the learner directly never quite lose sight of the fact that the teacher is ‘looking over the learner’s shoulder’. The questions and prompts aimed at learners can communicate implicit pedagogical messages to the teacher about what is valued and the ways of working that are being encouraged. For example, see Cake-Cutting contest (Figure 1)

The Convergent–Divergent Model
An opportunity for teacher–learner development through principled task design
Colin Foster
Centre for Research in Mathematics Education,
School of Education, University of Nottingham, UK
Abstract
iThe tasks that mathematics teachers are invited to use in their classrooms have profound effects not just on the learners who do them but also on the teachers themselves. This paper introduces the Convergent–Divergent Model (CDM) for the design of mathematical tasks. The CDM consists of two distinct phases: the first, a convergent problem-solving episode, and the second, a more divergent, open-ended, exploratory part. The two-phase design is built on twin intentions both for the mathematical growth of the learner and for the pedagogical development of the teacher. The principles of design employed in this model are elucidated through descriptions of the construction of several examples of such tasks in published mathematics teacher resource books written by the author.
1. Introduction
1There is little doubt that textbooks still predominate in the teaching of mathematics in schools, at least in the UK. Professional associations such as the Association of Teachers of Mathematics (www.atm.org.uk) have for a long time been publishing alternative resources containing rich, open-ended investigative tasks that are in line with their philosophy (e.g., Ollerton, 2002), but on the whole these risk serving mainly a niche market of like-minded practitioners. However, more recently there have been encouraging informal indications that alternatives to textbooks are gaining increasing mainstream status and being viewed with less suspicion by commercial publishers. Conventional publishers are showing a growing interest in commissioning text-based materials, unrelated to textbook schemes, consisting of lesson ideas for mathematics teachers. Although such teacher resource books are less commercially important, being purchased on a one-per-school or one-per-teacher basis, rather than one-per-learner, and mainly supplement rather than supplant reliance on textbooks, they may nevertheless be seen as an opportunity for developing teachers’ practices and enhancing the diet offered to learners of mathematics. It might be hoped that some schools currently facing unprecedented financial pressures on resources might opt for mainly or exclusively non-textbook ways of working, and resources such as these could become increasingly relevant.
I have published many such books of resource materials for teachers (e.g., Foster, 2012a, 2012b, 2012c, 2011a, 2010, 2009, 2008a, 2008b), as well as numerous articles in teacher journals, magazines and the mainstream educational press. In all of my writing, I operate from a constructivist perspective on learning (von Glasersfeld, 1995) and seek to offer learners open-ended, exploratory mathematical tasks which provide rich opportunities for building conceptual understanding alongside developing procedural fluency (Foster, 2013a). In the notes for the teacher, I attempt to encourage sociomathematical classroom norms (Yackel and Cobb, 1996) such as a valuing of independent collaborative small-group work and a determination to take seriously learners’ ideas (Foster, 2013b). In this paper, I position myself as a self-critical designer, teacher and researcher. I am committed to attempting to exploit the opportunities presented by these recent developments to improve the teaching of mathematics in schools through the provision of materials based on richer and more diverse mathematical tasks.
Figure 1: Cake-Cutting Contest
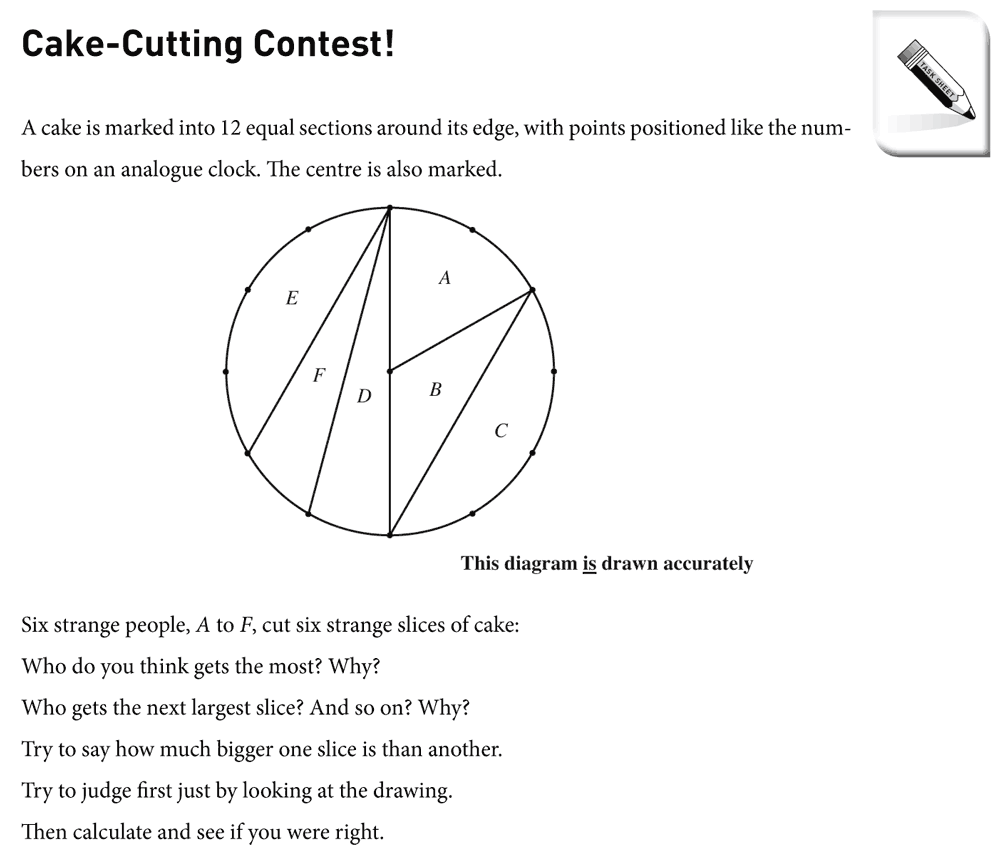
In Cake-Cutting Contest!, the prompts on the learner task sheet, ‘Try to judge first just by looking at the drawing. Then calculate and see if you were right.’ are intended to promote a conjecturing climate within the classroom in which learners develop provisional hypotheses as they work, which they later evaluate. This could become a classroom norm which might operate in other situations. Similarly, the prompt, ‘Invent another crazy cake-cutting contest like this in which some of the slices look about the same size. Work out which are actually bigger.’ is intended to give responsibility to learners to construct problems and take control and ownership over the details of mathematical tasks
Although the cake is in the shape of an ordinary right cylinder, only a few of the cuts go from the centre, so learners need to use their knowledge of sectors and segments of circles to find the areas, some of which come out quite close, and two of which are the same. Although learners might use informal and intuitive methods to order some of the slices, they cannot determine that two slices have exactly the same area without doing some precise mathematics.
The conclusion of the convergent phase is the ordering of the slices by area. Then, for the divergent phase, learners have the opportunity to devise their own similar problem:
Invent another crazy cake-cutting contest like this in which some of the slices look about the same size. Work out which are actually bigger.
This more open task affords the opportunity for learners to self-differentiate, according to what they are comfortable with, using sectors and/or segments of various sizes, or perhaps even using a non-circular cake. A classroom culture that supports finding ‘interesting’ or surprising examples, rather than the simplest solution possible, is beneficial here.
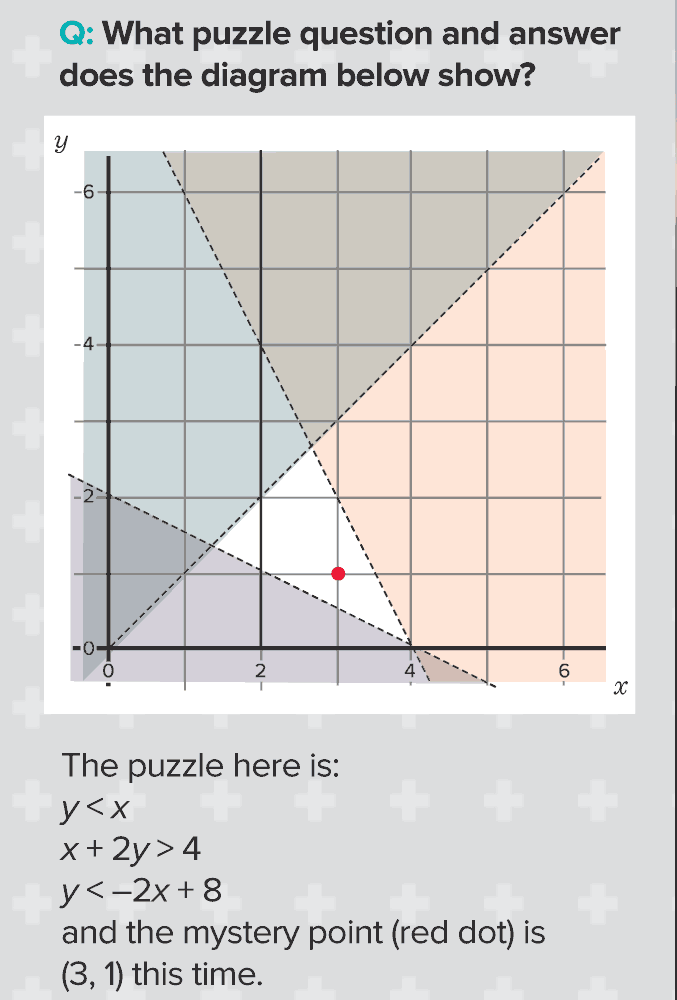
Designing resources for use by unknown colleagues entails numerous compromises: there is no value in writing resources that are so idiosyncratic that they could only realistically be used by the author, or someone with a very similar outlook; on the other hand, excessively ‘safe’ materials that might easily be ‘delivered’ by a non-specialist teacher may not adequately embody the author’s educational values. Consequently, there is a desire to produce materials that will provide some degree of challenge to a more traditional mathematics teacher, so as to inspire them to risk moving away from their habitual practice. However, the disturbance created must not be so much as to be intimidating and to risk the resource being written off as ‘impractical’. Informal feedback and discussions with publishers have suggested the need for ‘safe’ beginnings to tasks, which teachers feel are achievable. In a similar way, learners who are not used to working in more open-ended ways may be turned off by sudden requests to work in a creative and exploratory manner. However, once drawn in to the task and ‘hooked’, the learner may be prepared to risk responding to some more adventurous prompts offered later on, and the teacher may be prepared to go along with this if the learners are not objecting too vociferously! For example, see Shading Graphical Inequalities (Figure 2)
In this paper, I consider a mathematical ‘task’ to be any question or prompt which provokes mathematical thought, reserving the word ‘activity’ for the process of learners working on the task (Christiansen and Walther, 1986). I introduce here one model for task design, which I call the Convergent–Divergent Model (CDM). The principles and rationale underlying its structure will be described, followed by examples of tasks employing that model that I have written in published teacher resource books. Some concluding remarks will be made regarding how this work may be taken forward.
Figure 2: Shading Graphical Inequalities
 Click here to see the full lesson plan.
Click here to see the full lesson plan.
This is a task with a traditional and ‘safe’ beginning but which concludes with an invitation for learners to problem pose creatively.
Learners will be used to mathematical versions of games like ‘20 Questions’, where the aim is to identify the object that someone is thinking of. For example, the teacher might say, ‘I’m thinking of a number ...’ and the learners have to find out what the number is. In this lesson, the teacher is thinking of a point, which is represented by a pair of coordinates. This leads to some work on simultaneous linear inequalities.
The full lesson plan is available from www.teachsecondary.com.
The full lesson plan is available online from: www.teachsecondary.com/maths-and-science/view/lesson-plan-ks4-mathematics-shading-graphical-inequalities
Another example, highest common factor/lowest common multiple this time with multiple open concluding tasks, is available here.
Another example, highest common factor/lowest common multiple this time with multiple open concluding tasks, is available from: http://www.teachsecondary.com/maths-and-science/view/lesson-plan-ks4-mathematics-highest-common-factor-lowest-common-multiple.
2. The importance of the teacher’s perspective in designing tasks
2The lesson to be analysed is Pizza slices (Foster, 2011a: 98–101; Figure 3). This lesson was not developed through a research-based process of trialing, but was refined out of experiences gained with the task in my own classroom. In the analysis given below, I draw distinctions between the way in which I used the task, as a teacher with my own classes, and how I developed the published version, in order to elucidate the movements that took place during the design process.
Anecdotal evidence is compelling that mathematics teachers rarely have time to read fully the teachers’ notes sections of published resources – or if they do it is during the lesson rather than beforehand, perhaps just to check the answers. Consequently, I sought to make the learner task sheet (Figure 3) useable as a standalone resource, phrasing the questions such that they would make sense as an isolated task divorced from any wider context. However, in the teacher resource pages I offered a full lesson plan. In devising the material for this classroom resource, I saw my role as designer as going beyond pointing teachers to worthwhile tasks; I wanted to provide the classroom practitioner with viable plans for rich, coherent lessons.
The respective roles of designer and teacher are an area of considerable debate. For Wittmann (1998):
the design of substantial teaching units, and particularly of substantial curricula, is a most difficult task that must be carried out by the experts in the field. By no means can it be left to teachers, though teachers can certainly make important contributions within the framework of design provided by experts, particularly when they are members of or in close connection with a research team. (p. 96)
He prefers to see the teacher as the director, rather than the writer, of the play. However, this does not necessarily mean that the teacher’s contribution to the details of the lesson is minimal. When Lodge (2011a: p207) reflects on the relationship between the writer and director of a television play, he feels that ‘if there isn’t a certain amount of friction between them then the result will be uninspired; some conflict and debate and mutual criticism is healthy’. He mentions that writers who do a lot of television work often want to direct their own work, but points to the danger of ‘losing the creative tension of collaboration’ (p207). It would seem perhaps that the challenge for the lesson designer is to provide a detailed enough plan to guide the teacher in an effective direction without being so rigid that the only way that the teacher can exercise any individuality is to reject the task completely and do something else instead. A helpful way forward is Burkhardt’s (2008) notion of appropriate ‘design load’ to characterise the extent to which it is left to the teacher to make important design choices in the classroom milieu. Recognising the extreme time constraints under which mathematics teachers labour, I wanted to do as much of the essential planning work for the teacher as possible, yet without producing an inflexible and oppressive structure that teachers would end up battling against.
Stein, Grover and Henningsen (1996: p460) explored ‘the extent to which tasks can change their character once unleashed in real classroom settings’, and found that teachers had a tendency to make difficult tasks easier. In a similar vein, Sleep (2012: p936) bemoans the way that ‘teachers seem to miss the mathematical point of the task or lesson or have difficulty maintaining the mathematical focus once an activity is in motion with students’. Being aware of this danger, the designer is faced with the difficult task of providing enough teacher support to prevent ‘lethal mutations’ (Brown & Campione, 1996) of the task, which fundamentally undermine its effectiveness, while not hemming in the teacher so tightly that productive adaptations to the particular contingencies of the teacher’s own classroom – or brilliant ideas not envisaged by the designer – are ruled out. Bruner (1966: 166) comments that ‘Teachers can make or break materials by their attitude toward them and their pedagogical procedures’, yet rejects the notion of ‘teacherproof’ materials as ‘mischievous’.
Aware of these issues, I sought to create a tone of collegiality throughout the lesson plans that I designed, in which I viewed the teacher as a partner in the process of constructing the lesson. Consequently, I opted for the language of suggestion, rather than prescription, throughout the teacher notes pages, while seeking to exercise some measure of control over what I regarded as the essential elements of the tasks by providing ready-made photocopiable task sheets containing instructions directly addressing the learners.
3. Principles for mathematical task design
3I did not begin designing mathematical tasks in a principled fashion at all, although I did start with constructivist views (von Glasersfeld, 1995), based on my reading of the mathematics education literature, about the possible nature of mathematical activity and learning that I desired to provoke (Mason and Johnston-Wilder, 2006). Principles have emerged later on through looking back at the hundreds of tasks that I have developed and reflecting on my own experiences of using them in the classroom, along with numerous comments from critical colleagues. It is attention to these principles that has led to the development of the CDM, which is the subject of this paper. Feedback from trials would, of course, give detailed and reliable information to guide development, which is particularly important when designs are innovative, and thus outside the experience of commentators. However, there was little opportunity for such trials – other than informally among colleagues – in the design of the lessons described here, and this unfortunately places limits on how appropriateness for teachers and learners may be judged.
There are several well-established sets of design principles for mathematical tasks. Ahmed (1987: p20) offers a demanding set of criteria, listing 10 desirable features of a ‘rich mathematical activity’, including accessibility, extendibility, the potential for surprise, enjoyment and originality, and tendencies for learners to ask questions, discuss, make decisions, speculate, make hypotheses and prove. Other valuable and relevant design principles can be found underlying the construction of model-eliciting activities (Hamilton et al., 2008), which are real-world problem situations designed to be tackled by small groups of learners. Model-eliciting activities are based on six design principles, including connection with reality, explicit documentation of thinking and self-evaluation. These principles, many of which, like Ahmed’s, might be seen as criteria for features of the end products of design, set a high standard (see Swan, 2008). It seems to me that although a designer might aspire to do many of these things across a series of lessons, it may be expecting too much to try to achieve all of them in every single lesson.
Instead, I have chosen to draw out from my work just three key principles to guide future designs. These principles are formulated as desired features of the finished task, rather than strategies for achieving those ends. They have arisen as a distillation of elements that I have repeatedly sought to embody in tasks that have been judged by others as effective. My published materials have been reviewed, and I take their favourable reception, by mathematics education researchers as well as by classroom practitioners, as informal peer validation (reviews are available at www.foster77.co.uk/books.htm). Arising from this work, three principles emerge for consideration.
A mathematical task should be:
3.1 Enticing
The introduction to the task should have some immediate appeal to learners, perhaps by posing something counterintuitive, paradoxical or provocative, so that a resolution or response needs to be actively sought. A problem that is manifestly ‘problematic’ in some way is more likely to entice learners into devoting their energies into making sense of the situation. As Ollerton and Watson (2001: p57) advise, ‘a good starting task should intrigue and motivate students and lead them to a rich network of mathematical concepts and techniques’. There are parallels to draw on here with how a story or film engages and maintains the reader’s or viewer’s interest and involvement. According to Lodge (2011b: 14), a literary narrative ‘holds the interest of an audience by raising questions in their minds, and delaying the answers’. Likewise, a good enticing task raises mathematical questions, either explicitly or by provoking learners to ask those questions – and the answers are delayed until learners reach them for themselves.
One common way in which a task can be effective in capturing learners’ interest at the outset is for there to be some connection with ‘their world’. However, such ‘relevance’ is not essential, and my experience with these tasks suggests that purely mathematical starting points can be just as effective with a wide range of learners. This has suggested to me the idea of beginning with a picture or a context (which can be everyday or purely mathematical) that learners might find enticing, along with an easy-to-understand question that they can quickly begin exploring (see, for example, Figure 4). This would seem to present much potential for learners to be drawn swiftly into the task, perhaps before they even realise that they are doing mathematics. Such a hook can capture learners’ involvement at the very beginning and channel their energies into rich mathematical activity.
Figure 4: Crazy Clocks
Beginning

Prompts
- Can you see what is wrong with the time on this clock?
- What happens if you rotate this clock?
- What time is it really? Can you be sure?
- Can you work out these times?



Source: www.mathematicalbeginnings.com
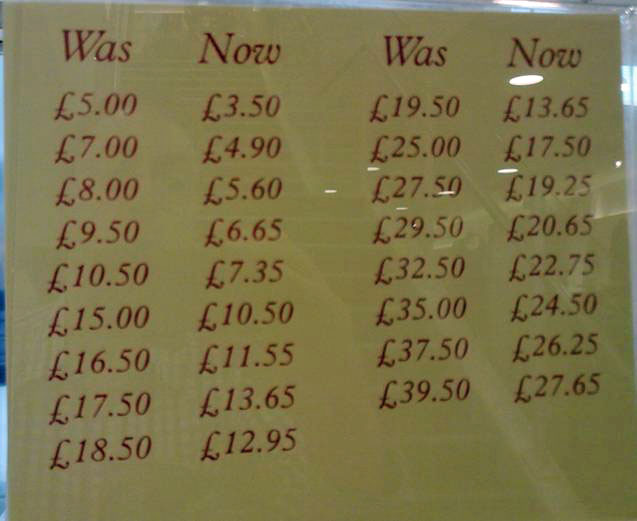
Many an excellent task is ruined by an unnecessarily long and off-putting introduction from the teacher, in which potential problems are highlighted and partially resolved. During such an exposition, learners’ initial enthusiasm evaporates as a potentially enticing problem is transformed into a tedious exercise, with all the sparkle squeezed out of it. Ollerton (2009) wisely advises that ‘It is worth contemplating how to get a class started on a task as quickly as possible, thus negating the possibility of turning the front of the classroom into a stage’. Ideally, the teacher should be able to speak for just a few minutes at the start of the lesson – or perhaps not at all – before asking ‘Does the task make sense?’, and this should lead to an affirmative answer from the majority of the learners. On the other hand, leaving aspects of the task vague or ambiguous can even be advantageous for the subsequent activity (Foster, 2011b). (For example, Figure 5.)
Figure 5: Crazy Clocks
Beginning
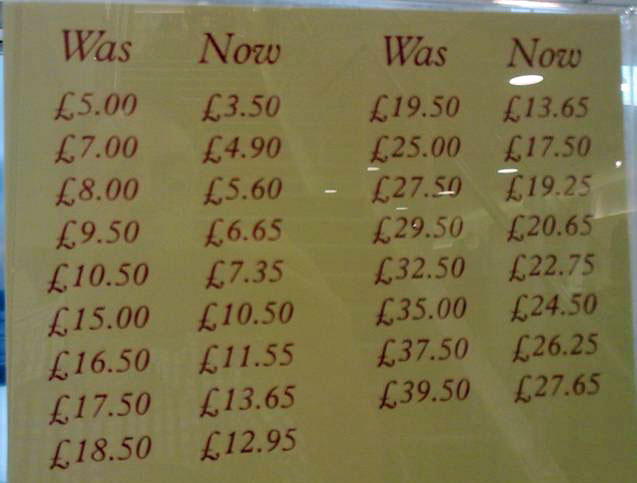
Prompts
- What has happened to these prices?
- Make a different ‘Was ... Now ...’ chart.
What patterns are there in its prices?
Source: www.mathematicalbeginnings.com
3.2 Accessible yet challenging
Figure 6: Highest Common Factor/Lowest Common Multiple

 Click here to see the full lesson plan.
Click here to see the full lesson plan.
Sometimes learners encounter the ideas of highest common factor (HCF) and lowest common multiple (LCM) as procedures to follow to obtain answers, without much sense of what these quantities represent or why the procedures work. This lesson builds up to having learners find numbers to fit a specified HCF and LCM, giving them an opportunity to explore what possibilities are allowed by these constraints. The trial and error involved also gives plenty of practice at the techniques.
The full lesson plan is available from www.teachsecondary.com.
The full lesson plan is available online from: www.teachsecondary.com/maths-and-science/view/lesson-plan-ks4-mathematics-highest-common-factor-lowest-common-multiple
While the first principle, enticing, relates to the initial setting up of the task, and to learners’ first impressions of it, the second principle of accessible yet challenging has more to do with what happens when learners begin to tackle the challenge and ‘get stuck into it’. An effective task must possess depth and challenge without appearing totally out of reach – a balance sometimes termed ‘low-entry–high-ceiling’ (Shade, 1991). An appropriate ramp to the task allows learners to begin immediately with something definite to do, such as exploring particular cases. Although the solution must not appear obvious to learners, the difficulty should not be experienced as intimidating if there are relatively easy calculations or procedures that learners can embark on straightaway, or drawings that they can make, that will help them to get ‘into’ the problem. (See Figure 6) Importantly, such processes are not an end in themselves but steps towards appreciating and tackling the larger task. Having such openings allows learners to gain some early achievement and success in obtaining initial results that will support further work. The overall task must be substantial enough to provide significant challenge. It must not appear trivial or be amenable to the straightforward application of a known technique. Throughout, it is important that there are multiple possible ways to proceed, so that learners do not feel that there is ‘one right pathway’, which others may be further along than they are currently.
3.3 Naturally extendable
Figure 7: Dots
Beginning

Prompts
- How many dots are there in this logo?
Can you work it out without counting them all? - Make some other ordered arrangements of dots.
Try to find ways of working out how many there are without counting them all.
The initial question ‘How many dots are there in this logo?’ may be answered simply by counting, but the subsequent prompts push for deeper thought and creativity.
Source: www.mathematicalbeginnings.com
This final principle relates to the mid-to-later stages of working on a mathematical task. The task must not lead to a dead end and resolve itself too neatly too soon. There must be further avenues to explore, both obvious ones and less obvious ones, which themselves provide appropriate access and challenge. This means that the task must possess sufficient depth and richness, so that there are unforced ways of extending it that come with the potential for significant challenge and learner creativity. This allows learners to make the task ‘their own’ and develop their mathematical independence in fruitful mathematical exploration. As learners become used to working in such ways, they frequently do not feel that they have really ‘begun’ until they have constructed an extension task for themselves, perhaps by asking ‘What if?’ questions, and embarked on it (Foster, 2011c). (For example, in Figure 7 the initial question ‘How many dots are there in this logo?’ may be answered simply by counting, but the subsequent prompts push for deeper thought and creativity.)
This third principle, perhaps more than the other two, cannot simply be ascribed to the task as designed, as though it were an intrinsic property of the materials. To a great extent, the degree to which a task is seen as extendible is ‘in the eye of the beholder’, and consequently dependent on the particular classroom climate that is operating. In a classroom in which learners habitually look for opportunities to be mathematical, even writing the date at the top of the page can manifest as a ‘naturally extendable’ task, in which questions about palindromic dates or other such features are spontaneously posed by learners. However, this third principle is important for the designer to take into account in ensuring that natural extensions to the task are considered at the design stage and made apparent so that it is easier for the teacher using the task to support the development of such a questioning classroom culture (Foster, 2011c).
This demanding set of constraints has led me to seek a design pattern, as this term is used in contexts such as architecture and software design. A design pattern refers to a widely-applicable solution to a commonly-occurring need in a particular context (Alexander et al., 1977). In order to design, on a regular basis, tasks that reliably meet these design principles, I have increasingly been led to a two-phase process which I call the Convergent-Divergent Model (CDM). I will discuss the features of this design pattern below.
4. The Convergent-Divergent Model
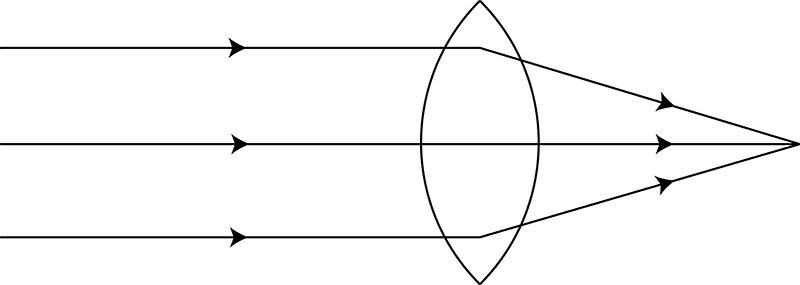
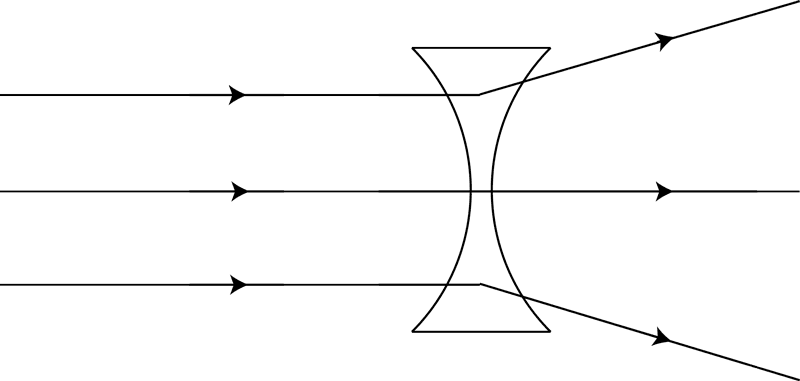
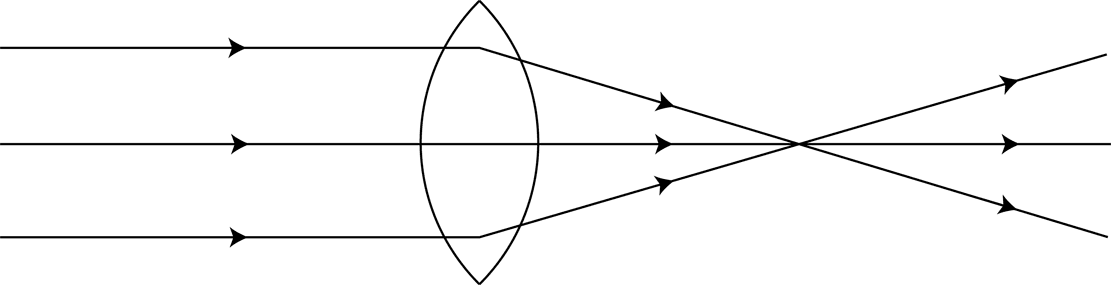
4The metaphor of a task as a lens has become important for me in thinking about principles for the design of mathematical tasks. A single task is never experienced in precisely the same way by different learners, or the same learner at different times, yet the varying interpretations are related, so I choose to represent the movement of different learners’ thinking by different rays of light being constrained in their directions by tasks, symbolised by lenses. I take a convergent task to be one which has a single, correct answer, which may be arrived at by a range of different methods. Thus, a convergent task, such as a focused problem-solving question, has a tendency to bring learners’ thinking towards a similar area (Figure 8), whereas a divergent task is more open-ended and provokes a more diverse range of outcomes (Figure 9). In each case, the diversity of learners’ initial thinking is represented by the different vertical starting positions of the different incoming rays; those that are more extreme are bent to a greater degree by the demands of the task than those nearer the centre, which deviate very little from their ‘natural’ path.
In the two-phase Convergent-Divergent Model (CDM) that I am explicating, an initial convergent task seeks to bring learners’ activity to one focus – the solution to the initial problem – but not as a final conclusion. It aims to harness the residual energy present at this point and use this to propel learners’ investigations forward into a divergent phase. The momentum carried by the light rays shown in Figure 10 compels them on, beyond the focal point, to subsequent divergence. In a similar way, in the CDM, the divergent phase is not ‘bolted on’, in the manner of many textbook extension tasks, which can have the appearance of time fillers for early finishers. By contrast, the divergent phase of the CDM is intended to take place in a natural and unforced manner as an outlet for the residual energy created by the accomplishment of the convergent task. As in Figure 10, because learners’ thinking arrives at the same point from a multitude of different directions, it is likely that when it proceeds it will do so with richly creative variety in many different directions.
Of course, learners’ thinking (rays of light) are not influenced only by the task (lens) but by the whole social environment of the classroom in which the lesson takes place. I think of this as the medium (e.g., air) through which the rays travel, and which may also bend them – or even block them completely – according to its varying properties. Subsumed within this contingency (Foster, 2015) are actions such as scaffolding, in which the teacher supports and manages the learners’ engagement with the task (Wood, Bruner & Ross, 1976). How this is effected is of course an extremely important aspect of what takes place.
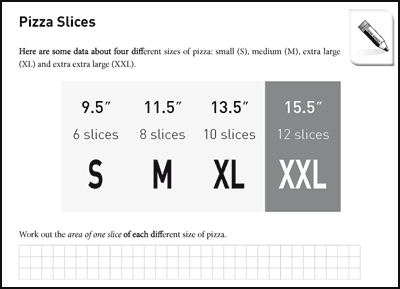
5. Pizza Slices: The lesson
5I will now attempt to exemplify the principles of the CDM through an analysis of the published lesson ‘Pizza slices’ (Foster, 2011a: 98–101) shown in Figure 3, explaining the design choices made and discussing the opportunities provided by the lesson.
The teacher notes suggest that the teacher begins the main phase of the lesson by asking:
Look at the data at the top about the four different sizes of pizza. What things do you notice?
This relatively open starting prompt was intended to place learners’ attention on the artefact. This image was redrawn by the publishers from the original (Figure 11) which I had used when I taught the lesson to my own classes. The original colour artefact had the advantage of being genuinely from the real world and recognisable by learners familiar with the pizza company in question. Displaying this via a data projector, without any task sheet headed ‘Pizza slices’, it was possible to begin in a more open-ended manner with:
What do you think this is?
Classroom discussion then flowed more conversationally about learners’ favourite brands and flavours of pizza, before I asked:
What mathematical questions could you ask about this?
In my own classroom, learners were accustomed to being asked this potentially divergent question in response to provocative starting images of various kinds (see www.mathematicalbeginnings.com; Foster, 2011c), so this was an easy way to begin. However, in the book, I chose to offer a more focused, convergent starting question, so followed up on ‘What things do you notice?’ with:
Suppose we buy one each of these four sizes of pizza. How many slices would that be altogether? … If I laid out the four pizzas here, all sliced into pieces, and said you could go first, and you wanted the biggest slice, which pizza would you take a slice from? Why?
I would not have phrased the question with so many caveats in my own classroom. With my own learners, I felt that it was more fun to allow comments such as ‘I don’t like pizza!’ or ‘That’s not fair!’ to emerge spontaneously rather than attempt to forestall them with conditions such as ‘you wanted the biggest slice’. However, when writing for colleagues I felt that it was wiser to try to prevent what might be seen as unnecessary problems that would detract from the mathematics being aimed for. With a very open starting point, there is the potential for learners to focus on other factors, such as price and value for money, which the teacher might be uncomfortable handling.
Within the CDM, this question represents a closed, convergent starting point which can, nevertheless, be responded to in several different ways, as I suggested in the book:
Some learners may think that they are all equal in size; others may think it would be better to take a slice of the biggest pizza, since it is the biggest; others may think that it would be better to take from the smallest pizza, since it is split into the fewest pieces; others may compromise and go for a medium or XL pizza. This should generate some disagreement, which could lead in to the rest of the work on the Task Sheet.
The first prompt on the task sheet is intended to scaffold learners (Wood, Bruner & Ross, 1976) towards a solution to this initial problem, the convergent part of the task:
Work out the area of one slice of each different size of pizza.
The subsequent prompts seek to offer further convergent lines of enquiry for learners who arrive at an answer to this first part:
Work out the length of crust of each different slice
…
What patterns do you find? Can you explain them?
Again, I would be unlikely to offer these prompts all at once in my own classroom. Learners would begin to work out areas and I might focus attention on lengths of crust later on, or this could emerge by asking learners to compare two pieces of pizza of the same area: ‘In what ways might they be different?’ But, when writing for colleagues, I wished to present all the relevant prompts on one piece of paper, for convenience. An alternative possibility would be to offer teachers a range of suggested questions and strategies from which they could select. In this way, the teacher notes themselves would become a more open text, susceptible to differing implementations. At the time, I considered that this would lead to notes that were too unwieldy and cumbersome to follow, but on reflection this is certainly something that I would consider attempting in future writing, particularly if using a hyperlinked, web-based format.
This initial convergent phase was intended to be enticing, by relating to learners’ interests in eating pizza, and the real-life question of getting the biggest slice. It was not immediately obvious which slice would be the largest, so there was a puzzling uncertainty about the problem. It sought to be accessible yet challenging, even to those who did not know the formula for the area of a circle, since there was the possibility of learners making accurate drawings or estimating using squared paper. The lesson starter offered in the teachers’ notes suggested asking learners to find the volume ‘of a pizza that is a cylinder of radius z and thickness a’, which is πz2a, which for humorous effect can be written as ‘pizza’. This has the serious purpose of reviewing the formula for the area of a circle prior to the main task and was intended to contribute to the accessibility of the initial convergent task via numerical calculation. This principle of reviewing relevant learning through a lesson starter is something that I have used frequently – especially as the lessons that I have written do not form a lesson-by-lesson curriculum but are intended to be used ‘as and when’, and therefore particular prior knowledge and skills of the learners cannot be assumed.
The divergent phase is introduced by the final prompt on the task sheet:
Suppose you want one slice of any pizza to be about the same size. Can you choose better values for the number of slices there should be in each size of pizza?
This was intended to be much more open-ended and challenging, though it can be pursued using whatever approaches learners have taken already on the convergent task. I offered almost exactly the same question in my own classroom. Although the task may lead to much practice of using the formula for the area of a circle, the intention is that learners might generalise, explore the interrelationship between the sequences of the diameters, the numbers of slices, the areas of one slice and perhaps the lengths of crust, encountering length and area scale factors and unexpected mathematical patterns.
 Click here for more…
Click here for more…
It is quite natural for learners to question the numbers of slices given in the advertisement, leading to an exploration of ‘What if they were different?’ I take this to be an instance of a naturally extendable task, forming the divergent phase in the CDM. The work that learners have done in the convergent phase is intended to be precisely the background necessary for the divergent phase. They have examined some special cases and are now invited to explore others and to generalise using the experience that they have just gained. In this way, the CDM seeks to realise the three principles outlined above in a design pattern that can be applied in numerous situations. For another example of a task employing the CDM, see Figure 12.
Figure 12: The Dishonest Teacher

This task concerns the test scores of children in five different classes and the effects on the mean scores of those classes when a child is transferred from one class to another. The context, in which a ‘dishonest teacher’ seeks to improve the mean scores of the five classes for which he has responsibility by shifting children from one class to another, is intended to be amusing without legitimating the deceptive use of statistics.
The first part of the task involves learners in calculating mean scores for the original five classes, and is a convergent, routine exercise:
Work out the mean mark for each class and write it in the bottom row of the table.
At this point in the task, learners are privy to the teacher’s private thoughts:
He thinks that some of the averages look a bit low. Then has an idea. ‘If I take pupil 5 out of class A and put him in class B, I wonder what would happen to the mean scores?’
Learners are asked to calculate the new mean scores for classes A and B, which is again a fairly procedural question, but requiring a little more thought (dividing by the new number of learners in each class). All learners should arrive at the same answers here, and this represents arrival at the ‘focal point’ of the CDM. Some surprise is anticipated, in that the pupil transfer raises the mean of both classes, and it is intended that this will generate some energy that will fuel the subsequent divergent phase.
For the divergent phase, the prompt is:
Which other pupils could be moved without reducing any of the means?
What do you think is the ‘best’ set of averages he can obtain by shifting pupils around? Why?
This represents a challenging and divergent episode, in which different learners will go in different directions. It builds on the conclusion reached in the convergent phase.
Source: Resources for Teaching Mathematics 11–14. (Foster, 2011a: 25)
Source: Resources for Teaching Mathematics 11–14. (Foster, 2011a: 25)
6. Conclusion
6I have attempted to show how the metaphor of a task as a lens has been important for me in developing the notion of the Convergent–Divergent Model (CDM). This approach to mathematical task design seeks to create tasks that are immediately enticing, where learners are engaged at once in productive mathematical work, with minimal explanation and introduction from the teacher. The CDM exploits accessible yet challenging tasks, which allow early successes that contribute to the solution of a more demanding problem. Learners are encouraged to follow different possible routes and make independent choices about their use of mathematics. The key feature of the CDM is its attempt to harness the energy created by the solution to the initial convergent problem to spur learners on to ask more open-ended questions and pursue challenging subsequent lines of enquiry. This naturally extendable aspect may lead to extremely varied learner responses, which I see as the most rewarding consequence of the task, and the episode that feels the most authentically mathematical. The intention is that if teachers enjoy seeing learners work more independently on their mathematics, they may decide to give them greater opportunities for such activity in other mathematics lessons, rather than a diet of purely convergent tasks. The CDM thus can be used to develop a convergent task into a more divergent one and contribute to a culture of asking rich exploratory questions about otherwise ostensibly closed mathematics (Foster, 2011c).
My assumption that convergent tasks are generally perceived as less threatening than divergent tasks might be challenged. The intention behind the CDM beginning with something convergent is to allow teachers and learners a safer beginning, during which energy is accumulated that can be put to use during a subsequent divergent phase. However, alternative models, such as beginning with a divergent prompt, which generates numerous outcomes, and then involving learners in selecting specific convergent lines of enquiry to pursue from this, would also be possible. There is undoubtedly a place for variety and the use of different design patterns. Beginning with divergence might be said to characterise exactly what took place at the start of my lesson, when I asked ‘What mathematical questions can you ask?’ Indeed, it might be felt that the process of design itself frequently takes a divergent-convergent form, as the designer ‘brainstorms’ numerous possibilities before narrowing them down to a particular set of ideas to implement.
In subsequent work I hope to explore the affordances of the CDM more widely across a range of areas of the mathematics curriculum and contrast learners’ experiences with those in other kinds of mathematical task.
References
iiAlexander, C., Ishikawa, S., Silverstein, M., Jacobson, M, Fiksdahl-King, I. and Angel, S. (1977). A Pattern Language: Towns, buildings, construction. New York: Oxford University Press.
Brown, A. L. and Campione, J. C. (1996). Psychological learning theory and the design of innovative learning environments: On procedures, principles, and systems. In L. Schauble & R. Glaser (Eds.), Contributions of instructional innovation to understanding learning (pp. 289–325). Mahwah, NJ: Lawrence Erlbaum Associates, Inc.
Foster, C. (2008a). Variety in Mathematics Lessons. Derby: Association of Teachers of Mathematics. An online resource is available at http://www.foster77.co.uk/variety/index.htm. Sample pages are available at http://www.foster77.co.uk/Variety%20sample%20pages.pdf.
Foster, C. (2010). Resources for Teaching Mathematics 14–16. London: Continuum. ISBN 9780826436030. Online resources are available at http://www.bloomsbury.com/cw/resources-for-teaching-mathematics-14-16/
Foster, C. (2011a). Resources for Teaching Mathematics 11–14. London: Continuum. ISBN 9781441142276. Online resources are available at http://www.bloomsbury.com/cw/resources-for-teaching-mathematics-11-14/.
Foster, C. (2011b). Productive ambiguity in the learning of mathematics. For the Learning of Mathematics, 31(2), 3–7. Available online at http://www.foster77.co.uk/Foster,%20For%20The%20Learning%20of%20Mathematics,%20Productive%20Ambiguity%20in%20the%20Learning%20of%20Mathematics.pdf.
Foster, C. (2013a). Mathematical Études: Embedding opportunities for developing procedural fluency within rich mathematical contexts. International Journal of Mathematical Education in Science and Technology, 44(5), 765–774. Available open access at http://www.tandfonline.com/doi/abs/10.1080/0020739X.2013.770089
Foster, C. (2015). Exploiting unexpected situations in the mathematics classroom. International Journal of Science and Mathematics Education, 13(5), 1065–1088. Available open access at http://link.springer.com/article/10.1007/s10763-014-9515-3
Swan, M. (2008). A Designer Speaks. Educational Designer, 1(1)."Introduction" Retrieved from http://www.educationaldesigner.org/ed/volume1/issue1/article3/#s_2.
Acknowledgements
I would like to thank Hugh Burkhardt and Malcolm Swan for extremely helpful comments on an earlier draft of this paper, as well as the editor and anonymous reviewers for their very useful suggestions. I would also like to thank Bloomsbury Publishing Plc for permission to reproduce the task sheets from Foster (2010) and Foster (2011a) and Papa John's (GB) Ltd for permission to include the image above from their pizza marketing.