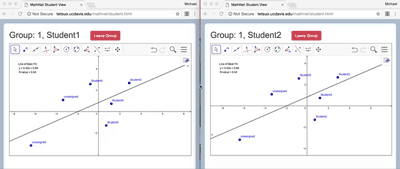
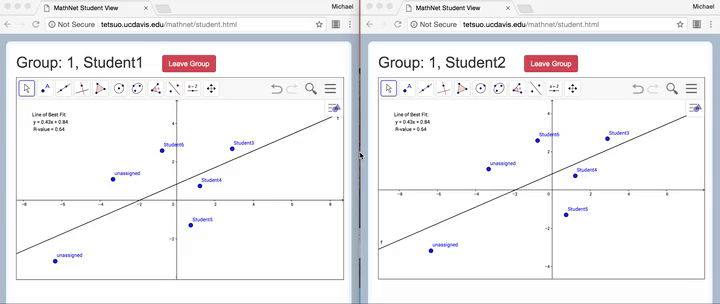
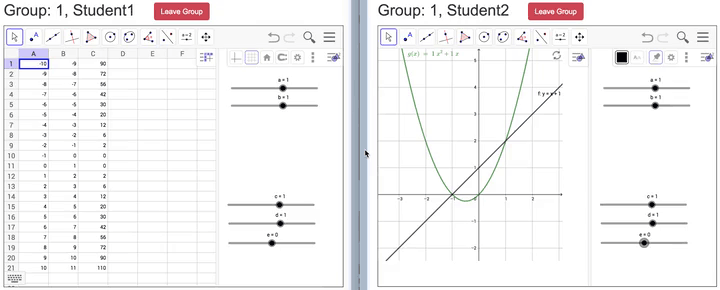
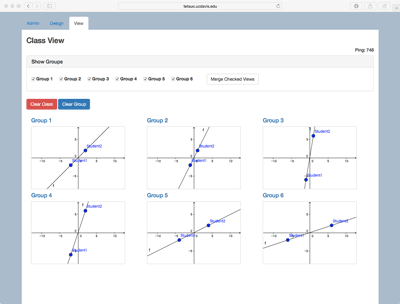
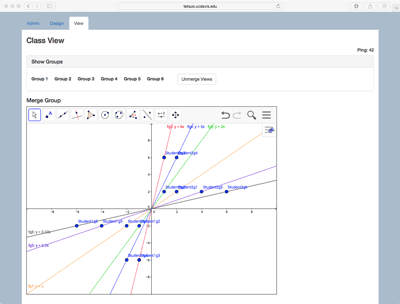
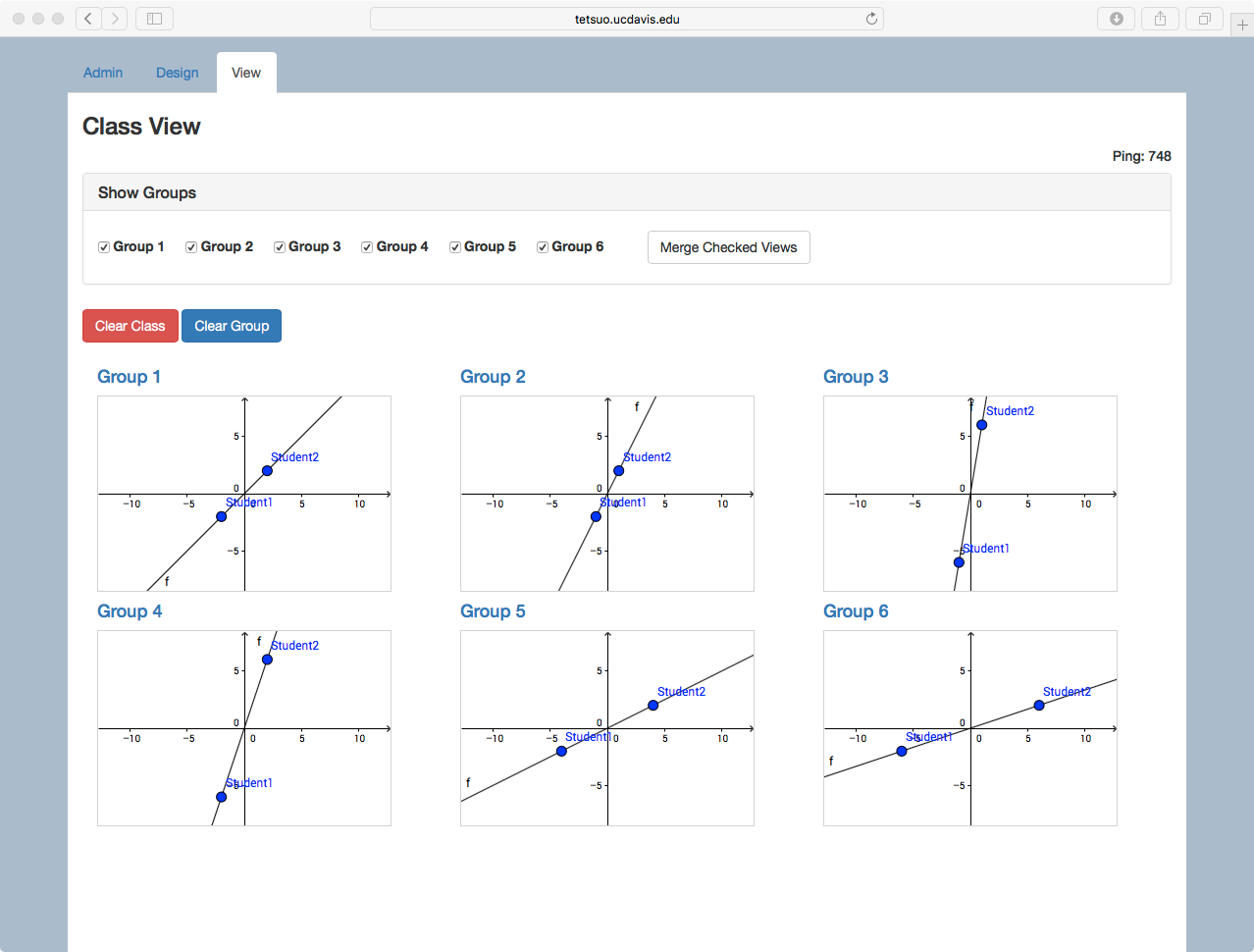
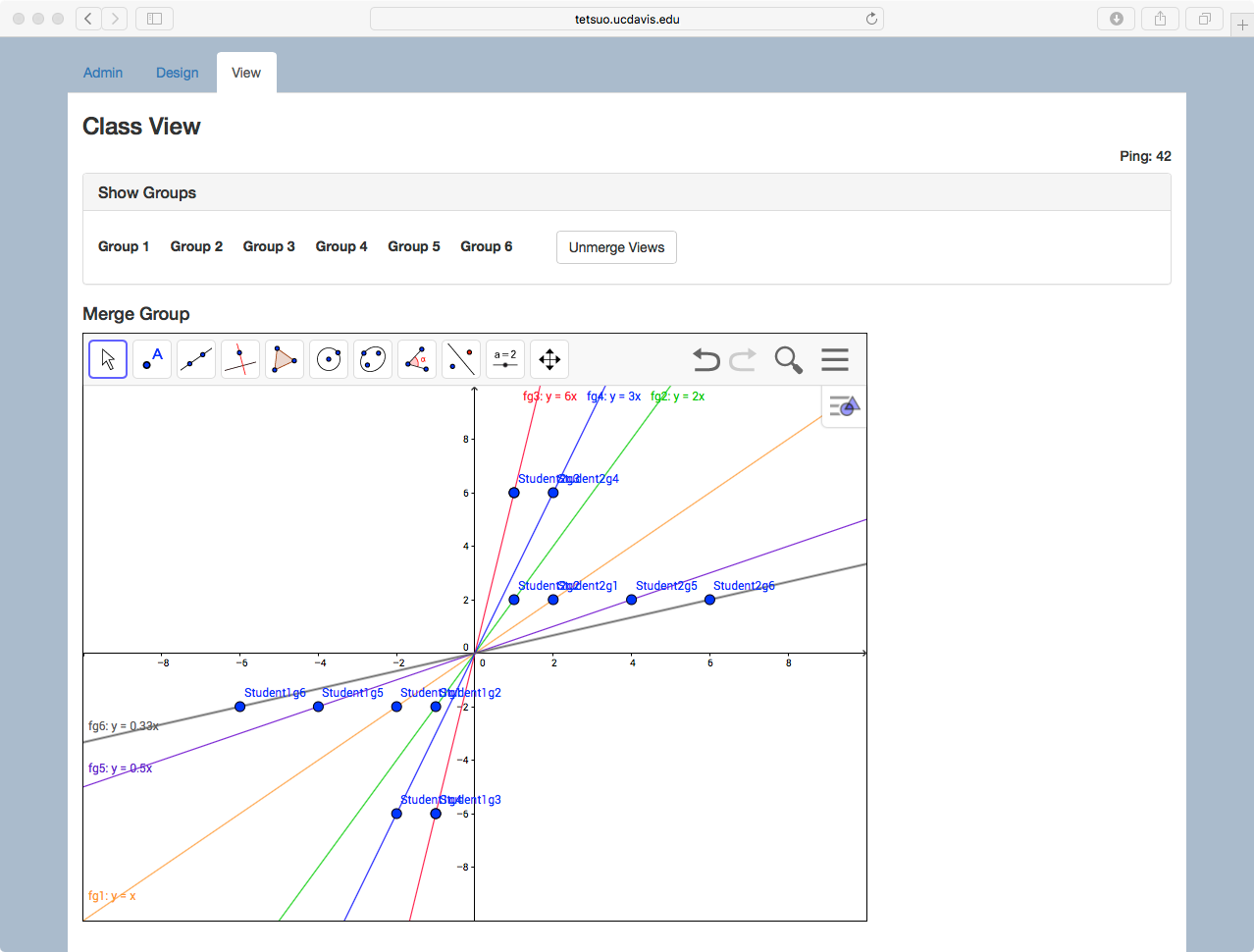
Though the Distributed-by-Design approach we have described here emphasizes small-group collaboration, many activities can be naturally extended to the level of the whole class. Figure 4 illustrates a simple extension of the linear Graphing in Groups case from the small group to whole class level. The MathNet teacher interface includes a viewing panel where graphical windows of all student groups are simultaneously displayed (see Figure 4a). This view enables the teacher to monitor the progress of each group, and it can also be projected to the front of the room to support class discussion, or interaction between groups. Moreover, the mathematical objects created and controlled by each group can be merged into a single whole-class aggregate window in order to highlight patterns or relationships among different groups’ constructions (see Figure 4b). In this example, student pairs are asked to form lines that have different slopes but pass through the origin. Then when the views are merged, the class can discuss similarities and differences among the resulting lines. Further, the merged view can prompt portions of the conceptual territory that have not yet been explored (“Can anyone create a line that crosses from the top-left to the bottom-right?” or “Can anyone make a line that hugs very close to the y-axis?”). Thus even as small group-level interactions within each student pair are structured around the relationship between two points and a line, class-level interactions across pairs can be likewise structured by the mathematical relationships among members in a family of functions and can help to map a mathematical space (cf., Stroup, Ares, Hurford & Lesh, 2007; White, 2018).

A Distributed-by-Design Approach to Supporting Collaborative Learning with Dynamic Mathematics Software
Tobin White1, Corey Brady2, WenYen Huang3 & Michael Stevens1
1University of California, Davis, 2Vanderbilt University, 3SUNY-New Paltz
Abstract
iFostering productive groupwork is a goal for many educators, but it can be difficult to implement effectively in mathematics classrooms. We have developed an approach, and a corresponding set of new tools, intended to support student participation in mathematically rich collaborative learning activities. This paper provides an overview of this ‘Distributed by Design’ approach. We elaborate key principles by illustrating three variations, in which we alternately distribute distinct but interdependent mathematical objects, views, or tools to each student in a cooperative group, and ask participants to coordinate those elements in completing a shared task. This approach is implemented with our MathNet software.
Introduction
iiIn our ‘Collaborative Learning In Classroom networKs’ (CLICK) Lab at UC Davis, we design software applications and learning activities aimed at creating new ways for small groups of students to work together to solve problems and explore concepts. This paper presents an overview of our design rationale and approach. We describe an application and how it might be used by students in several examples of mathematics learning activities illustrating our approach.
Cooperative and collaborative learning approaches have long been heralded as a powerful resource for educators to use in supporting student achievement (Johnson & Johnson, 2009), fostering dialogic interaction and shared meaning-making (Stahl, 2006), and encouraging equitable participation (Cohen, 1994). At the same time, productive groupwork can be notoriously difficult to successfully implement and sustain, because some peer discussions may quickly veer off-topic, or groups may divide labor in ways that minimize opportunities for substantive interaction and shared-meaning-making, or some participants’ contributions might be overlooked or undervalued, or some students may simply dominate discussions or complete the task in isolation while others may opt out of participating or feel excluded (Barron, 2003; Cohen, 1994; Salomon & Globerson, 1989).
Our design approach seeks to provide students with tools and tasks that maximize the potential benefits of groupwork while minimizing occurrence of the accompanying difficulties. We use group structures and interactions to construct learning environments where innovative forms of learning and participation can unfold, while minimizing the probability and risk of negative group dynamics. Our principal strategy for accomplishing that balance is an approach we call Distributing by Design (White & Pea, 2011). This model draws its name and its inspiration from theoretical and empirical accounts of distributed cognition—in which the unit of analysis for conceptualizing and studying cognitive activity is taken to be broader than the internal mental activity of a single agent, encompassing a system of people and tools collectively engaged in the accomplishment of a particular task (Pea, 1993). A seminal account of distributed cognition describes the joint efforts of several participants coordinating a complex array of instruments and representations in order to steer a large naval vessel along a coastline (Hutchins, 1995). This navigation team relies on the performance of computational work by, and communications among, several human actors and an array of material artifacts to complete a task no single participant could accomplish alone. CLICK designs emulate this example of what Hutchins called “cognition in the wild” by
- using networks of personal digital devices to distribute multiple related problem elements, representations, and resources among multiple students, and
- posing problem-solving tasks that require coordination across those elements and resources for their successful completion.
In order to ensure that these distributed tasks not only encourage all group members to contribute but also support students’ developing understanding of important mathematical ideas, we also draw on a principle of “generative design” (Stroup, Ares & Hurford, 2005). Through generative design we can establish relations between mathematical structure and the social structure of a classroom group to support learning activity design.
Bringing these frameworks for distributed and generative design together in the context of mathematics learning means mapping the collaborative relationships among participants to the mathematical relationship(s) that the learning activity seeks to help students understand. In particular, we begin by identifying important disciplinary concepts that center on relationships among an appropriate number of mathematical objects or conceptual elements. Ideally this will be two to four for small group work, but potentially many more for larger group and whole-class work. We then develop software tools that distribute those objects or elements to the devices of a corresponding number of students, and synchronize the states of those objects on each device to maintain the target mathematical relationship. Finally, students in an instructional setting are presented with a series of tasks that require them to modify the element(s) they control in order to produce a particular configuration or instance of the target relationship.
A simple but illustrative example of the small-group context comes from work on linear functions. Linear functions are simple and uniform and thus the entire relation can be determined by the function value at any two inputs. That is, two input-output pairs, such as two graphical points, uniquely determine a line. In an activity called Graphing in Groups (White, Wallace & Lai, 2012), we plot those two points onto a Cartesian graphing window displayed on the respective devices of two students, each of whom can move only his or her assigned point. Each time one of the participants selects new coordinates, the application re-draws the line between their points accordingly, so the linear function is jointly determined by contributions of the two students. Graphing in Groups tasks then ask students to position their respective points so as to produce a line with particular characteristics. For example, they might be asked to form a line featuring a slope of 3/2, or passing through a specified point, or perpendicular to the line of another group.
The Graphing in Groups activity shares some common features with an early exemplar of participatory simulations for mathematics classrooms called the Function Activity (Wilensky & Stroup, 1999). In that design, each student in a whole classroom group used a laptop computer or graphing calculator to plot points in a shared graphing window that conformed to a rule announced by the teacher (e.g., “Make your y three times your x” or “Make your y three more than twice your x”). The patterns that emerge from these aggregates of student-generated points provide rich opportunities for the class to discover, discuss and explore linear functions (Brady, White, Davis & Hegedus, 2013).
These two related designs connect different aspects of the same mathematical structure to different scales of classroom social structure to support correspondingly different learning activities. In the Function Activity, the focus is on how a whole classroom group of students contribute many points that collectively produce a linear graph. In Graphing in Groups, student pairs dynamically explore lines uniquely determined by their two points. These small groups usually find that in order to complete these tasks they need to communicate about strategies and coordinate their actions. In the process of formulating those strategies and carrying out those actions they often have occasion to discover and reflect on salient aspects of linear functions and their graphs showcased by this setting. For instance, in working on the challenge of creating a line of a given slope, pairs of learners engage with one of several strategies for monitoring the slope of a line from the coordinates of two movable points. These include fixing one point and moving the other, moving one point to a particularly “easy” starting point (the origin or y-intercept, for example), or moving in coordinated ways shifting only x or y at a given time. These different pair-level strategies can emerge in later whole-class discussion and provide resources for understanding (for example, understanding the different forms of the equation for a line).
MathNet
1For many years, our efforts to develop activities like this one relied on customized software applications, each of which implemented a single instance of this approach. While the Graphing in Groups design centered on a student app that enabled moving Cartesian points and viewing linear function graphs, other activities required applications equipped with different representational tools. Recently, we have begun developing a new application, called MathNet, as a means of generalizing the Distributed-by-Design approach to a much wider range of secondary mathematics curricular topics and learning activities, all of which can be customized by users through a single web-based platform. Below, we describe the MathNet platform (CLICK Lab, undated) and elaborate the ways it enables and extends a Distributed-by-Design approach. The software can be run in standard internet browsers for use by teachers and students.
Distributing by Design with MathNet
iiiThe MathNet platform is intended to support a wide variety of activities that follow the Distributed-by-Design approach. To explore a wide initial design space, we first integrated a prominent open-source, web-based dynamic mathematics software application, GeoGebra (GeoGebra Enterprise, 2018) with a flexible, group-aware communication system in order to support collaborative learning activities in secondary mathematics classrooms. In doing so, we built on work conducted by the Virtual Math Teams (VMT) project, which pioneered efforts to create and investigate a multiuser dynamic geometry platform to support mathematics learning (Stahl, 2009; 2015). However, whereas the VMT software was designed to support collaboration among groups of learners in an online format, the MathNet platform is designed for integration into face-to-face classroom settings. MathNet includes browser-based interfaces for both students and teachers. Each student user logs into a virtual classroom created by the teacher, and then joins a group. Students in a group enter a multiuser version of GeoGebra; any group member can construct and manipulate mathematical objects that are then visible to all group members. The MathNet teacher interface provides basic functionality for creating and maintaining a class, and for setting up conditions for group collaboration in a particular activity. These include three core variations on the Distributed-by-Design approach: distributing objects, views, and tools. These three collaboration scenarios are elaborated below.
Distributing Objects
1The Graphing in Groups example above illustrates how the task of finding a linear function with nominated properties can be distributed among a system of participants and tools by establishing a mapping between a set of related mathematical objects and a set of collaborating students. In this design, each student of a collaborating pair controls one of the points that define the line. MathNet enables the expansion of this approach to include other mathematical objects and relationships. A foundational element of the MathNet design is that each free or independent mathematical object (in the Graphing in Groups case, a Cartesian point) is associated with, and therefore can only be edited by, one designated student. For all other members of the multiuser GeoGebra group that object is ‘read-only’—it can be viewed, but not manipulated. In contrast, dependent objects (such as a line, line segment, or polygon connecting points created by one or more users) can be added by any user, and they vary dynamically with actions on any underlying independent objects. Consequently, students in the same small group can jointly explore properties of dependent objects such as functions and their graphs, or geometric constructions composed of multiple dependent objects, by manipulating their respective independent objects.
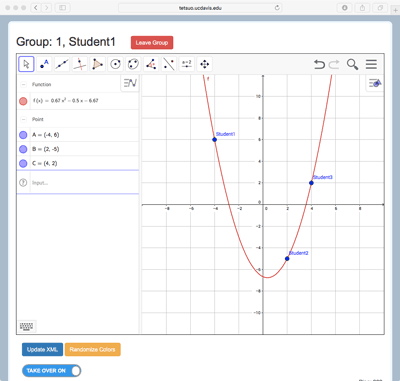
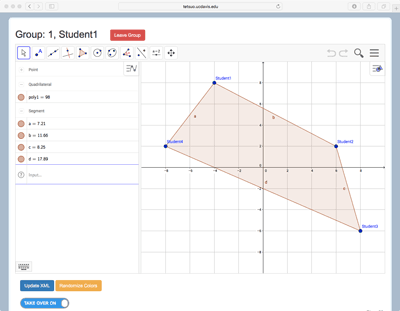
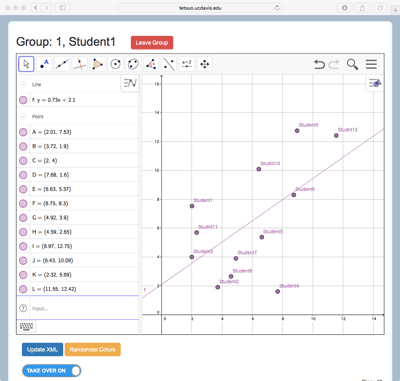
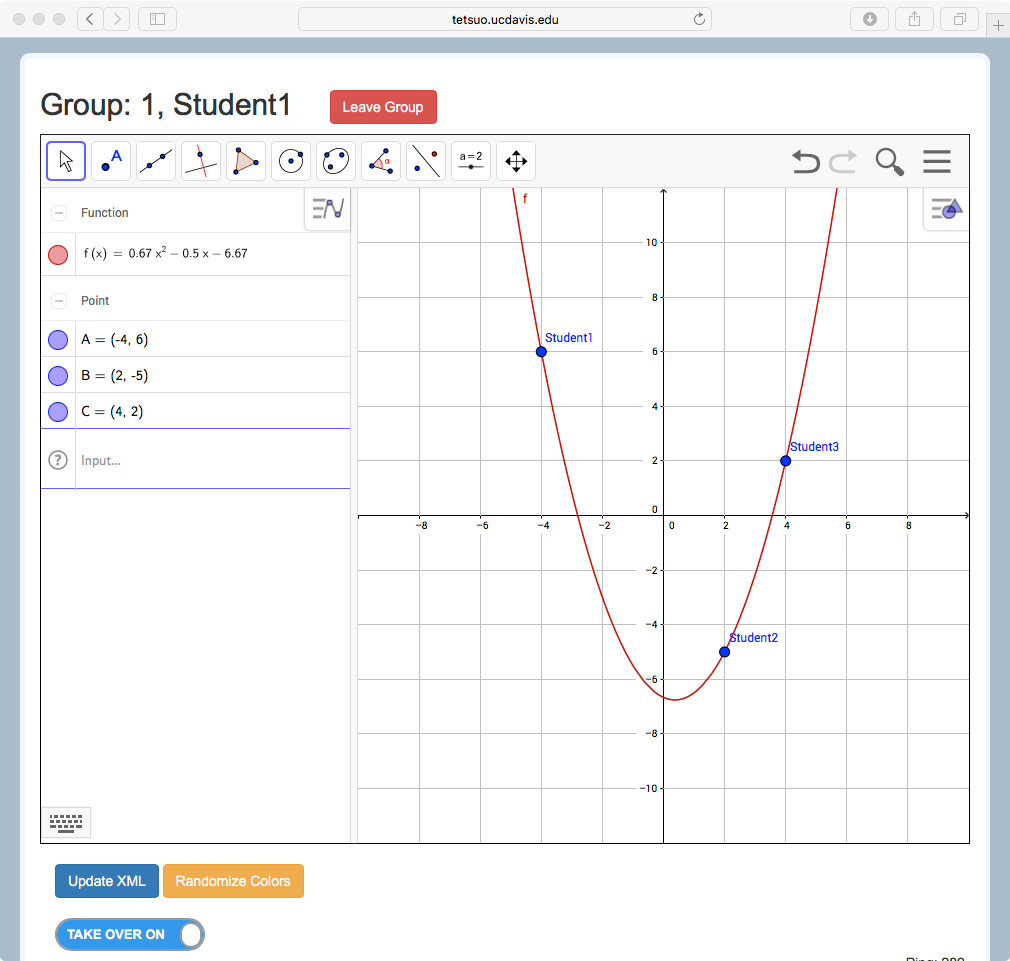
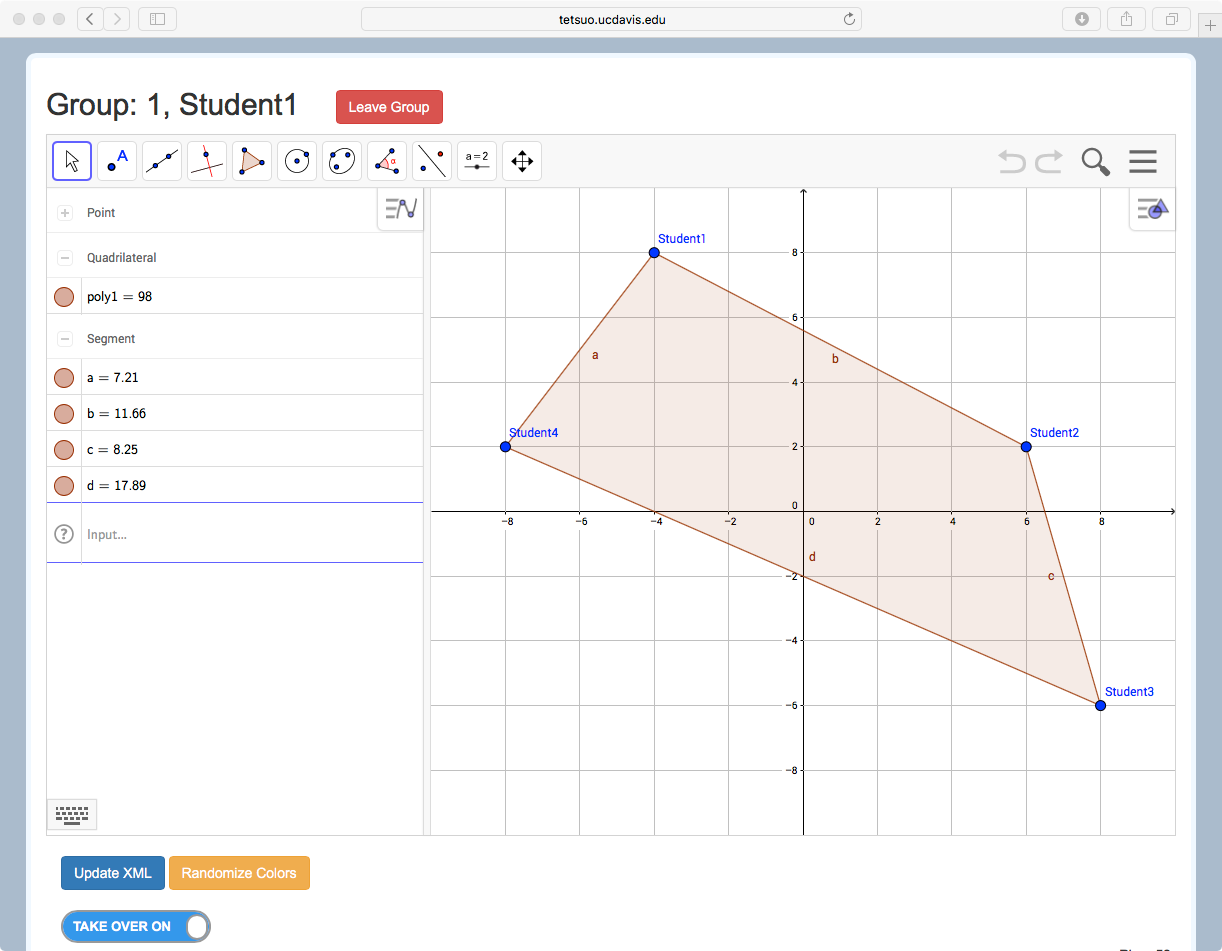
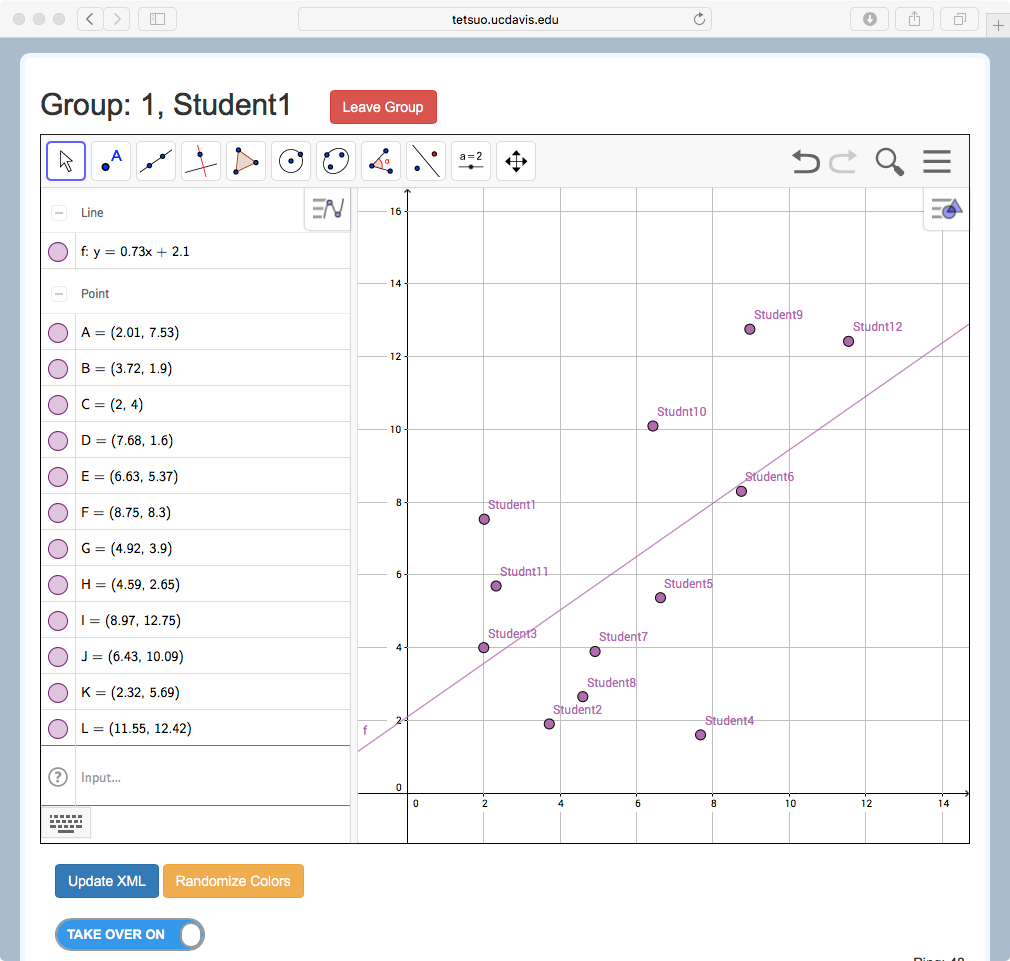
MathNet extends the Graphing in Groups activity described above from the case of two students and linear functions to any number of student participants, and to a much wider array of independent and dependent objects. In general, each student controls aspects of one or more independent objects. Examples include the coordinates of a Cartesian point, the value of a parameter, the contents of a spreadsheet cell or column, or the measure of an angle. The students also create, or the teacher introduces, other mathematical objects that have dependencies on multiple students’ independent objects. For example, three students’ points might be the hotspots that enable manipulation of a quadratic function (Figure 1a), or four students’ points may define a quadrilateral (Figure 1b), or many students’ points be the data for a line of best fit (Figure 1c). Students might likewise explore properties and create configurations of other dependent objects by adjusting sliders, inputting numerical values, or taking other actions on independent objects. In this way, fundamental mathematical relationships and concepts embodied in these dependency relationships are effectively layered onto, and thus can be exposed by, actions by and interactions among participants in the group. Example 1: Distributed Objects (see Figure 1d) is a short video that demonstrates how the activity in Figure 1c works.
Collaborative learning activities centered on distributed objects invite students to explore the relationships between their own (independent) mathematical objects and the group’s (dependent) collective object(s). When asked to construct a linear function with a particular slope, or a quadrilateral with certain characteristics (e.g., a parallelogram), students often begin by moving their points experimentally, using trial-and-error strategies or visually approximating the target object. Over the course of sequenced tasks, and through dialogue and discussion, groups gradually discover more systematic solution strategies and resources for completing these tasks, such as stepping their points through the rise-and-run of a slope triangle, or attending to side lengths and angle measures (Lai & White, 2012; White, Wallace & Lai, 2012).
Distributed-objects activities also challenge students to learn how to coordinate their actions with one another. Initially, students often try to complete tasks in isolation, only to discover that the objects they seek to create depend on their peers’ actions as well as their own. For example, we have documented the efforts of one student who sought to construct a line with a slope of 3/1 by moving her own point up three units and over one. Only after unsuccessfully trying this approach did she realize that this slope depended not on the movement of her individual point but the relation between her point and her partner’s. She then began to work with her partner in this and successive activities to synchronize their respective point movements to form lines with specified slopes (White, Wallace & Lai, 2012).
Distributing Views
2Like independent objects, different representations or views of the same mathematical object(s) can also be assigned to different members of a group to enable Distributed-by-Design scenarios. A foundational idea behind the use of technologies such as graphing utilities in mathematics education is that these tools dynamically link multiple representations of an underlying object, such as a function, so that students might have opportunities to observe and reflect on relations between or invariances across those representations (Kaput, 1989; Moschkovich, Schoenfeld & Arcavi, 1993). At the same time, in single-user learning environments, it is often a challenge to gauge to what degree the learner is making connections across representations, or even registering and making sense of connections that a software environment is making for them (cf., Kaput & West, 1994). Layering interactions and connections across multiple mathematical representations on top of group structures provides a resource for addressing this persistent issue in learning and design (White, 2006). As students in a small group express ideas and intentions verbally, they surface ’bugs’ in their thinking; and within activities designed to promote such exchanges, articulating directions for each other across representational boundaries supports learners in thinking about links between representations more explicitly and thoroughly.
GeoGebra includes several integrated representational perspectives on the same underlying document: an algebra view, a graphical view, a spreadsheet, a computer algebra system (CAS) view, a 3D graphing view, and others. MathNet enables a teacher to select the views available to each user in a class, and to assign different views to different students in the same group. For example, multiple users can simultaneously observe the effects of varying parameters on a function displayed in windows with different dimensions for each user. Or, one student might have access only to the Algebra tab, another the Graph, another the Spreadsheet—occasioning opportunities for participants to investigate, discuss, and compare affordances of different representations of the same function across their respective views (White & Pea, 2011).
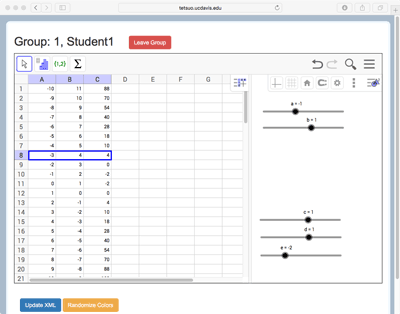
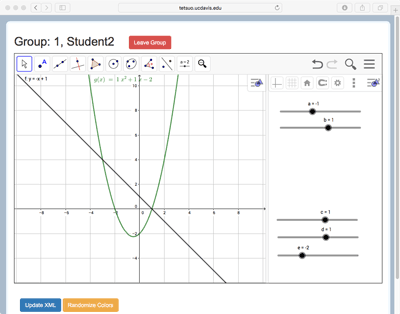
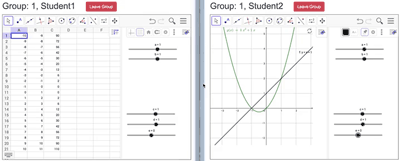
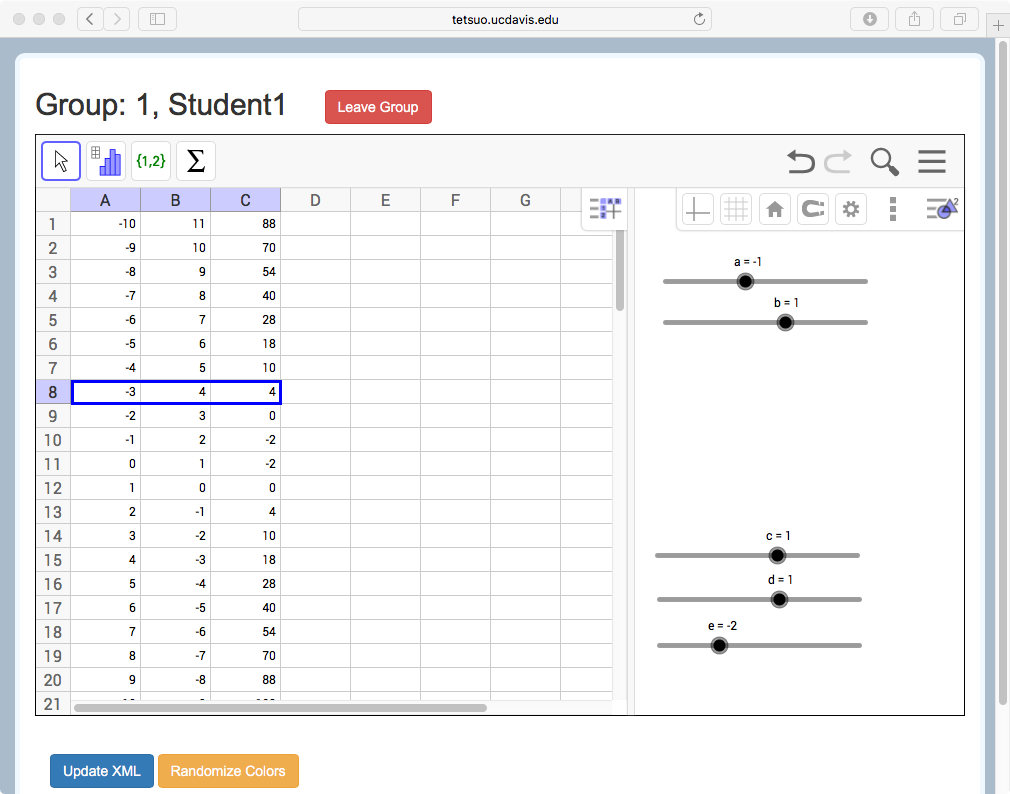
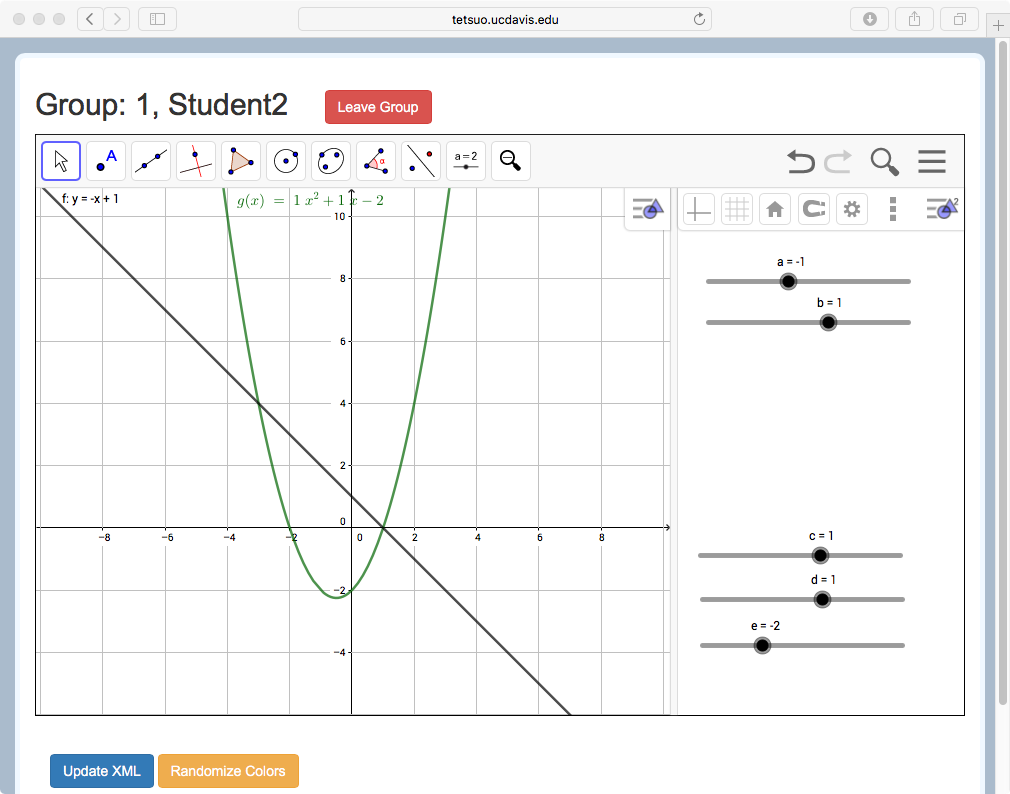
As a simple illustration, consider the situation depicted in Figure 2a and Figure 2b and illustrated in the short video in Figure 2c. In this instance, each student sees the Algebra view, listing two functions ( and ) with five slider-controlled parameters (a, b, c, d, and e). Student 1 also sees the Spreadsheet view, currently displaying a table of values for f(x) (in Column B) and g(x) (in Column C) corresponding to the input values in Column A (Figure 2a). Student 2 see the graphs of the two functions but not the spreadsheet (Figure 2b). The two functions are dynamically linked between these displays, so that as any of the sliders are adjusted, students see the changes to the sliders and their respective function displays. To further scaffold collaboration, a distributed-representations activity can be combined with distributed objects; in the example of Figure 2 Student 1 has control of sliders a and b while Student 2 can adjust sliders c, d, and e. The group can explore variations of these functions and relationships between them, compare the tabular and graphical views, and complete a wide variety of tasks. For instance, groups could be challenged to create linear and quadratic graphs that have an intersection point as close to (1, 1) as possible but not equal to it. This challenge makes differential use of the graphical and tabular representations, as well as opening up debate about meanings and strategies for approximation and different possible meanings of ’close.’
An elaborated variation on this distributed representations task engaged students in cryptanalysis challenges. Groups received a string of numbers representing an encrypted message and were asked to combine multiple graphical, algebraic and tabular views to seek polynomial functions that could have been used to encode a message by generating those numbers from the ordinal values of the letters in the alphabet (White, 2009). We have found that this distribution of different dynamically linked representational resources to different members of a small group can support novel ways for students to participate in collaborative problem solving (White, 2006). Of course, novel interactions are valuable only when they highlight mathematical relations in new and illuminating ways. Activity designs with MathNet unfold through resonances between the structure of tasks, the structure of mathematical objects or constructs; and the structures of groups. The most successful activities provide a coordinated group the opportunity to grapple with important mathematical structures as a group, working simultaneously in an interpersonal discursive space and a collaborative interactional space mediated by customized MathNet interfaces. Moreover, the challenge of coordinating multiple representations across multiple devices occasioned opportunities for students to devise novel ways of interpreting, applying, and combining representational tools as they developed increasingly sophisticated code-breaking strategies (White, 2008; White & Pea, 2011).
Distributing Tools
3A third variation on the Distributed-by-Design approach involves equipping each student in a small group with different tools relevant to completing a problem-solving task. Each GeoGebra view features an array of tools for creating or acting on mathematical objects. These include sets of tools related to points, lines, circles, polygons, transformations, factoring, regression analysis, and so on. MathNet enables teachers to customize the toolbar menu available to each member of a group, so that each user sees and is able to select different tools. Groups can then be asked to undertake construction activities for which no single student has access to all the tools necessary to complete the task, so that students must work together to accomplish a shared objective (Johnson, Johnson & Stanne, 1989). Like the use of role assignments common in classroom group work, distributing different tools to different group members provides distinctive ways for each student to contribute to collaborative activity, encouraging participation from all students (Cohen, 1994).
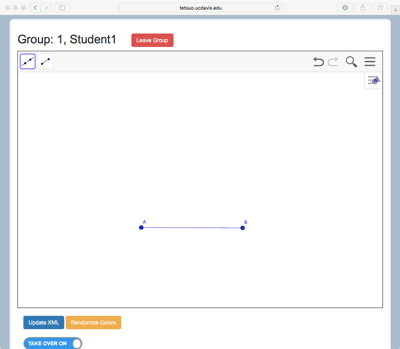
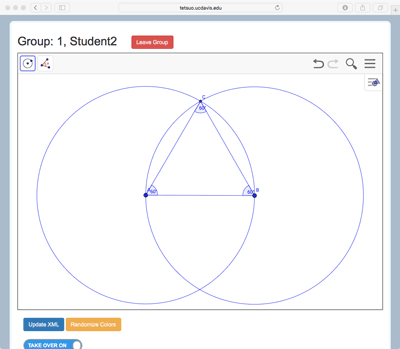
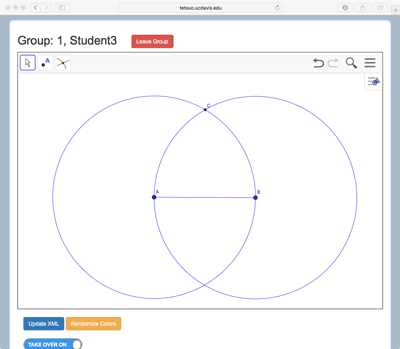
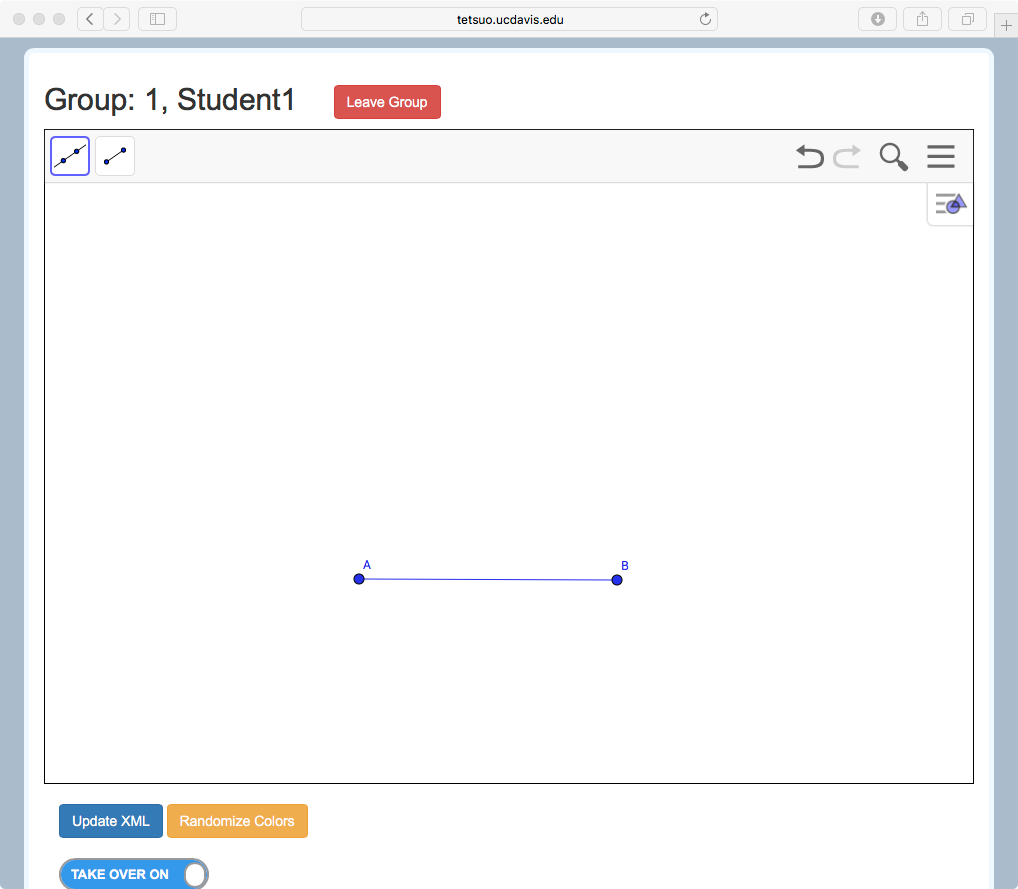
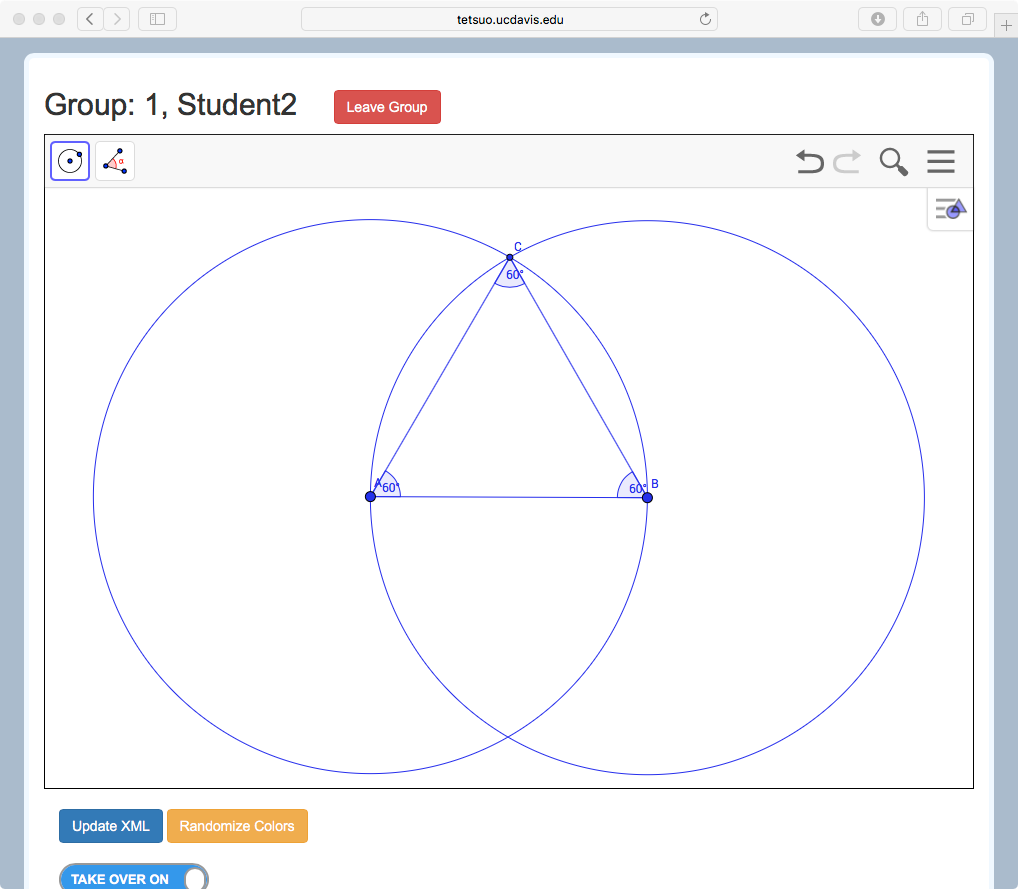
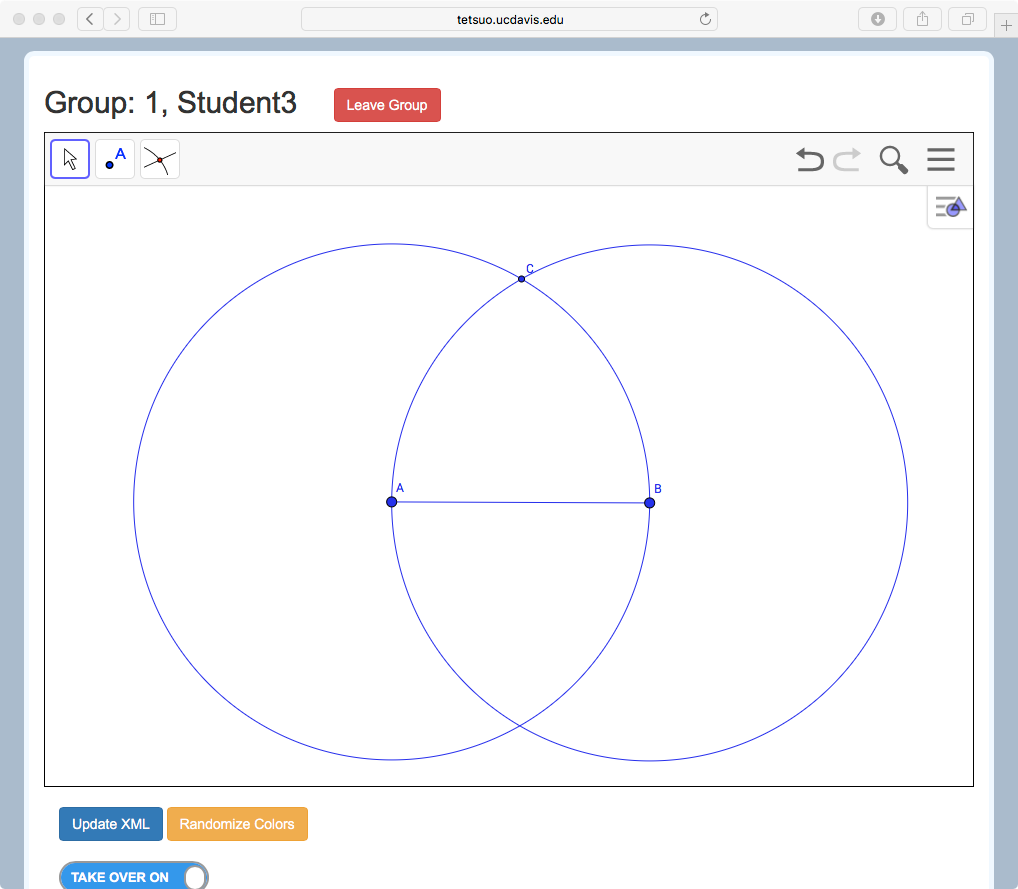
The example of Figure 3 (see short video in Figure 3d) shows the case of three students who have different tools. Student 1 has the line and line segment tools, Student 2 has circle and angle measure tools, and Student 3 has point creation and selection (move) tools. A variety of classic geometric constructions can be made by using these tools together, such as the equilateral triangle highlighted in the first Proposition of Euclid’s Elements. Stahl (2015) has shown how replicating this construction can introduce students to dependency relationships and dragging practices in a dynamic geometry environment. Figure 3d shows how to construct an equilateral triangle. Student 1 might begin by creating a line segment connecting Points A and B (Figure 3a). Student 2 could then create two circles, one centered at A and one at B, both with radius AB. Student 3 might next create Point C at an intersection between these two circles Figure 3c). Student 1 could then add Segments BC and CA to form a triangle, and Student 2 could measure the three interior angles (Figure 3b). Finally, Student 3 could use the move tool to drag Points A and B, so that the group would observe the invariance of the angle measures and conclude the triangle is always equilateral.
Activities in transformational geometry and the generation of tessellating patterns have also used tool distribution to support student participation in collaborative mathematics learning activities. To construct a tessellation of the plane with a generic quadrilateral, for example, groups would need to coordinate applications of translations and rotations. In some cases, reflections can be used, and in many cases, more than one procedure for combining these transformations can yield a successful tessellation.
Limitations and Challenges
ivDistributing objects, representations, and tools in the ways described above each create conditions that encourage the active participation of all members in a student group by allocating distinctive resources that are each essential to the completion of an assigned task — a condition of resource interdependence that is an important characteristic of cooperative learning activity (Johnson & Johnson, 1987). Distributing interdependent objects among multiple students does not, of course, guarantee that those learners will cooperate in the ways intended in these designs. Sometimes, for example, one student takes control of another’s device in order to access their object, view or tool. Or, in some instances, a student may feel that his or her assigned role and resources are less crucial to successful completion of the task than those of other group members. Or, a student with responsibility for a crucial tool or representation may be reluctant to participate in the activity, impeding the group’s progress. Such challenges can be found in any cooperative learning environment, and no design can promise to eliminate them.
On the other hand, even when distributions of resources do not yield the intended interactions among peers, they may nonetheless support conditions for productive student collaboration. For example, consider the case of three students using distributed tools to construct an equilateral triangle, as described above. In our design-based research investigations with the MathNet system, we have observed a group working on this task in this configuration and discovered that the student in Role #3, with point and selection tools, complained that he had limited opportunity to participate because his tools did not play as substantial a role in the construction activity as those of his groupmates. This situation was exacerbated when the student in Role #2 discovered she could use her line segment tool to create the endpoints of a line segment, as well as to connect existing points, so that Student 3’s participation was not even necessary to create the triangle base AB shown in Figure 3a. Over the course of the session, however, as the group moved on to the more challenging task of constructing another equilateral triangle inscribed in a circle, Student 3 played a central role in proposing, discussing and debating possible solution strategies, and eventually even discovered a novel way of using his selection tool to help the group evaluate elements of their construction.
So, while distributing by design did not unfold as scripted in this episode, it nonetheless shaped an environment in which the group maintained shared focus on and sustained dialogue about a set of mathematics tasks for a full hour. Indeed, we see distributed designs not as scripts specifying particular interactions among students and mathematical objects, but rather as conditions that contribute to the potential for productive collaborative learning sessions. They certainly do not override—but rather complement and should be used in combination with—other conditions for successful cooperative learning, such as effective teacher facilitation or the establishment of appropriate classroom norms for groupwork (Cohen, 1994). And distributions of these resources should be treated flexibly, through rotation of tools or views among different group members over successive activities and variation of the elements in assigned toolsets as appropriate in successive steps or iterations of a task.
Structuring and Sequencing Learning Activities
vCollectively, these flexible means of distributing objects, views and tools among participants enable a virtually endless variety of possible scenarios for structuring group-centered mathematics tasks and investigations. Though the interactions among problem elements are structured, tasks can have a single solution, or can be open-ended. For example, in a scenario where three students move three points that jointly determine a quadratic function, they might be asked to construct the graph of a specific parabola, such as y = 3x2 – 7. Or, they might be asked to explore and discuss how each of the parameters in a standard-form quadratic (ax2 + bx + c) vary as they move their respective points. Or, they might be invited to graph a series of parabolas that form an interesting pattern. Broadly, Distributed-by-Design tasks might focus on exploration of an existing set of mathematical objects, or construction of new ones, or analysis of those different objects across multiple views, or explanation of a mathematical relationship or phenomenon, or creative expression using shared mathematical objects and distributed resources.
Different approaches to distributing lend themselves to different types of tasks. Distributing objects that are sub-elements of an existing geometric construction, for example, is well-suited to having students participate in an exploration task, whereas having students create that construction themselves may be better aligned with a distribution of tools. Indeed, combining tasks that feature different distribution strategies can be an effective way to sequence collaborative learning activities over the course of one or more classroom sessions.
From Small Group to Whole Class
1In developing MathNet further, a number of our design questions focus on the teacher’s use of class-level views. For example, what tools support the teacher’s role in facilitating movement between small-group and whole class activities and discussions? What kinds of questions and visualizations can support classroom groups in opening up and exploring mathematical structures and spaces at multiple levels? And, what kinds of planning and preparation position the teacher well to identify and make use of the opportunities for facilitation that emerge as learners engage in MathNet-supported collaboration?
Extending beyond Mathematics
2While MathNet’s focus on secondary mathematics and GeoGebra has been an important way to bound our current research and design efforts, Distributed-by-Design approaches hold potential for group-centered learning in other domains and disciplines. We have explored how different representational infrastructures can be combined to enable comparable activities in physics and other STEM fields (Hardy & White, 2016). Furthermore, across many scientific fields, important phenomena can be understood in terms of complex systems and emergence. This framing provides a powerful context for exploring the relations between system components and aggregate behavior. In agent-based modeling approaches to complexity, a natural mapping between individual actions (agents) and emergent phenomena (aggregates) presents itself. In this domain, activities analogous to Distributed-by-Design activities have engaged learners in role-play to simulate complex systems and produce emergent outcomes (Wilensky & Stroup, 1999; Colella, 2000; Klopfer, Yoon & Perry, 2005).
Conclusion
viCollaborative software applications are becoming increasingly commonplace in educational settings, but often without accompanying tools or templates for effectively structuring collaborative learning activity. We see the combination of the MathNet software and the Distributed-by-Design strategy as a valuable model to guide other efforts along these lines. The distributed objects, views and tools showcase a range of possibilities and constraints in this design space. We are developing the MathNet platform as a free and open-source web-based platform with a flexible environment for authoring learning activities with the hope of building a community of mathematics educators and researchers who might join us in contributing to a growing library of lessons and materials, and in exploring the potential of these tools and a Distributed-by-Design approach.
References
viiBrady, C., White, T., Davis, S. and Hegedus, S. (2013). SimCalc and the Networked Classroom. In S. Hegedus & J. Roschelle (Eds.), Democratizing Access to Important Mathematics through Dynamic Representations: Contributions and Visions from the SimCalc Research Program (pp. 99-121). Advances in Mathematics Education Series, Springer.
CLICK Lab (Collaborative Learning in Classroom Networks) (undated) MathNet. Retrieved from: http://click.ucdavis.edu/designs/mathnet/
GeoGebra Enterprise (2018) GeoGebra. http://www.geogebra.org
Hardy, L. & White, T. (2016). Making sense of making waves: Co-constructing knowledge and group understanding without conceptual convergence. In C.-K. Looi, J. Polman, U. Cress, & P. Reimann (Eds.), "Transforming learning, empowering learners," Proceedings of the International Conference of the Learning Sciences (ICLS) 2016, (pp. 713-720). Singapore: National Institute of Education.
Moschkovich, J., Schoenfeld, A., & Arcavi, A. (1993). Aspects of understanding: On multiple perspectives and representations of linear relations and connections among them. In T. Romberg, E. Fennema & T. Carpenter (Eds.), Integrating Research on the Graphical Representation of Functions. (p. 69- 100) Hillsdale, NJ: Lawrence Erlbaum Associates.
About the Authors
viiiTobin White (University of California, Davis) studies the use of technology in teaching and learning mathematics. He has a particular interest in using mobile and networked computing to support novel approaches to engaging learners with STEM content and practices. Using a design-based research approach, he develops collaborative problem-solving tools and activities in order to investigate intersections between conceptual and social dimensions of learning. A former high school mathematics teacher, he has also worked for more than fifteen years in teacher preparation.
Corey Brady (Vanderbilt University) is Assistant Professor of Mathematics Education in the Department of Teaching and Learning at Vanderbilt University's Peabody College. Corey comes to Peabody from Northwestern University's School of Education and Social Policy, where he worked as a research assistant professor in learning sciences, engaging in design research to support and study math and science learning. Brady focuses on mathematical and computational modeling; on learning environments that foster representational fluency and expressivity; and on activities that promote collaborative and collective learning for classroom groups. He has also worked in industry, leading the design and development of Texas Instruments' TI-Navigator system (2001-2006), and he has been a classroom teacher at middle school, high school, and college levels.
WenYen Huang (University of California, Davis) is a doctoral student with an emphasis in Math Education. His research interest is utilizing advancements in technology to investigate ways for engaging students' motivation, enhancing students' understanding, and improving teachers' instruction in the mathematics classroom. WenYen earned a dual B.S. in Computer Science and Mathematics from Richard Stockton College of New Jersey, and M.Ed. in Mathematics Education from the University of Missouri - Columbia. He also taught a variety of Mathematics courses in Belton High School, MO for five years, including three years of college level courses.
Michael Stevens (University of California, Davis) is a doctoral student with an emphasis in mathematics education. His research interests are centered on how students are thinking mathematically in collaborative spaces through the use of technology. Michael earned his B.A. in Mathematics and his M.Ed. in Education from UC San Diego, and his M.A. in Educational Technology from CSU Sacramento. He is a former high school mathematics teacher and is currently teaching educational technology to multiple-subject teaching credential candidates.