Emergent Modeling: an RME Design Heuristic Elaborated in a Series of Examples
Eindhoven University of Technology

Abstract
The aim of this article is to offer an operational elaboration of the emergent modeling instructional design heuristic. This is one of the three instructional design heuristics with which the theory of realistic mathematics education (RME) may be characterized. First some background is given and it is elucidated how this heuristic was construed as a means of addressing the tension between RME theory and the socio-constructivist perspective on modeling. Next the heuristic is explicated in more detail with a design experiment on a sequence on addition and subtraction up to 100, which played a major role in the elaboration of this heuristic. Subsequently operational guidelines are presented, which are illustrated with reconstructions of the design of four instructional sequences, on addition and subtraction up to 20, introductory data analysis, graphs, and functions.
Introduction
In this paper we want to discuss one of the instructional design heuristics of the domain-specific instruction theory of realistic mathematics education (RME). Originally, RME was construed by Treffers (1987) as a descriptive theory. His primary aim was to distinguish the realistic approach from structuralistic, empiristic and mechanistic approaches. Later, however, RME has been characterized also with three instructional design heuristics: guided reinvention, didactical phenomenology and emergent modeling. In this article, we will focus on the latter design heuristic. In many publications emergent modeling has been described in terms of how it plays out in a given design or local instruction theory. An operational elaboration is lacking, however, and it is this lacuna this article aims to fill.
We will first discuss the background of this heuristic, then explicate the heuristic in more detail with an example that also played a major role in the elaboration of this heuristic. Next, we will seek an operational description, which will be applied to four different cases.
Instructional design heuristics
In 1987 Treffers published his framework of a domain-specific theory of mathematics education, which became known as realistic mathematics education, or RME. This framework was the result of reconstructing the theory underlying instructional sequences, which was based on Freudenthal’s (1973) ideas on mathematics education. As we noted above, this reconstruction had a descriptive character. Later, RME theory was recast in terms of three instructional design heuristics (Gravemeijer, 1999): guided reinvention, didactical phenomenology and emergent modeling.
Guided reinvention reflects Freudenthal’s (1973) idea that students should experience mathematics as a human activity and reinvent mathematics while being guided by teachers and tasks. The history of mathematics is an obvious source of inspiration for designing a route along which students might reinvent this mathematics.
Didactical phenomenology also originates from Freudenthal (1983). In his view, one of the main characteristics of mathematical activity is organizing—either organizing subject matter from reality or organizing mathematical matter on a higher level. The heuristic asks one to analyze what phenomena are organized, and how they are organized by the mathematical thought thing (concept, procedure or rule) one is aiming for. This then points in the direction of situations that may create the need for organizing such phenomena, and thus for inventing the appropriate thought thing.
The third heuristic is the emergent modeling design heuristic, which is the topic of this article. This heuristic aims at supporting an incremental process in which models and mathematical conceptions co-evolve. Central to the emergent modeling design heuristic is the use of a series of sub-models, which together substantiate an overarching model. This overarching model develops from a model of informal mathematical activity to a model for more formal mathematical reasoning.
Shortly after Treffers’ (1987) publication, (socio-)constructivism started to gain broad recognition in the mathematics education community. Socio-constructivist principles appeared compatible with Freudenthal’s (1973) notion that students should experience mathematics as an activity and construct mathematics by themselves—albeit guided by teachers and textbooks. Socio-constructivism was adopted in varying degrees by researchers working within RME. As a consequence - RME being a dynamic theory (Van den Heuvel-Panhuizen & Drijvers, 2014) - various conceptions of RME emerged, in which the role of (socio-)constructivism diverges.
A socio-constructivist elaboration (Gravemeijer, 2020) distinguishes itself from the earlier non-constructivist version in three aspects.
The socio-constructivist view on classroom culture; which translates into viewing an inquiry classroom culture as a prerequisite for enacting RME. This involves the classroom social norms, socio-mathematical norms, mathematical practices, and the corresponding teacher and student beliefs (Yackel & Cobb, 1996).
The way the mathematical practices are conceptualized. Here, framing mathematical issues as topics for whole-class discussions, plays a central role (Cobb, Gravemeijer, Yackel, McClain & Whitenack, 1997).
The notion of emergent modeling, which describes how a series of sub-models may support the mathematical advancement of students. How this heuristic reflects a socio-constructivist elaboration of RME is one of the topics of this paper.
The emergent modeling design heuristic
The emergent modeling design heuristic originated from frictions between RME and socio-constructivist thinking about the role of modeling. Where socio-constructivists were wary of the use of symbols and models, models played a central role in RME. Treffers (1987, p.246), for instance, designates, ‘bridging by vertical instruments’, such as, ‘models, schemas, diagrams and symbols’, as one of his five educational tenets. This bridging metaphor, however, conflicts with a constructivist point of view. This is because, as all knowledge has to be constructed by the individual, formal mathematics does not exist as an external body of knowledge independent of a knowing actor. Thus, for the students there is nothing this bridge can connect with. Moreover, the use of models and symbols was seen as problematic in general. Classroom observations had shown that teachers failed to convey mathematical knowledge by using symbols and models. This was explained by arguing that symbols and models did not signify for the students what they signified for the teachers, as a model or symbol does not carry meaning in-and-of-itself. Or, to be more precise, inscriptions—marks on paper or tactile objects—do not carry meaning. The word ‘symbol’ is less precise. It might mean merely the inscription, but it might as well refer to a broader conception, including its meaning in a given social practice. We will, however, use kindred terms flexibly.
Speaking of the meaning of symbols, Bereiter’s (1985) learning paradox comes to mind, which we may phrase in the following manner. In order to gain access to a given piece of mathematics, students need to understand the symbols that belong to that piece of mathematics. However, these symbols derive their meaning from the very piece of mathematics the students are trying to get access to.
A way to circumvent the learning paradox was found in the emergent modeling design heuristic (Gravemeijer, 1999). Instead of telling students how they should interpret a given model, or symbolization, one would aim for an incremental process in which models are constructed. Central to the emergent modeling design heuristic is the use of a series of sub-models, which build on each other. This idea of a series of sub-models proved similar to the way symbolizations developed in the history of mathematics. Historically, formal symbolizations grew out of informal, situated, forms of symbolizing. They developed over time in a reflexive process in which symbolizations and meaning co-evolved (Meira, 1995; Latour, 1990). This reflexive process involves a cyclic alternation of developing new symbolizations and developing new meaning. Working with certain symbolizations, one’s conceptual understanding deepened, then new symbolizations were developed that captured the new meaning and working with the new symbolizations started a new cycle. In relation to this, we speak of a ‘chain-of-signification’ (Walkerdine, 1988).
Addition and subtraction up to 100
The emergent-modeling idea originated from noticing a shift in the thinking of students, who were using the so-called empty number line; from modeling calculations that mirrored actions in the context of the problem, to modeling the use of number relations, which did not mirror the activity in the problem context (Gravemeijer, 1991). Here we may think, for instance, of a task such as:
Jim had 66 sweets. He has eaten 39 of them.
How many sweets does he have now?
The corresponding calculation would be ‘66 take away 39’, which could be solved by counting down in jumps on the empty number line. Figure 1a shows the jumping as 66 – 6 = 60; 60 – 30 = 30; 30 – 3 = 27. However, the problem may also be solved by reasoning, 66 – 39 = 66 – 40 + 1 = 27 (Figure 1b), using the number relation 39 = 40 – 1.
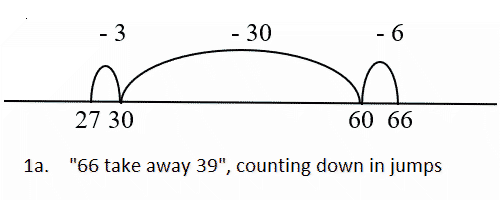
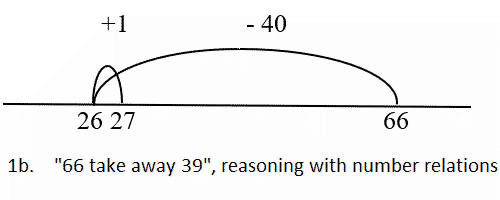
This difference was interpreted as a shift in what the model signified for the students. Initially the model signified potential actions in the problem context; later the model signified reasoning with number relations. Key in this transition is that the students developed a network of number relations. Only because the students had constructed the relevant number relations, could they use the number line as a model for reasoning about number relations. This observation laid the basis for the emergent modeling design heuristic, which assumes that a model of informal mathematical activity may develop into a model for more formal mathematical reasoning.
This emergent modeling instructional design heuristic was worked out during a design experiment with a local instruction theory on addition and subtraction up to 100 in the context of linear measurement (Stephan, Bowers & Cobb with Gravemeijer, 2003). A local instruction theory encompasses the tasks, discourse, social norms, tools and the orchestration of the classroom discourse (Gravemeijer, 1991). With an eye on readability, however, we will limit ourselves to tasks and tools and use the term ‘instructional sequence’. The design encompasses a series of sub-models or tools, which originate from iterating individual measurement units, and develop into the more abstract jumps on the empty number line—which students use to scaffold the activity of adding and subtracting numbers up to 100. We will start by briefly summarizing the series of sub-models.
- After some introductory activities a start is made by measuring length by iterating Unifix cubes (in the context of a story of dwarfs measuring with food cans the size of one Unifix cube).
- After that a ten bar (ten Unifix cubes clicked together) is introduced to facilitate the measuring activity. The students then have to coordinate units of ten and one.
- Soon thereafter the ten bar is replaced with a paper ten strip, which is more convenient for the dwarfs. In order to measure with just the strip—without loose cubes—units of one cube have to be marked on the paper strip (see Figure 2).
- Next 10 ten strips are glued together, generating a measurement strip of 100 units (see Figure 2).
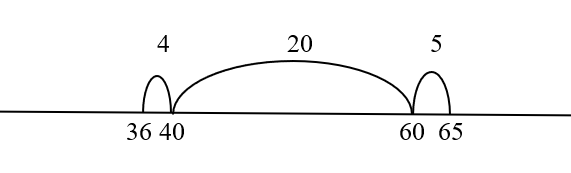
- Then activities involving incrementing, decrementing and comparing lengths are presented to the students. Those tasks may be solved by counting individual units on the measurement strip at first, but the students may also start using the measurement strip for scaffolding arithmetical solution methods. For example, the difference between 36 and 65 is found by adding 4 to 36 to get 40, then adding 20, which makes 60, and finally adding 5 to 60 to get to 65—which corresponds with a difference of 4 + 20 + 5 = 29.
- It is at that moment that jumps on the empty number line are introduced as means of scaffolding and communicating arithmetical solution strategies (Figure 3). This anticipates using number relations without the support of a number line.

Sub-models and an overarching model
Within this series of sub-models or tools, actions with a new tool signify actions with an earlier tool for the students. In this respect we can speak of a ‘chain-of-signification’ (Walkerdine, 1988). Thus, there is always a history which allows for a sensible interpretation of the activity with the new tool. Each time, the introduction of a new tool is accompanied by new student activity.
A number of comments may be made here. The first is the caveat that, when designing an instructional sequence, the tools are invented by the instructional designer, not by the students. To adjust for this one may try to ensure that each new tool emerges as a solution to a problem that has its roots in activity with the earlier tool. In this manner, the history of working with the earlier tool may provide the imagery underlying the new tool. Whether this is the case may be inferred from whether or not the new tool is used flexibly by the students.
As a second comment we may note that, although we use the outer forms to identify the sub-models, the term ‘model’ has to be understood in a much broader sense. We are not just referring to a visual or tactile representation, but to what it signifies for the students in the corresponding social practice; this encompasses the history, the activity with the model, and the purpose of that activity.
A last comment is that the goals for the students differ from the goals for the teachers and instructional designers. The activity itself may be the goal for the students whereas the goal for the teacher/instructional designer concerns the mathematical issue that is addressed in the activity. (See Table 1, adapted from Gravemeijer, Bowers & Stephan (2003)). We may especially point to the goal of coordinating units of 10 and 1, and the activities on incrementing, decrementing and comparing lengths, which foster the development of number relations, especially involving multiples of ten.
|
Tool |
Imagery/history |
Activity |
Mathematical Issues |
|---|---|---|---|
|
Food cans |
Measuring by iterating a Unifix cube, or by creating a stack of Unifix cubes |
||
|
Ten bar |
Signifies result of iterating |
Measuring by iterating a collection of ten cubes |
Coordinating measuring with 10s with measuring by 1s |
|
Ten strip |
Signifies measuring 10s and 1s with the ten-bar |
Measuring by iterating the ten strip, and using strip as a ruler for the 1s |
Coordinating units of 10 & 1 |
|
Measurement strip |
Signifies measuring with ten strip; strip starts to signify result of measuring |
Measuring with measurement strip by reading of endpoints Reasoning about spatial extensions; incrementing, decrementing and comparing lengths |
Distance seen as already partitioned; extension already has a measure Developing and using number relations |
|
Jumps on the empty number line |
Signify reasoning with measurement strip |
Using the empty number line as a means of scaffolding & communicating about reasoning about number relations |
Constitution of numbers as mathematical objects that derive their meaning from number relations |
The notion of a ruler may be conceived as the overarching model. The ruler emerges as a model of iterating one or more measurement unit(s), and gradually evolves into a schematized ruler, which becomes a model for reasoning about flexible mental-arithmetic strategies for numbers up to one hundred. Within this transition we may distinguish four levels of activity (Gravemeijer, Cobb, Bowers & Whitenack, 2000):
- situational activity; activity in the task setting; measuring by iterating one or more measurement unit(s)
- referential activity; activity with a measurement strip, respectively empty number line, based on the imagery of iterating some measurement unit
- general activity; using the model to support reasoning with number relations
- formal mathematical reasoning; the activity of reasoning with number relations independent of some model.
We may add that the model-of/model-for transition in the emergent modeling design heuristic has to be understood in a metaphorical sense. It is a construct which helps the instructional designer to think about the emergent modeling process. The students work with the series of symbolizations or sub-models, which can be seen as a material correlate of ‘the model’.
We further reiterate that the emergent modeling process not only fosters the development of meaningful symbolizations or models; it also fosters the students’ mathematical advancement. Consequently, the ‘model-for’ derives its meaning from a different reality (for the students) than the ‘model-of’. We may illustrate the constitution of some new mathematical reality by looking at the change in what numbers signify for the students. Initially numbers signify magnitudes; they are tied to measurement units (i.e. food cans). In the end numbers signify mathematical objects that derive their meaning from number relations, e.g. 45 is associated with 45 = 40 + 5; 45 = 30 + 15; 45 = 65 – 20 and so forth. In summary, we may describe the change in terms of three intertwined transitions: (1) the series of sub-models, (2) the transition from a model of iterating one or more measurement units to a model for reasoning about number relations, (3) the constitution of new mathematical reality; from measures to numbers as objects within a framework of number relations.
From informal to more formal
As a final point we want to discuss the use of the word ‘formal’. Formal might be associated with bare ‘sums’, or with ready-made mathematics. That is not what is meant here. What we have in mind here, is mathematics that is constructed by the students by mathematizing their own informal mathematical activity. The distinction ‘formal – informal’ is made from the perspective of the instructional designer. The goal of the emergent modeling approach—and of RME in general—is that the students do not experience more formal mathematics as different from informal mathematics. In relation to this, Freudenthal (1991) speaks of growing common sense. Mathematics should start within, and stay within, the growing common sense of the student. He notes that what is common sense to a mathematician differs from what is common sense to a student. He links common sense to his conception of reality in the following manner: ‘I prefer to apply the term ‘reality’ to that which at a certain stage common sense experiences as real’ (Freudenthal, 1991, p.17). This implies that our reality expands when what we experience as common sense grows. In this respect, Freudenthal’s conception of reality appears to be compatible with (socio-) constructivism, even though he spoke out against it (Freudenthal, 1991, p. 17). We may argue that the latter was more the result of an incorrect image of (socio) constructivism, than a difference in epistemology. Ideally the students’ growing reality should also encompass mathematics. Following this line of reasoning, learning mathematics may be described as constructing a new piece of reality. In relation to this Freudenthal speaks of the creation of new subject matter:
At every level the subject matter is a certain field that will be organized on this level. The devices of organizing on a certain level will form the field and therefore the subject matter, on the consequent higher level. (Freudenthal, 1957, cited by La Bastide-van Gemert, 2015, p. 192)
This idea of organizing and creating new subject matter seems in line with Sfard's (1991) characterization of the dual nature of mathematics, which involves turning processes into objects, which in turn are used in new processes.
La Bastide-van Gemert (2015) elucidates that Freudenthal builds on Van Hiele’s (1973) theory. Van Hiele offered a theory about how students could construct more sophisticated mathematics by constructing networks of mathematical relations. Against this background, we may connect the progression from informal to more formal mathematical reasoning with the creation of some new mathematical reality consisting of mathematical objects within a framework of mathematical relations. Thus, the distinction between ‘model-of’ and ‘model-for’ is not tied to specific manifestations of the model. Instead, it relates to the student’s thinking, within which ‘model-of’ refers to an activity in a specific setting or context, and ‘model-for’ to a framework of mathematical relations—i.e. an emerging new mathematical reality.
This new mathematical reality corresponds with the body of mathematical knowledge that we identified as the central problem when discussing the bridging metaphor earlier. Thus, instead of trying to help students to make connections with a body of mathematical knowledge that does not (yet) exist for them, the emergent modeling approach helps students in constructing this mathematical reality/ body of knowledge by themselves.
The latter delineates how the mantra ‘from model-of to model-for’ has to be understood. The phrase ‘from model-of to model-for’ is not uncommon. When talking about models, one will soon use the words ‘model of’ and ‘model for’. This also is the case in earlier RME literature. What is key in the emergent modeling design heuristic, however, is not the terminology, but the way it pairs modeling to the construction of a network of mathematical relations. The idea of supporting students in construing new reality, comprised of mathematical objects and a network of mathematical relations, differentiates the emergent modeling design heuristic from conceptions of models and modeling in earlier RME literature—including Streefland (1985).
We may note that van den Heuvel-Panhuizen (2003) seems to have overlooked this difference, when emphasizing the role of Streefland (1985) as the originator of the idea of a ‘from model-of to model-for’ shift. Moreover, the expressions ‘model of’ and ‘model for’, are not salient in Streefland’s (1985) article. He mainly uses this wording while explaining his idea of a model as an ‘after-image’, which may become a ‘pre-image’ for organizing or working similar or new problem situations. The latter typology, however, never caught on.
Using emergent modeling in design experiments
The emergent modeling design heuristic has been used in design experiments on various instructional topics (listed in the Appendix). However, even though emergent modeling as an instructional design heuristic has been used repeatedly, an operational description is still lacking. In part, such an operational description may be deduced from the discussion of the example on the addition and subtraction to 100 presented earlier. As students have to be supported in developing mathematical relations in order to reach the intended goal of constructing mathematical objects, one of the first actions of the designer will have to be to identify which mathematical relations have to be developed. Similarly, starting points in terms of situations that are experientially real to the students have to be identified. And, last but not least, a series of sub-models that together constitute some overarching model have to be found.
Footholds for the design strategy
We may use such considerations to work out how an instructional designer could build on the work and research that already has been done in a given domain. This may concern, for instance, what is known about informal solution strategies, and what it means to be proficient in this domain. Also, manipulatives, schemas or models that are commonly used may be taken into consideration. Their strengths and weaknesses should be examined, considering if and how they might be adapted. Following this line of reasoning, we can operationalize the emergent modeling design heuristic with the following more detailed guidelines.
-
Identify the instructional goals
Look at informal solutions and the solutions of proficient students—which may overlap—to define goals that can be described as objects or as networks of mathematical relations.
-
Identify a central sub-model
Take stock of the models, manipulatives, and inscriptions that are being used in the domain under consideration, to create a source of inspiration for the design/choice of a central model.
-
Identify instructional starting points
Look for contextual problems that are experientially real to the students and can be modeled with the central model.
-
Design a series of sub-models and identify the overarching model
Situate the central model in a series of sub-models and look for characteristics of the series of sub-models, which may constitute the overarching model.
-
Reflect on the sequence from the perspective of:
-
- the chain-of-signification
- the model-for/model-of transition
- the creation of new mathematical reality.
-
We will elucidate these guidelines below. For each guideline, we will offer a brief description of how this guideline would pan out for the design of the sequence for addition and subtraction up to 100 we just discussed.
1. Identify the instructional goals
When designing an instructional sequence, one has of course some instructional goals in mind. The emergent modeling heuristic, however, aims at a specific kind of goals; goals in terms of mathematical objects, or networks of mathematical relations. The heuristic therefore asks the designer to consider what the goals of the sequence might look like in terms of mathematical relations or objects. A useful approach often is looking at what is known about the informal strategies that students invent by themselves.
As instructional goals for the sequence addition and subtraction up to 100 we may point to structuring numbers in terms of 10s and 1s, decuples-related number relations and number relations up to 20, in connection with the construction of the corresponding mathematical objects.
2. Identify a central model
For many topics there are already tactile or visual models in use. Often these models are presented to the students in a ready-made form, and often the interpretation of the model as signifying the intended mathematics is erroneously considered self-evident. Still, such models often can serve as a starting point for designing a series of sub-models within an emergent modeling heuristic. This is done by adapting the model and considering how such an adapted model might emerge from meaningful student activity and considering how working with this kind of model might support students in constructing the intended mathematical relations and objects.
Looking for a central model for addition and subtraction up to 100, it is natural to think of the number line model, which is commonly used as a means of support. New in the design for the sequence up to 100 was the idea of using an empty number line, which was proposed by Whitney (1988), and adopted by Treffers (1991a).
3. Identify instructional starting points
One of the core elements of emergent modeling is that models do not appear from thin air but emerge from modeling contextual situations that are experientially real to the students. Thus, one of the tasks of the instructional designer is to identify such starting points. In other words, knowing the central model, one has to look for situations that are experientially real and could be modeled with this model, or an adaption thereof. In relation to this, one may consider applications of the mathematics under consideration with an eye on their potential usefulness as starting points.
As instructional starting points Whitney (1988) and Treffers (1991a) chose activities involving counting beads on a bead string with 100 beads with alternating groups of ten dark and ten white beads. This was replaced by linear measurement in the aforementioned teaching experiment, in order to support the coordination of the cardinal and the ordinal number aspect. The cardinal aspect is reflected in the individual measurement units that are counted when measuring. The ordinal aspect comes to the fore in the numbers on a ruler which each indicate a corresponding length. Freudenthal (1983) also argues for this combination on basis of a didactical-phenomenological analysis. He further adds that measures play a bigger role in society than quantities.
4. Design a series of sub-models and identify the overarching model
Similar to considering a careful introduction of the model, the transition from using the model towards working without a model, or working with standard mathematical notations, has to be planned carefully.
The sub-models and overarching model of the aforementioned sequence follow in a natural manner from the choice for linear measurement.
5. Reflect on the sequence
In conclusion, we may reflect on how the series of sub-models, the model-of/model-for transition and the creation of new mathematical reality, hang together. Here a table—such as Table 1—listing how the tools/sub-models, imagery/history, activity, mathematical issues evolve, may prove helpful. The overview of the sequence for addition and subtraction up to 100, which is asked for under the heading ‘reflection’, is clearly elaborated in Table 1.
In the following we will take four separate examples of emergent-modeling-based sequences to show how they might have been designed with help of the aforementioned guidelines:
It is not necessary for the reader to engage with each of these examples in sequence; a selection can be made.
Addition and subtraction to 20
The first example of how the above guidelines might be used concerns a sequence on addition and subtraction up to 20. For this example, we draw on another design experiment that was carried out in Nashville, USA (Gravemeijer et al., 2000).
1. Identify the instructional goals
Research shows that proficient students develop strategies that make use of the doubles, and fives and tens as points of reference, as in ‘7+8=5+5+2+3’, or ‘7+8=14+1’, or ‘7+8=7+3+5=10+5’ (Van Eerde, 1996). We may argue, however, that these students are not consciously applying strategies such as ‘filling ten’, ‘using doubles’, or ‘using five as a reference point’. Instead, it seems more likely that the students combine number facts, which are ready to hand to them, to derive new number facts. When having to solve ‘7+8=…’, for instance, various number facts may come to mind. The students may, for instance, think of: ‘7+3=10’, ‘8=5+3’, ‘8=7+1’, ‘7=5+2’, ‘7+7=14’, and ‘8+8=16’. Combining some of those number facts, they may come up with ‘7+8=5+5+2+3’, or ‘7+8=14+1’, or ‘7+8=7+3+5=10+5’, as ways to calculate 7+8. On basis of this analysis we decide to support students in developing sets of more basic number relations—especially five- and ten-referenced, and doubles—and foster the flexible use of those number relations to derive new number facts when solving additions or subtractions up to 20. Thus, the goal of an instructional sequence on addition and subtraction up to 20, may be conceived as students developing networks of number relations, and using them flexibly when solving addition and subtraction problems.
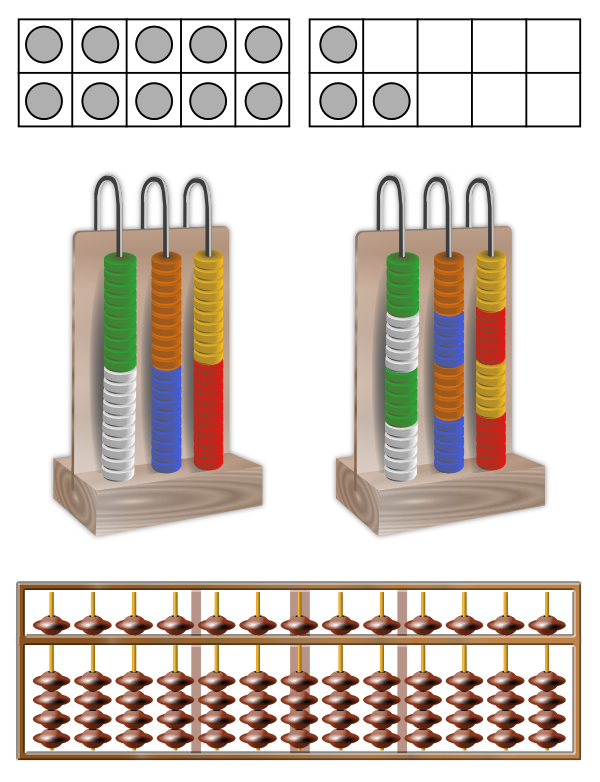
Enlarge…
2. Identify a central model
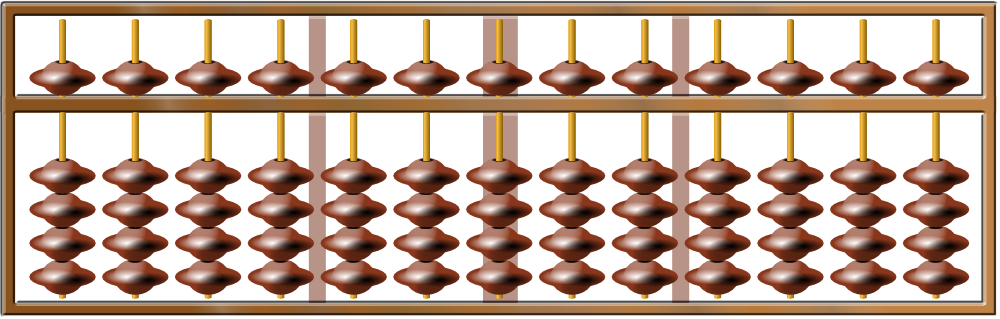
Searching for ways to model addition and subtraction up to 20, manipulatives shown in Figure 4 such as ten-frames, the school abacus, and the soroban come to the fore as sources of inspiration.
The designer’s task then is to think of how working with one of these models might foster use of the doubles and fives and tens as points of reference when solving addition and subtraction problems up to 20. The ten-frame, for instance, might foster the use of doubles, five- and ten-referenced number relations for numbers up to ten. The number of chips in the ten-frame in Figure 4a can be construed as double 3 plus 1, or double 4 minus 1. It can also be seen as 10 minus 3, or 2 + 5 if you imagine moving one chip. As variation on the ten-frame, one might think of a double ten-frame ( Figure 4b) to also include numbers from 10 to 20.
4a: Ten Frame
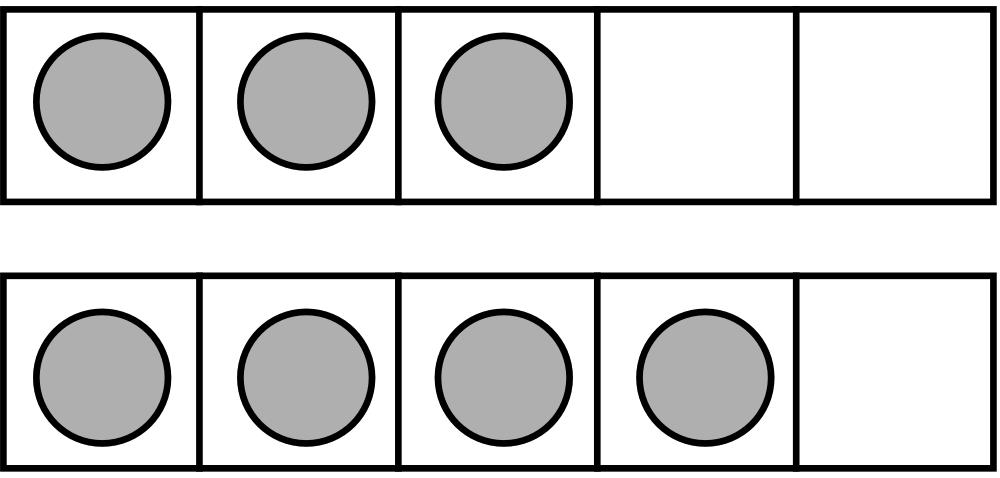
4b: Double ten frame showing 6 + 7

4c: School abacus

4d: School abacus with five structure

4e: Soroban
Enlarge…
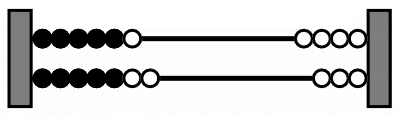
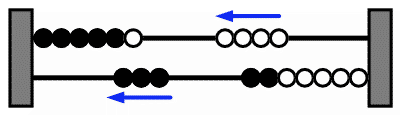
Treffers (1991b) invented the so-called arithmetic rack, which is somewhat similar to the double ten-frame. It consists of two bars with five dark and five white beads on each bar. Students can visualize numbers on the rack by shifting beads to the left, with the beads on the left representing the intended number ( Figure 5).
An advantage of the rack is that there are no loose pieces that may fall on ground, while it still allows for various solution methods. One may for instance, represent two numbers independently on the upper and lower bar and find the total, or start with one number and shift beads to fill up the upper rod, continue on the lower rod and then find the total. The idea is that students do not just count the beads one by one but take advantage of the structure of the rack. Once they have put the numbers on the rack, the rack offers a scaffold for number relations they used when putting the beads on the rack. Having used 6 = 5 + 1 and 7 = 5 + 2 to visualize 6 and 7 on the upper and the lower bar respectively, they may use those number relations to find the total; (5 + 1) + (5 + 2) = 10 + 3 = 13 (see Figure 5).
Later on, students will be asked to think about the manner in which they want to put the beads on the rack, before actually putting them on; anticipating how they are going to use the corresponding number relations. In this manner the teacher may ensure that the students use the rack as a tool for thinking and not as a primitive calculator. When solving 6 + 7, for instance, students may anticipate using 6 = 5 + 1, and 7 = 5 + 2, in order to build on 5 + 5 = 10 to calculate 6 + 7 as 5 + 5 + 1 + 2 = 13 (Figure 6a). They might also anticipate using 6 + 6 = 12, and reason that 6 + 7 = 12 + 1 (Figure 6b). Or they may reason, 6 + 4 = 10, and 7 = 4 + 3, thus 6 + 7 = 13 (Figure 6c).
6a. 6 + 7 = 5 + 5 + 1 + 2

6b. 6 + 7 = 6 + 6 + 1
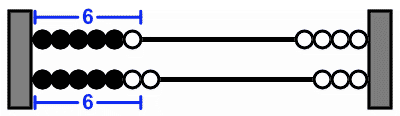
6c. 6 + 7 = 6 + 4 + 3
The arithmetic rack appears to be a perfect candidate for functioning as a central model in an emergent modeling design on addition and subtraction up to 20. This sub-model has to be complemented with activities that would support the linkage of the students’ reality on the one hand with the more formal mathematics on the other hand.
3. Identify instructional starting points
Treffers (1991b) already recognized the need for a meaningful introduction of the arithmetic rack. He chose to use the context of varying numbers of passengers in a double-decker bus. (Others also used contexts such as monkeys in two trees (Cobb, Boufi, McClain, Whitenack, 1997), or students in bunk beds (Fosnot, 2008).) Students could use the arithmetic rack to keep track of the number of passengers on the upper and lower decks by putting the corresponding number of beads on the upper and the lower bar. Next, problems could be posed, where the students themselves could decide how the numbers would be distributed over the two bus decks (two bars). Once the students are familiar with the arithmetic rack, number tasks without context can be assigned.
4. Design a series of sub-models and identify the overarching model
Similar to the care taken in introducing the model, the transition from using the model towards working without a model, or working with standard mathematical notation, has to be planned carefully. This step was worked out in the teaching experiment in Nashville, in which we introduced a more schematized way of notating one’s reasoning when working with the arithmetic rack as the next step (see Figure 7) (Gravemeijer et al., 2000). Ideally, of course, the students would have to invent this more formal way of symbolizing. For practical reasons, however, a symbolic way of notating was introduced casually by the teacher when discussing students’ solutions. These actions are subsequently notated as bare ‘sums’.
The teacher did not comment on inscriptions she made on the blackboard. Later she asked the students to come up with their own ways of describing their reasoning on paper. The students used variants of what they had seen on the blackboard.
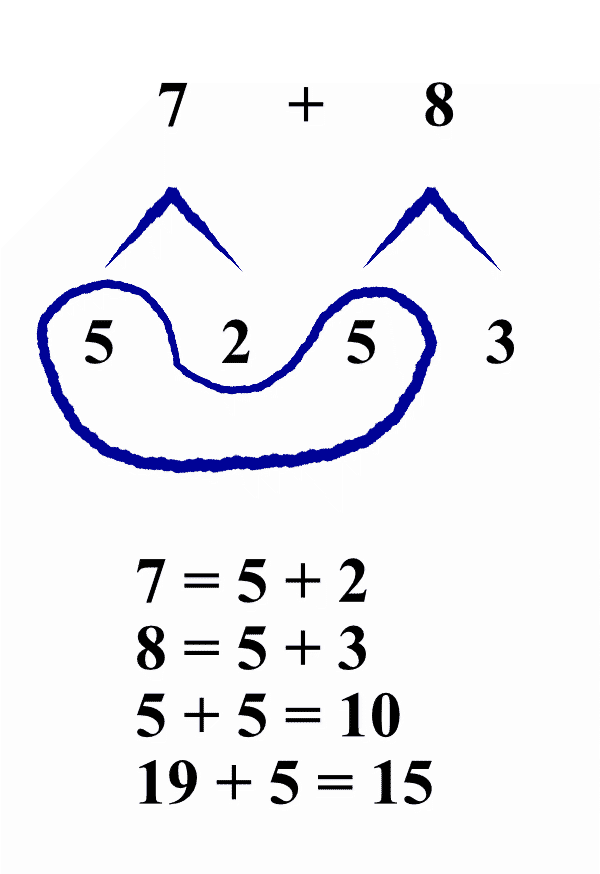
This symbolic notation shows:
5 + 2 beads to represent 7 on the top rod and
5 + 3 beads to represent 8 on the bottom rod.
Then taking the two 5s togather and adding the remaining white beads.
5. Reflect on the sequence
The chain-of-signification (series of sub-models) is described in Table 2.
|
Tool/inscription |
History/imagery |
Activity |
Mathematical issues |
|---|---|---|---|
|
Double-decker bus |
Keeping track of the number of passengers |
||
|
Arithmetic rack |
Passengers on a double-decker bus |
Calculating the number total or remaining number of passengers |
Developing and using doubles-related, and five- and ten-referenced number relations |
|
Symbolic descriptions |
Beads on the arithmetic rack |
Describing addition strategies with beads on the arithmetic rack |
Developing and using doubles-related, and five- and ten-referenced number relations |
In retrospect we note that the students initially describe a contextual situation of passengers on a double-decker bus. Then the configuration of beads on the arithmetic rack is used to describe what happens in the context of the task, and it functions as a model-of (reasoning about) the distribution of the passengers in the bus. Subsequently—under guidance of the teacher—the attention of the students gradually shifts towards the number relations involved, and how they can be used. As more number relations are being formed, actions on the arithmetic rack start to signify for the students the ways of reasoning with those number relations, and thus becomes a model-for more formal mathematical reasoning. This transition is further supported by the introduction of the symbolic form of Figure 7. Over time the students may become so proficient that they will not need visual scaffolding anymore. The students then reach the level of more formal mathematical reasoning.
When zooming out, we may see the sequence as part of a transition from an operational conception to a structural conception (Sfard, 1991). This encompasses the transition from processes, such as counting and structuring quantities, to the constitution of numbers as objects that derive their meaning from a network of number relations.
Introductory Data Analysis
For the next example, designing a sequence on introductory data analysis, we draw on a third design experiment that was carried out in Nashville (Gravemeijer & Cobb, 2013).
1. Identify the instructional goals
Enlarge…
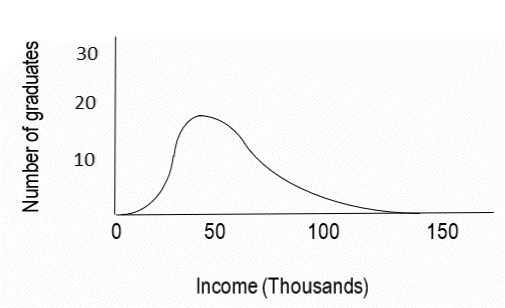
The choice of goals is determinative for the introductory data analyses sequence. Common goals concern the measures of central tendency and standard visualizations. However, when aiming for goals in terms of mathematical objects and a network of mathematical relations a different goal comes to the fore, namely that of ‘distribution’ as an object. The line of reasoning here is that mean, mode, median, quartiles, extremes, and the various visualizations are all invented as means of characterizing a distribution of the datapoints. These instruments can be reinvented while developing the notion of a distribution as an object. This object may be conceptualized by the designer as a density function; a function that describes the density of data points for a range of measurement values. This density function may be depicted as a curve, such as the bell-curve for a normal distribution or the skewed curve shown in Figure 8. The network of relations encompasses data points and density but also skewedness, spread, position, measures of central tendency and visual representations.
Enlarge…
2. Identify a central sub-model
The central model logically involves the distribution of data points. And thus, the dot plot presents itself as a self-evident choice for the central model.
3. Identify instructional starting points
When looking for experientially real starting points, we may consider that data find their origin in measuring. We may assume that students are familiar with scale lines and bar graphs as ways of representing data. It may further be argued that variables with a linear or temporal character lend themselves in a natural way for visualizing values with line segments. In the Nashville experiment this was worked out in the task of comparing data on two brands of batteries, in service of a consumer report. Instead of giving students the raw data, however, the data were embedded in a computer tool, Minitool 1, in which each measure is represented by a bar (Figure 9). A slide show demonstrating the tool is found at: www.fisme.science.uu.nl/toepassingen/28848/images/diashowminitools.html
4. Design a series of sub-models and identify the overarching model
The sub-models have to connect the initial way of representing data with the dot-plot representation, and the latter with a more sophisticated model of a distribution. The transition from individual bars to a dot plot can be made by imagining the endpoints of the bars dropping on the horizontal axis. The value-bar representation shown in Figure 10, would then turn into the dot plots of Figure 11.
Click to enlarge
Tasks on comparing data sets might facilitate this, as this would focus the attention on the endpoints of the bars. Subsequently, the focus may shift to how the density of data points is distributed over the range of measurement values (in this case, the horizontal axis). Hereto a second computer tool, Minitool 2, was designed, which allowed for structuring data sets represented as dot plots. This is also demonstrated in the slide show.
To foster the transition to a more sophisticated representation such as a box plot, the computer tool facilitated introducing vertical bars splitting the data sets in two or four equal groups (see Figure 12).
Click to enlarge
Working with those tools, the students might start to realize that the data-density is bigger where the vertical bars are closer to each other. At the same time, the students are expected to start talking in terms of the shape of the distribution. Key here is that the students come to see that, in many data sets, the median is a good indicator of where the data is clustered. The four equal groups representation may function as a precursor for the box plot (see Figure 12). In the box plot, the central vertical line shows the median, and the boxes and the whiskers showing how the data points are spread out. Thanks to this history, the box plot may come to signify the shape of a distribution for the students (Figure 13). In this way the box plot may become a tool for reasoning about skewness, spread and position.
In retrospect, we may notice that this sequence also could have been found by using Freudenthal’s (1983) Didactical Phenomenological Analysis, which advises the designer to analyze what phenomena are organized by the concept, tool or procedure you are aiming for. Thus, the question would be: what phenomenon is organized by a density function? This question might be answered with ‘density’. Simultaneously, density organizes ‘data points on an axis’. In turn, the representation of data points on an axis organizes measurement values.
Given the sub-models that come into play, we may describe the overarching model as ‘the graphical representation of the shape of a distribution’.
5. Reflect on the sequence
As with the other examples, we see three intertwined transitions. The first evolves along the series of sub-models; value bars, dot plot, four equal groups, and box plot. Table 3 shows how these sub-tools build on each other. Table 3 also shows what mathematical issues correspond with the various activities the students engage in. The second concerns the shift from a model of a set of measures to a model for reasoning about distributions (as objects). The third involves the constitution of new mathematical reality in which distributions exist as object-like entities.
|
Tool/inscription |
History/imagery |
Activity |
Mathematical issues |
|---|---|---|---|
|
Measures |
Talking through the process of data creation |
Doing data analysis for a reason |
|
|
Set of value bars |
Measures |
Describing and comparing data sets |
Lengths signifying measures Measures as values of a variable Horizontal axis signifying values of a variable Shape of the distribution |
|
Dot plot |
Set of value bars |
Describing and comparing data sets |
Shape of the distribution Heights of stacked dots signifying density |
|
Dot plot split into four-equal groups/box plot |
Set of (endpoints of) value bars |
Describing and comparing data sets |
Distribution as an object; position, skewness, narrowness Shape of the distribution Widths of bins correspond inversely with density Distribution as an object; position, skewness, narrowness |
Graphs
In anticipation of the example of functions, we will first discuss a sequence on graphs. In our view, graphs – which are an essential component of functions – warrant an independent sequence. Graphs and graphing are less straightforward than often presumed. It is often overlooked that what we can infer from graphs is dependent on some hidden conventions. Associating slope with ascending, descending or constant function values may be just a language game for many students, which is not grounded in understanding why and when the steepness of a graph relates to adjacent function values. We argue therefore that students have to reinvent graphing as a tool for analyzing relations between two variables. In our exposition on how the guidelines might be applied for designing a sequence on graphs we primarily draw on a series of design experiments by Van Galen and others on graphing (see for instance, Van Galen & Gravemeijer, 2010; Van Galen & Markusse, 2018). These were carried out in the Netherlands.
1. Identify the instructional goals for graphs
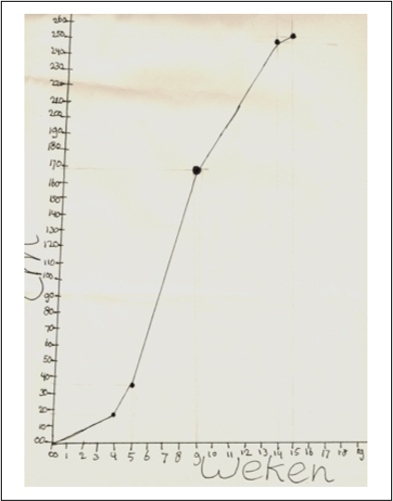
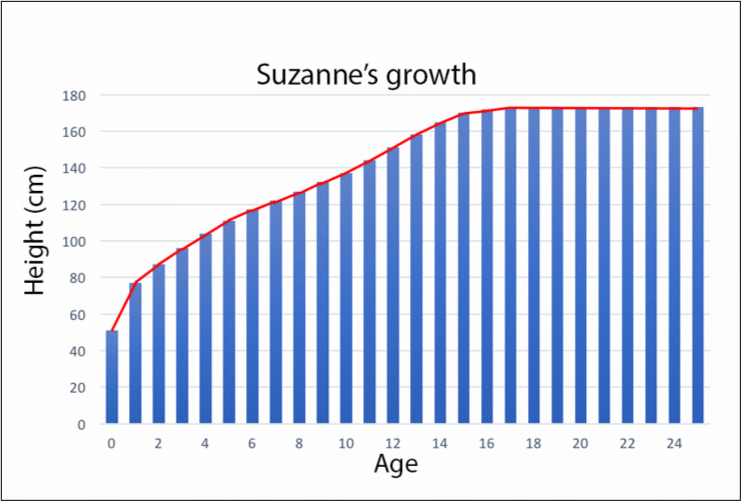
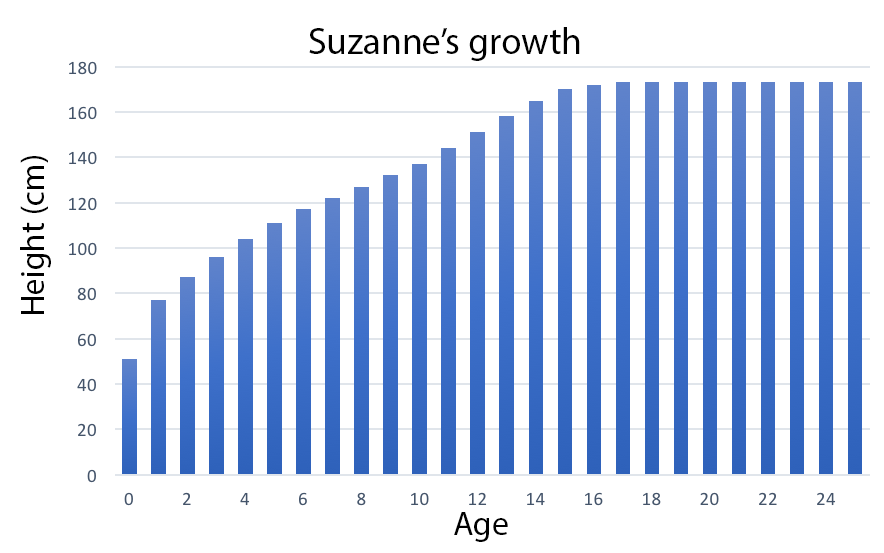
The mathematical relations that underpin Cartesian graphs are hidden in conventions. These conventions, for instance, concern the proportional way variables are mapped on the axes. They also involve interpreting a point on the Cartesian plane as a number pair signifying two connected measures. Moreover, students have to make the shift from measures as attributes to measures as values of a variable (Jones, 1971). Initially, students see measures as attributes e.g. 174 cm is the length of Suzanne. In order to be able to reason about the relation between length and time, however, students have to see measures as potential values of a variable that can vary over a certain domain. Moreover, students have to conceptualize graphs of continuous data as objects that can be interpreted dynamically.
Enlarge…
2. Identify a central sub-model
A simple graph may consist of a series of bars signifying individual measures at distinct points in time (Figure 14). We may take this as the central sub-model, which has to be connected with experientially real starting points on the one hand, and graphs of continuous data on the other hand.
Enlarge…
3. Identify instructional starting points
Tasks on depicting growth, time or speed, are rather common as a way of introducing cartesian graphs. Here one may assume that students are familiar with depicting individual measures such as lengths, e. g. when working with scale lines, or case-value bar graphs. (One might also start earlier by developing bars as representations of magnitudes.) Then the context of depicting the growth of a person or a plant on the basis of pairs of time and height data, might be considered experientially real for the students. Similarly, the context of depicting distances traveled in fixed time intervals with paper strips might be experientially real for the students.
4. Design a series of sub-models and identify the overarching model
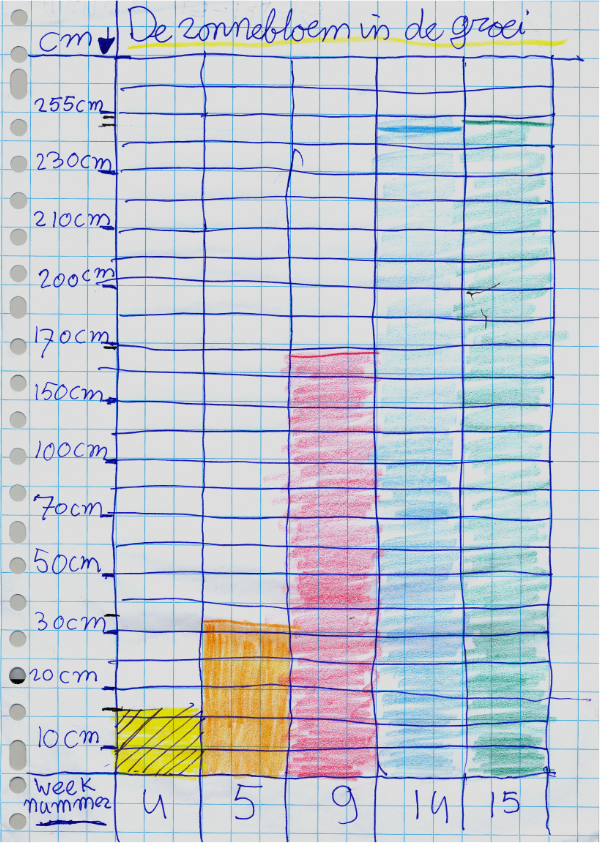
Here we follow Van Galen and Gravemeijer (2010), who chose an initial task of depicting the growth of a sunflower over a period of time with a data set that included irregular intervals. Many students initially made nice drawings of a series of sunflowers, but later realized that they could suffice with bars or even lines that showed the heights. As might be expected, not all students used proportional axes. The first sub-model may therefore be thought of as graph-like pictures in which the proportionality of the axes is not a given. An example is shown in Figure 15, where neither the vertical axis (height) nor the horizontal axis (weeks) are proportional.
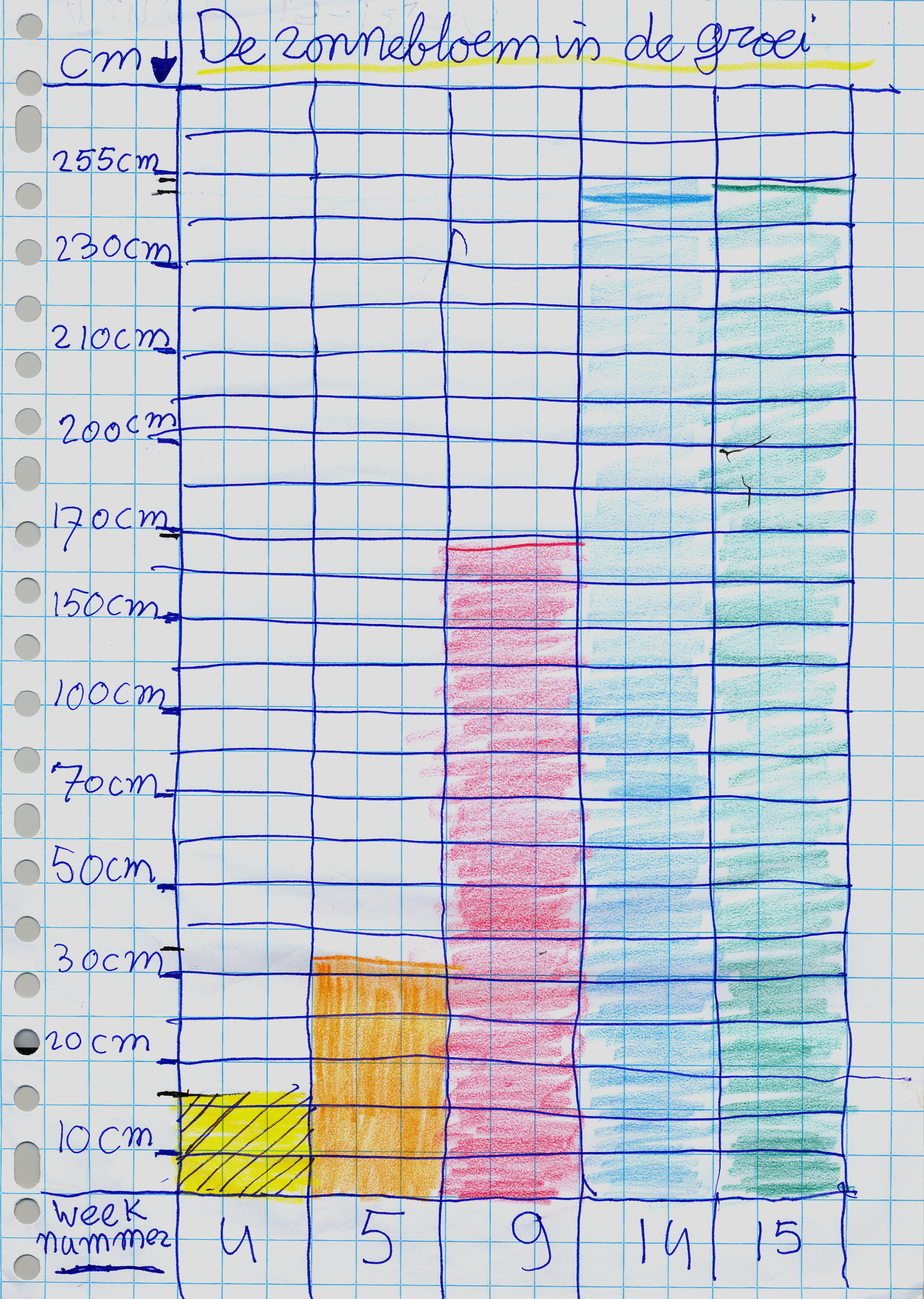
In order to make the step to a Cartesian graph, the need for proportionality of the axes of the student-made graphs has to be framed as a topic of discussion. The final sub-model may consist of graphs of continuous data. A rather obvious sub-model that may prepare for this is a segmented-line graph; a graph of discrete data in which the end points of the bars are connected by line segments, as shown in Figure 16.
Enlarge…
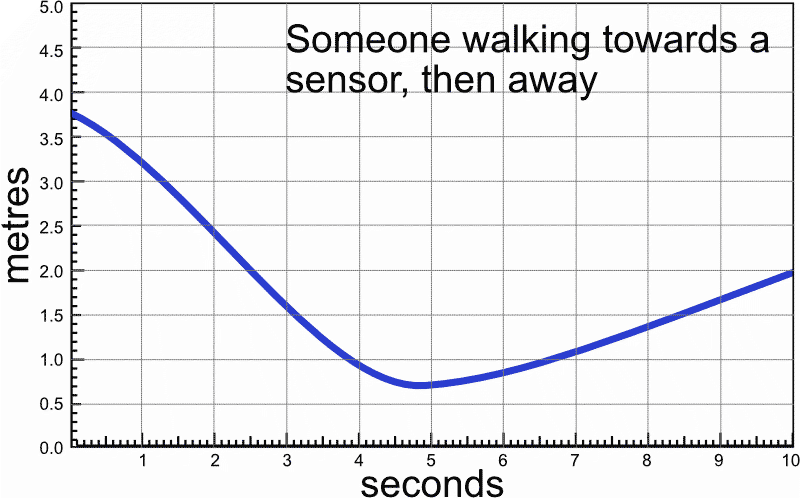
To foster the transition to graphs of continuous data, whole-class discussions may be focused on what points on those lines would signify, and how the steepness of the connecting lines could be interpreted. Here steepness has to be explicitly linked to the differences in the corresponding values on the horizontal axis and the vertical axis. Graphs of continuous data may be introduced as computer drawn graphs generated by a motion detector (see Figure 17), which become a topic of whole-class discussions (Van Galen, Gravemeijer, Van Mulken & Quant, 2012).
Enlarge…
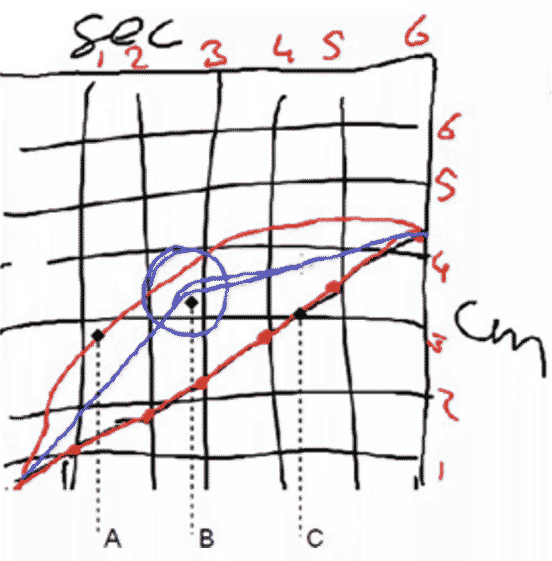
As an alternative, we may think of the context of filling glassware that was used by de Beer, Gravemeijer & Van Eijck (2018). Here the students themselves made the shape of the graph the topic of discussion. When the speed with which the water level in a cocktail glass would rise was visualized as a segmented-line graph of water height versus time, some students challenged the correctness of this graph. They argued that the rising speed was changing constantly, and that the graph therefore had to be curved (see Figure 18).
As summarized in Table 4, this analysis proposes the following series of sub-models:
- pictures or bars showing magnitudes, such as the heights of the sunflower at various points in time,
- bar graphs or case-point graphs with proportional axes,
- segmented-line graphs,
- curve.
|
Tool/inscription |
History/imagery |
Activity |
Mathematical issues |
|---|---|---|---|
|
Heights of plants |
Measuring heights of plants |
||
|
Series of pictures/case-value bars |
Heights of plants |
Describing the growth of plants visually |
Proportional representations |
|
Discrete proportional graphs |
Series of pictures/case-value bars |
Depicting measures proportionally |
Cartesian graphs |
|
Line graphs |
Proportional graphs of discrete data |
Interpolating Assessing growing speed |
Rise-over-run as a measure for rate of change |
|
Curve |
Line graphs |
Interpreting graphs of continuous data |
Graphs of continuous data |
5. Reflect on the sequence
Looking at the series of sub-models we may identify a shift from models of heights of sunflowers to models for reasoning about co-variation. Note that the first sub-model is static, the bars or pictures of sunflowers signify the lengths of a given sunflower at given moments in time. Later on, points on Cartesian plane are seen as showing how two variables co-vary. This coincides with a shift from measures as attributes to measures as potential values of a variable. In addition, we observe that the sequence involves graphs of empirical functions which may evolve into graphs that are defined algebraically later on. In this respect, the sequence on graphs not only serves as a prequel to a sequence on functions, but also overlaps to some extent with such a sequence.
Functions
We will continue with our last example, concerning a sequence on functions. Here we primarily draw on the so-called Tool Use project (Doorman, Drijvers, Gravemeijer, Boon, Reed, 2012) that was carried out in the Netherlands. The website “Functions and Arrow Chains” shows the introductory module based around the arrow applet.
1. Identify the instructional goals
An obvious starting point for a goal description is Sfard’s (1991) notion of the dual nature of functions as both processes and objects. The process aspect refers to calculating an output value for a given input value. The object aspect may be linked to the conception of a function as a set of ordered number pairs. Functions-as-objects can be seen as having certain characteristics—such as being linear, quadratic or periodic. Further, they can be subject to various operations, such as comparing, taking the inverse, and identifying families of functions. The object character also involves relations between three representations; algebraic expressions, tables and graphs (Janvier, 1987). Additional relations include the notion of a function as a dynamic process of co-variation; imaging an independent variable running through the domain set while the dependent variable co-varies (Drijvers, et al., 2007). Tables and graphs can be scrolled through or traced, and the character of the covariation can be related to the corresponding algebraic expressions. Note that each representation brings its own perspective on functions as objects. Graphs, for instance, instantiate the idea of a set of ordered number pairs, and illuminate characteristics such as being linear, quadratic or periodic. The algebraic aspect of a function as an object encompasses symbol sense and structure sense (Arcavi, 1994; Bokhove & Drijvers, 2010). This involves reading through algebraic expressions, realizing what symbols signify, breaking expressions into meaningful subexpressions, recognizing structure, and flexibly manipulating algebraic expressions, which may evolve into treating subexpressions as variables in and of themselves (Wenger, 1987)), and exploring the role of parameter. These may all be considered as belonging to a fully-fledged functions concept. For this exposition on emergent modeling, however, we will focus on the first phase, the shift from process to object.
2. Identify a central sub-model
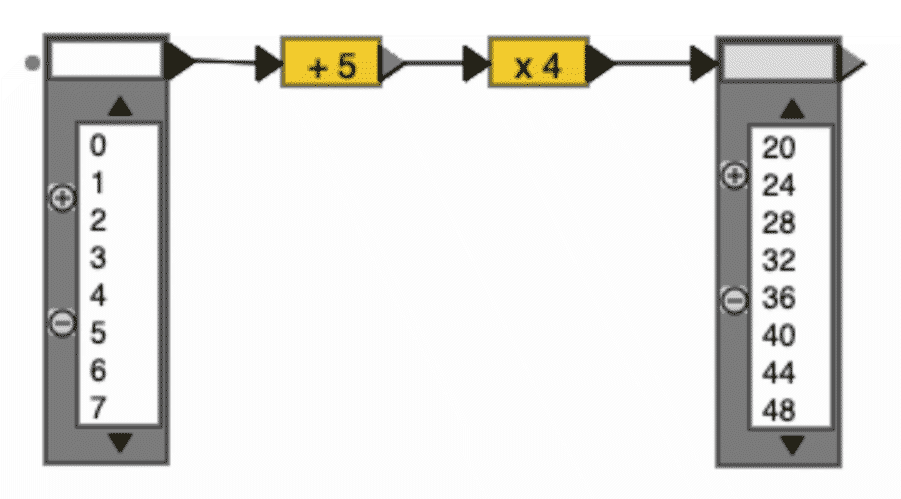
A common model to support instruction on functions is that of machines or arrows as shown in Figure 19, which takes any number, adds 3, squares the answer and then multiplies by 5.

Here, each machine or arrow represents one arithmetical operation. This model shows both the procedural, input-output, character of a calculational prescription, and the structure in terms of a sequence of operations. This may be exploited in two ways. One, by varying the input and applying the chain of operations on a set of input values creating a set of ordered number pairs. Second, by investigating how chains can be varied, curtailed and what an inverse chain would look like. Given those possibilities, the arrow chain is chosen as the central sub-model.
3. Identify instructional starting points
Starting points may obviously be chosen in contextual problems that involve the repeated executions of similar series of arithmetical operations. These may develop into recipes for generating the correct output for a given input. A potential starting point for middle-grade students might be the context of mobile-phone subscriptions, calculating the cost for various amounts of calling time (Drijvers, et al., 2007).
Enlarge…
4. Design a series of sub-models and identify the overarching model
Explicating how a series of sub-models might be developed, we will follow the approach of Drijvers et. al. (2007) in the Tool-use project. This project is especially interesting as it involved the development of a computer tool, named Arrow Applet (Boon & Drijvers, 2005). The computer tool enables students to design and use arrow chains for generating the output of a series of calculations for a variety of input values. It also offers the possibility of investigating the arrow chains themselves, for instance, by changing the order of the operations, curtailing or expanding arrow chains, or designing inverse arrow chains. The computer tool allows for generating tables of input and output values. Also, by enabling students to move up and down these tables, the computer tool supports the students in developing a dynamic notion of a function consisting of variables that can vary within spaces of possible values. Figure 20 shows a table generated for a function, which is described by the calculational prescription, ‘take a number, add 5, then multiply by 4’.
In terms of designing a series of sub-models, we argue that the series has to start with modeling the aforementioned contextual problems involving repeated executions of the arithmetical operations. Here the initial sub-model will obviously consist of number sentences and written text. Given our choice for the central sub-model, the number sentences will have to be replaced by arrow chains that signify the series of operations, as in Figure 19. Here students may first experiment with drawing arrow chains on paper, before getting introduced to the computer tool.
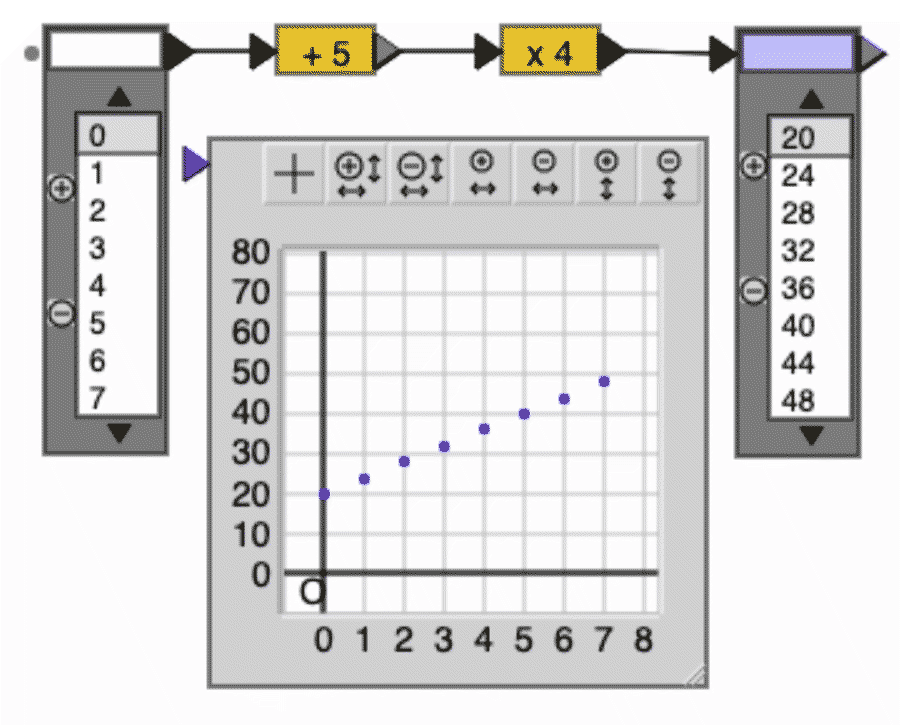
Enlarge…
To make the shift towards the structural conception of ordered number pairs, the model may be extended by adding the option to make tables, which we may consider the next sub-model. Apart from construing input-output tables as sets of ordered number pairs, the tables can also be investigated dynamically. As shown in Figure 20, the computer tool allows for having a variable running through the input or output column of the table to observe the co-variation.
To complete the integration of the three aspects of functions (expressions, tables and graphs), graphing has to be added in the next sub-tool. Figure 21 shows arrow chain, table and graph for the function ‘take a number, add 5 and multiply by 4’. We identify the arrow language as the overarching model.
5. Reflect on the sequence
The series of sub-models may be conceived as a transition from arrow language as a model of a fixed series of calculations to a model for reasoning about functions as objects. The series of sub-models making the chain-of-signification is summarized in Table 5.
|
Tool/inscription |
History/imagery |
Activity |
Mathematical issues |
|---|---|---|---|
|
Written calculation |
Finding output values |
Calculation recipe & notion of variable |
|
|
Machine/arrow language |
Written calculation |
Finding output values |
Calculation recipe & notion of variable |
|
Arrow chain in AA-applet |
Machine/arrow language |
Identifying input & output variables, and finding output values |
Calculation recipe & notion of variable |
|
Tables in AA-applet |
Arrow chain in AA-applet |
Investigating dependency |
Notion of variable, and relation between input and output variables |
|
Graphs in AA-applet |
Tables and arrow chains in AA-applet |
Investigating relations between functions |
Treating functions as objects (sets of ordered number pairs), characteristics of input-output relationships |
By generating arrow chains, tables, and graphs with the computer tool, students have the opportunity to treat functions as objects before they have become objects to them. We may observe, however, that further exploration is needed to develop a fully-fledged function concept. This may be achieved with additional Algebra Arrows applet option which allows inserting a letter into the input box. This results in an algebraic expression in the output box, as shown in Figure 22. The algebraic expressions are also shown. This opens up a variety of possibilities for exploring the relation between algebraic expressions, arrow chains and graphs.

Conclusion
The aim of this article is to lay out an operational version of the so-called emergent modeling design heuristic. We started by explaining and elaborating the heuristic with addition and subtraction up to 100 as an example. We showed that this heuristic originated within the context of a socio-constructivist elaboration of RME. Emergent modeling was operationalized by a series of guidelines, which encompass, (1) identifying the instructional goals; (2) identifying the central sub-model; (3) identifying instructional starting points; (4) designing a series of sub-models and identifying the overarching model; and (5)reflecting on the result. We discussed four examples to show how some existing designs could be reconstructed by using these guidelines; for these we identified goals in terms of mathematical objects and a network of mathematical relations:
- for addition and subtraction up to 20, developing and using a network of number relations,
- for introductory data analysis, construing the distribution of data in a data set as an object,
- for graphs, re-inventing graphing to make hidden conventions explicit
- for functions, conceptualizing functions as both procedures and objects.
We further showed that the central model may often be found by looking at the tactile and visual models that are already in use: ten-frames and the arithmetic rack for addition and subtraction up to 20; the dot plot for data analysis; the bar graph for graphing, and the arrow language for functions. To make such models fit the emergent modeling design heuristic, they have to be grounded in the experiential reality of the students. Thus, experientially real problem situations have to be sought that may be modeled with one of those models or a precursor thereof. Moreover, usually an in-between model is needed to make the transition from working with a model to more formal mathematical activity.
We argue that the above examples show the feasibility of the guidelines as heuristics for designing sequences—while acknowledging that there is always a creative act involved.
Acknowledgement
I would like to thank Frans van Galen for his comprehensive advice and technical support.
References
Arcavi, A. (1994). Symbol sense: Informal sense-making in formal mathematics. For the learning of mathematics, 14(3), 24-35.
Bakker, A. (2004). Design research in statistics education: On symbolizing and computer tools. (PhD Thesis). Utrecht, The Netherlands: CD-ß Press, Utrecht University. https://dspace.library.uu.nl/bitstream/handle/1874/893/full.pdf?sequence=2
Bereiter, C. (1985). Toward a solution of the learning paradox. Review of educational research, 55(2), 201-226.
Bokhove, C. & Drijvers, P. (2010). Symbol sense behavior in digital activities. For the learning of mathematics, 30(3), 43-49.
Beer, H. T. de, (2016). Exploring instantaneous speed in grade five: a design research. (PhD thesis). Eindhoven, The Netherlands: Eindhoven University of Technology. https://research.tue.nl/en/publications/exploring-instantaneous-speed-in-fifth-grade
Beer, H. T. de, Gravemeijer, K. P. E. & van Eijck, M. W. (2018). Exploring instantaneous speed in fifth grade.Educational Designer, 3(10), article 39. http://www.educationaldesigner.org/ed/volume3/issue10/article39/
Boon, P. & Drijvers, P. (2005). Chaining operations to get insight in expressions and functions. In Proceedings of the Fourth Congress of the European Society for Research in Mathematics Education (CERME 4), (pp. 969-978). Sant Feliu de Guíxols, Spain.
Buijs, K. (2008). Leren vermenigvuldigen met meercijferige getallen. (PhD Thesis). Utrecht, The Netherlands: Freudenthal Institute for Science and Mathematics Education.
Cobb, P., Boufi, A., McClain, K. & Whitenack, J. (1997). Reflective discourse and collective reflection. Journal for research in mathematics education, 28(3), 258-277.
Cobb, P., Gravemeijer, K., Yackel, E., McClain, K., and Whitenack, J. (1997). Mathematizing and Symbolizing: The Emergence of Chains of Signification in One First-Grade Classroom. In D. Kirschner, and J.A. Whitson (Eds.). Situated cognition theory: Social, semiotic, and neurological perspectives. (pp. 151-233). Hillsdale, NJ: Erlbaum.
Doorman, L. M. (2005). Modelling motion: from trace graphs to instantaneous change. (PhD Thesis). CD-β Press, Center for Science and Mathematics Education. https://dspace.library.uu.nl/handle/1874/1727
Doorman, M., Drijvers, P., Gravemeijer, K., Boon, P. & Reed, H. (2012). Tool use and the development of the function concept: from repeated calculations to functional thinking. International Journal of Science and Mathematics Education, 10(6), 1243-1267. DOI: 10.1007/s10763-012-9329-0
Drijvers, P., Doorman, M., Boon, P., Van Gisbergen, S. & Gravemeijer, K. (2007). Tool use in a technology-rich learning arrangement for the concept of function. In Proceedings of the V Congress of the European society for research in mathematics education CERME5. (pp. 1389-1398). Cyprus: Larnaca.
Fosnot, C.T. (2008). Bunk Beds and Apple Boxes: Early Number Sense. Heinemann.
Freudenthal, H. (1957). Report on a comparative study of methods of initiation into geometry, Euclides, 34, 289-306.
Freudenthal, H. (1973). Mathematics as an Educational Task. Dordrecht, the Netherlands: Reidel.
Freudenthal, H. (1983). Didactical phenomenology of mathematical structures. Dordrecht, the Netherlands: Reidel.
Freudenthal, H. (1991). Revisiting mathematics education: China lectures. Dordrecht, Netherlands: Kluwer.
Gravemeijer, K. & Cobb, P. (2013). Design research from the learning design perspective. In T. Plomp & N. Nieveen (Eds.) Educational design research. Part A: An introduction, (pp. 72-113). Enschede: SLO.
Gravemeijer, K. (1991). The empty number line as an alternative means of representation for addition and subtraction. Paper presented at the ICTMA 5 Conference, September 9 - 13, 1991, Noordwijkerhout, The Netherlands.
Gravemeijer, K. (1999). How emergent models may foster the constitution of formal mathematics. Mathematical thinking and learning, 1(2), 155-177.
Gravemeijer, K. (2020). A socio-constructivist elaboration of RME. In M. van den Heuvel-Panhuizen (Ed.) National Reflections on the Netherlands Didactics of Mathematics, Teaching and Learning in the Context of Realistic Mathematics Education, (pp. 217-233). Cham, Switzerland: Springer. https://link.springer.com/content/pdf/10.1007%2F978-3-030-33824-4_12.pdf
Gravemeijer, K., Bowers, J. & Stephan, M. (2003). Continuing the design research cycle: A revised measurement and arithmetic sequence. In Stephan, M., Bowers & J., Cobb, P., with Gravemeijer, K. (2003). Supporting students’ development of measuring conceptions: Analyzing students’ learning in social context. Journal for Research in Mathematics Education Monograph No. 12. (pp. 104-122). Reston, VA: National Council of Teachers of Mathematics.
Gravemeijer, K., Cobb, P. & Bowers, J. Whitenack. (2000). Symbolizing, Modeling and Instructional Design. In P. Cobb, E. Yackel & K. McClain (Eds.), Symbolizing and communicating in mathematics classrooms. Perspectives on discourse, tools, and instructional design. (pp. 225-273). Mahwah, New Jersey: Lawrence Erlbaum Associates.
Gravemeijer, K., McClain, K. & Stephan, M. (1998). Supporting students’ construction of increasingly sophisticated ways of reasoning through problem solving. In A. Olivier & K. Newstead (Eds.). Proceedings of the 22nd conference of the International Group for the Psychology of Mathematics Education, Volume 1, (pp. 1-194 - 1-209). Stellenbosch: PME.
Janvier, Claude (Ed.). (1987). Problems of representation in the teaching and learning of mathematics. Hillsdale, NJ: Erlbaum.
Jones, L. V. (1971). The nature of measurement. In R. Thorndike (Ed.), Educational measurement (2nd ed.), (pp. 335-355). Washington: American Council of Education.
La Bastide-van Gemert, S. (2015). All Positive Action Starts with Criticism: Hans Freudenthal and the Didactics of Mathematics. Springer Science+Business Media.
Larsen, S.P. (2013). A local instructional theory for the guided reinvention of the group and isomorphism concepts. Journal of Mathematical Behavior, 32(4), 712-725.
Latour, B. (1990). Drawing things together. In Lynch M and Woolgar S (Eds.), Representation in scientific practice. (pp. 19-68). Cambridge, MA: MIT Press.
Meira, L. (1995). The microevolution of mathematical representations in children's activity. Cognition and instruction, 13(2), 269-313.
Plaxco, D., Zandieh, M. & Wawro, M. (2018). Stretch directions and stretch factors: A sequence intended to support guided reinvention of eigenvector and eigenvalue. In S. Stewart, C. Andrews-Larson, A. Berman & M. Zandieh (Eds.), Challenges in Teaching Linear Algebra. (pp. 175-192), ICME-13 Monographs. Cham Switzerland: Springer.
Rasmussen, C. & Blumenfeld, H. (2007). Reinventing solutions to systems of linear differential equations: A case of emergent models involving analytic expressions. The Journal of Mathematical Behavior, 26(3), 195-210.
Rasmussen, C., Dunmyre, J., Fortune, N. & Keene, K. (2019). Modeling as a means to develop new ideas: The case of reinventing a bifurcation diagram. PRIMUS, 29(6), 509-526.
Sfard, A. (1991). On the dual nature of mathematical conceptions: Reflections on processes and objects as different sides of the same coin. Educational studies in mathematics, 22(1), 1-36.
Stephan, M. & Akyuz, D. (2012). A proposed instructional theory for integer addition and subtraction. Journal for research in mathematics education, 43(4), 428-464.
Stephan, M., Bowers, J. & Cobb, P., with Gravemeijer, K. (2003). Supporting students’ development of measuring conceptions: Analyzing students’ learning in social context. Journal for Research in Mathematics Education Monograph No. 12. Reston, VA: National Council of Teachers of Mathematics.
Streefland, L. (1985). Wiskunde als activiteit en de realiteit als bron, Nieuwe Wiskrant 5(1), 60-67.
Treffers, A. (1987). Three Dimensions. A model of goal and theory description in mathematics education: The Wiskobas Project. Dordrecht: Reidel.
Treffers, A. (1991a). Didactical background of a mathematics program for primary education. In L. Streefland (Ed.), Realistic mathematics education in primary school. (pp. 21-56). Utrecht, The Netherlands: Freudenthal Institute, Utrecht University.
Treffers, A., (1991b). Het rekenrek 1&2. Willem Bartjens, 8(3-4), 151-153.
Van Den Heuvel-Panhuizen, M. (2003). The didactical use of models in realistic mathematics education: An example from a longitudinal trajectory on percentage. Educational studies in Mathematics, 54(1), 9-35.
Van den Heuvel-Panhuizen, M. & Drijvers, P. (2014). Realistic mathematics education. Encyclopedia of mathematics education, 521-525.
Van Eerde, H. A. A. (1996). Kwantiwijzer. Diagnostiek in reken-wiskundeonderwijs. Tilburg, Netherlands: Zwijsen.
Van Galen, F. & Gravemeijer, K. (2010). Dynamische grafieken op de basisschool. Utrecht, Netherlands: Freudenthal Instituut.
Van Galen, F. & Markusse. A. (2018). Inzicht ontwikkelen: Een pleidooi voor geleid heruitvinden. Volgens Bartjens, 37(5), 4-8.
Van Galen, F., Gravemeijer, K., Van Mulken, F. & Quant, E. (2012). Kinderen onderzoeken ‘snelheid’. Eindhoven, Netherlands: Eindhoven School of Education.
Van Hiele, P. V. (1973). Begrip en inzicht. Purmerend, the Netherlands: Muusses.
Walkerdine, V. (1988). The mastery of reason. London: Routledge.
Wawro, M., Rasmussen, C., Zandieh, M., Sweeney, G. F. & Larson, C. (2012). An inquiry-oriented approach to span and linear independence: The case of the magic carpet ride sequence. Primus, 22(8), 577-599.
Wenger R.H. (1987). Cognitive science and algebra learning. In A. Schoenfeld (Ed.), Cognitive science and mathematical education. (pp.217 – 251). Hillsdale, NJ: Lawrence Erlbaum Associates.
Whitney, H. (1988). Mathematical reasoning, early grades. Princeton (Unpublished paper).
Yackel, E. & Cobb, P. (1996). Sociomathematical norms, argumentation, and autonomy in mathematics. Journal for research in mathematics education, 27(4), 458-477.
Zandieh, M. & Rasmussen, C. (2010). Defining as a mathematical activity: A framework for characterizing progress from informal to more formal ways of reasoning. The journal of mathematical behavior, 29(2), 57-75.
Appendix
Design experiments using the emergent modeling design heuristic
|
Addition and subtraction up to 20 |
Gravemeijer, Cobb, Bowers & Whitenack (2000) |
|
Addition and subtraction up to 100 |
Stephan, Bowers & Cobb with Gravemeijer (2003) |
|
Two-digit multiplication |
Buijs (2008) |
|
Column algorithms for addition and subtraction |
Gravemeijer, McClain & Stephan (1998) |
|
Integer addition and subtraction |
Stephan & Akyuz (2012) |
|
Introductory data analysis |
Gravemeijer & Cobb (2013) |
|
Introductory data analysis |
Bakker (2004) |
|
Graphing |
Van Galen & Gravemeijer (2010) |
|
Functions |
Drijvers, Doorman, Boon, Van Gisbergen & Gravemeijer (2007) |
|
Calculus |
Doorman (2005) |
|
Instantaneous speed |
De Beer (2016) |
|
Differential equations |
Rasmussen & Blumenfeld (2007) |
|
Bifurcation diagram |
Rasmussen, Dunmyre, Fortune & Keene (2019) |
|
Introductory linear algebra |
Wawro, Rasmussen, Zandieh, Sweeney & Larson, (2012) |
|
Matrices |
Andrews-Larson, Wawro & Zandieh (2017) |
|
Non-Euclidean geometry, triangles on a sphere |
Zandieh & Rasmussen (2010) |
|
Group and isomorphism concepts |
Larsen (2013) |
|
Eigenvectors & eigenvalues |
Plaxco, Zandieh & Wawro (2018) |