e-Proofs: Design of a Resource to Support Proof Comprehension in Mathematics
Lara Alcock & Nicola Wilkinson
The University of Loughborough
Abstract
1
This paper presents a theoretical basis for the design of e-Proofs,
electronic resources to support proof comprehension in undergraduate
mathematics. To begin, we frame the problems of teaching for proof
comprehension, giving research background and an argument about what
teacher-centred lecturing does not, and cannot, do to address these. We
then describe e-Proofs, discuss the way in which they have been used in
an Analysis course, and review their limitations and affordances as part
of an overall educational experience. Finally, we briefly describe the
development of a web-based tool for constructing e-Proofs, ways in which
this tool will be used to different pedagogical ends, and associated
research activity.
Introduction
2
Proofs in undergraduate mathematics
In many undergraduate mathematics lectures, the lecturer spends a
large proportion of the time presenting proofs of theorems (Weber,
2004). Much of the prose in textbooks also consists of proofs (Raman,
2004), and there is a clear assumption that students will learn a great
deal of mathematics by reading the proofs of others (Selden &
Selden, 1995). This paper is about what this entails and the design of
an electronic resource to support it. This introduction presents an
example of the type of proof students encounter and gives some first
observations about its structure and about the thinking required to
understand it.
Students in a proof-based lecture course would typically be
presented with proofs like that for Rolle’s Theorem as shown in Figure 1. Most first courses in Analysis would include
this theorem and a version of the proof, which is not atypical of proofs
at this level; some would be shorter but some would be longer and more
complicated, and such a course might involve around 20 such proofs.
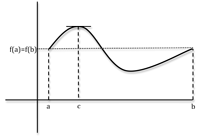
Students might also be shown an accompanying diagram; one for Rolle’s
Theorem is shown in Figure 2.
For many people the diagram will confirm intuitively that the
theorem is correct. The proof is nonetheless provided, with the
expectation that the student will attempt to understand it. This
expectation is probably different from earlier mathematics courses in
which the student may have been asked to study and apply theorems (eg. (Hughes-Hallett, Gleason et. al. [1994] introduce the Mean Value
Theorem without proof and use it in exercises on Taylor polynomial
approximations). It is, however, consistent with the aim that students
should come to understand mathematical theories as systems of
interconnected results, all proved on the basis of agreed definitions
and forms of reasoning (cf. Bell, 1976; de Villiers, 1990).
Understanding a proof: Some first observations
This proof is typical in that both the theorem and the proof are
written using a combination of words and algebraic notation, the latter
of which can be read out loud so that the whole proof consists of
well-formed English sentences. Clearly, a student will need to be
familiar with the names and meanings all of these words and symbols in
order to read the proof fluently and understand it (notation used is
summarised in Appendix
A).
The proof is structured so that it begins with the assumptions
from the theorem premises and ends with the conclusion. The first three
lines prove that there exists a point x1 at which f has a minimum
on the interval – all function values on the interval are greater than or
equal to f(x1) – and a point at which it has a maximum. The remaining lines
rely on this information, and collectively form a subproof by cases
that, whether or not this maximum and minimum occur at the endpoints,
there is necessarily a point at which the derivative of the function is
zero. For a full understanding, the reader will need to recognise this
structure.
The proof explicitly quotes two other theorems, the Extreme Value
Theorem and the Interior Extremum Theorem, both of which would probably
have been proved earlier in the same course and are used without being
written out. The proof also uses various defined concepts. Again, these
definitions are not written out in the proof, and unlike the theorems,
they are not explicitly invoked. Indeed, some (maximum and minimum) are
used directly, but some (continuity and differentiability) are built
into the assumptions of the quoted theorems. For a full understanding,
the reader will therefore need to recall these definitions and theorems
and examine the ways in which they are being used (all of these
definitions and theorems are listed in Appendix A).
Clearly it is not a trivial exercise to identify this structure
or to recall and examine the relevant information. In the next section,
we give a more detailed theoretical breakdown of the skills this
requires and describe research indicating the degree to which we can
expect students at the undergraduate level to have these skills.
Theoretical issues: Framing the problem
3
Literature on students and proof
The literature on students’ experience of mathematical proof has
documented difficulties in constructing proofs (eg., Harel & Sowder,
1998; Moore, 1994; Weber, 2001) and in validating proofs or assessing
whether types of argument are acceptable (eg. Healy & Hoyles, 2000; Knuth, 2002; Raman, 2003; Recio & Godino, 2001; Segal, 2000; Selden
& Selden, 2003). This work is relevant to proof comprehension as
discussed below, although various authors have noted that the issue of reading proofs has received comparatively little research attention (Hazzan
& Zazkis, 2003; Mamona-Downs & Downs, 2005; Selden & Selden,
2003).
Approaches to proof comprehension
Not everyone goes about proof comprehension in the same way, and
one approach is to examine how the statements and arguments relate to
particular examples or diagrams. Weber (2008), for instance, documented
cases in which mathematicians used examples while validating proofs, and Movshovitz-Hadar and Hazzan (2004) reported on a lecturer who used an
extended example to motivate and explain a theorem and proof in group
theory. Such a tactic might be called a semantic approach, by analogy
with semantic proof construction strategies described in Weber and
Alcock (2004) and Alcock and Inglis (2008). e-Proofs, however, focus on
supporting comprehension by explicating the relationships among the
theorem premises and conclusions, the individual lines of the proof, and
external information such as established definitions and theorems. This
might be considered a syntactic approach, again by analogy with a proof
construction strategy in which the reasoner proceeds “by moving between
agreed configurations such as definitions and theorems statements by
applying the rules of logic, standard proof frameworks and so on”
(Alcock & Inglis, ibid. p.115).
In the next sections we give a theoretical breakdown of a
syntactic approach to proof comprehension, organising this discussion
around Lin and Yang’s characterisation of facets of proof comprehension.
Lin and Yang identified these facets on the basis of existing literature
and interviews with mathematicians and mathematics teachers (Yang &
Lin, 2008). They used them to design proof comprehension questions for a
purportedly student-produced proof in geometry, and used the resulting
test as part of an empirical study (Lin & Yang, 2007). For each
facet we do the following: 1) describe its meaning and its
operationalisation via comprehension test questions; 2) compare with
observations about the Rolle’s Theorem proof from the introduction and
with proof comprehension questions from Conradie and Frith (2000) based
on a standard proof that is irrational (reproduced in the Appendix B);
and 3) discuss what other research literature tells us about relevant
student competencies.
Basic knowledge
Lin and Yang’s first facet is called basic knowledge,
which they operationalised as recognising the meaning of a
symbols in a figure and explaining/recognising the meaning of a
property (Lin & Yang, 2007 p.750). They tested basic knowledge via
questions that asked for labelling figures, comparing angles etc. Conradie and Frith (2000, p.227) included comparable questions on
background conceptual or procedural knowledge, for instance requesting
definitions:
As noted in the introduction, basic knowledge of definitions and
earlier theorems would also be necessary to understand the proof of
Rolle’s Theorem. In addition, students some way into an undergraduate
degree would be expected to be fluent in various forms of algebraic
manipulation, to be able to state the meaning of symbols like “∃” and to
be able to correctly interpret sentences containing these.
Unfortunately, we cannot expect that students will necessarily
have the required background knowledge. New definitions and theorems
appear on a daily basis in undergraduate courses, and it is unrealistic
to think that students will have all of these at their fingertips. Also,
research indicates that undergraduates are often inaccurate in
interpreting the logic of mathematical statements involving conditionals
and quantifiers (Dubinsky & Yiparaki, 2000; Epp, 2003; Hazzan &
Leron, 1996; Selden & Selden, 1995). Further, students often do not
attend to definitions, instead relying on concept images (Vinner, 1991),
even when working with concepts for which they have minimal prior
experience (Edwards & Ward, 2004). This is important because of the
way in which precise statements of definitions are used in proofs. For
instance, in the Rolle’s Theorem proof, the formal definitions of
minimum and maximum are combined and used to formulate line 3; a student
who has only an intuitive idea that the maximum occurs “where the
function is biggest” is not likely to recognise this. Of course, seeing
mathematical language and definitions used in proofs is one way in which
students learn about them, but inexperience will impede comprehension of
any given proof in the meantime.
Logical status (inferring warrants)
Lin and Yang’s second facet is called logical status,
which they operationalised as recognising a condition applied
directly, judging the logical order of statements and recognising
which properties are applied (Lin & Yang, 2007 p. 351). They tested
this via questions about possible reordering of lines and about which
properties are used at different stages. Conradie and Frith (2000,
p.227) included questions with similar aims, for example:
Such questions require two things. First, the reader needs to
shift their focus from the content of each statement to its status; to
see statements in the proof as premises and conclusions, and indeed to
be able to treat the same statement as conclusion at one stage and
premise at the next (Duval, 2007). Second, the reader must infer
the warrant that the proof’s author is using in order to justify the new
statement. We use this term in the sense of Weber and Alcock (2005), who
use a restricted version of Toulmin’s (1958) scheme in which an argument
is seen as composed of data, warrant and conclusion. For instance, in
the second of Conradie and Frith’s questions, the data is that 5 is a
factor of m2 and the conclusion is that 5 is a
factor of m. Both of these appear in the proof. The question
asks the reader to infer the warrant, which does not. Weber and Alcock
point out that this is common: readers often have to infer warrants
because these are often implicit in textbook proofs. In fact, when
inferring warrants, the focus might need to be broadened to other lines
of the proof, because it is common for the data to be distributed across
the preceding lines and the theorem premises. For instance, in the
Rolle’s Theorem proof, use of the Interior Extremum Theorem requires the
function to have a maximum or minimum on the interior of an interval, as
assumed in line 7, and requires the function to be differentiable on
that interval, as assumed in line 1.
Again, it is not realistic to assume that students will be able
to do all of this easily. First, students will be accustomed to everyday
argumentation in which the focus is on the content of the statements
rather than on their status within a larger structure (Duval, 2007).
Second, a student who does not accurately interpret conditional and
quantified mathematical statements is unlikely to infer warrants
appropriately, and a student who is not conversant with earlier
definitions and theorems will be further hampered in this process.
Third, and more importantly, research on proof validation indicates that
students may not even attempt to infer warrants when reading
proofs. Selden & Selden (2003), for instance, found that students
who were asked to check the validity of short number theory proofs often
did not notice when one line did not follow from the line above.
Similarly, Alcock and Weber (2005) found that only two out of 13
undergraduate students correctly inferred and rejected a fairly
straightforward invalid warrant in an Analysis proof. Weber (2009) found
that 28 undergraduates who had completed a transition-to-proof course
rarely spent more than two minutes deciding whether purported proofs
were valid. They were often prepared to make a validity judgment despite
acknowledging their own incomplete understanding; at least some appeared
to believe it to be the responsibility of the proof’s author to spell
out all the details, so that the fault in understanding in these cases
lay with the author and not with the reader. This indicates that a
substantial number of students may not read proofs in a way that is
likely to lead to understanding of their logic.
Summarisation (identifying larger scale structure)
Lin and Yang’s third facet is summary, which they
operationalised as identifying critical procedures, premises or conclusions and indentifying critical ideas of a
proof (Lin & Yang, 2007, p.751). They tested this via questions
about what the proof shows and about identifying a significant
intermediate result and how it is used. Conradie and Frith (2000,
p.227-228) again included questions with similar aims, such as:
-
What method of proof is used here?
-
Which assumption is contradicted, and how does the theorem
follow from this?
The introduction to this paper discussed such overall structure
for the proof of Rolle’s Theorem. Duval (2007, p.142) captured another
such structure with the aid of a tree diagram for a geometry proof in
which the theorem premises are used to prove two independent
intermediate results, which are then put together to arrive at the
required conclusion.
Identifying such structure requires understanding the proof at a
more global level, looking for major steps, subproofs and standard
structures within these subproofs or the proof as a whole. Again,
accurate interpretation of conditional and quantified statements will be
required to do this fully. Knowledge of definitions will be highly
relevant because statements like “Prove that x is an X”
need to be interpreted as “Prove that x satisfies the
definition of X”(cf. Alcock and Simpson, 2002), meaning that
definitions often form structures for proofs. Selden and Selden (2003) discussed this point in detail, arguing that definitions and other
statements often dictate the top-level structure of a proof. Difficulty
in identifying larger-scale structures is likely to be exacerbated by
confusion over particular argument structures such as proof by induction
(eg., Dubinsky, 1987; Harel, 2001) or contradiction (eg., Antonini &
Mariotti, 2008).
Generality
Lin and Yang’s fourth facet is generality, which they
operationalised as justifying correctness and identifying
what is validated by the proof (Lin & Yang, 2007, p.751). They tested this via
questions that asked whether the purported proof was valid and whether
it proved that the target statement was sometimes or always correct.
Conradie and Frith included a question in which a proof appeared without
its corresponding theorem and the student was asked what had been proved
(Conradie & Frith, 2000, p.228).
Questions of this type might seem irrelevant to a lecture in
which a correct theorem and proof is presented, so that there is no
question of validity or scope. However, we would still want the student
to understand that the proof does in fact prove the specified statement,
and this might be problematic. Selden and Selden (2003) found that in
validating short purported number theory proofs, only two out of eight
students initially spotted that one of these was a proof of the converse
of the target theorem (also incorporating a notational error). Weber
(2009) reported similar results. It is worth noting that in these
studies, along with that of Alcock and Weber (2005), many of the
arguments used were only four lines long. This is substantially less
than the length of many proofs presented in undergraduate lectures.
Combining skills
Describing these facets in this order emphasizes that some are
more local (understanding particular lines) and others more global
(understanding overall structures). This should not be taken to mean
that one proceeds in understanding a proof in this order. Weber (2008),
for instance, found that mathematicians faced with proofs in an
unfamiliar area typically began by identifying the global structure and
then proceeded to a line-by-line check. Clearly, however, developing a
full understanding of a proof is a complicated process, and there is a
lot of scope for proofs to be poorly understood.
Practical issues: The problem of lecturing
4
Research-based responses to difficulties with proof
In recognition of students’ difficulties, mathematics educators
have suggested various ways of making proofs more accessible. Rowland
(2001), for instance, suggested that proofs using a generic example
might be more comprehensible than fully general proofs. Harel (2001) described an approach to proof by induction that begins with repeated
experience of constructing recursion arguments. Leron (1985), described
both an approach to contradiction that involves working first on the
central constructive idea, and a general approach in which a proof task
is broken into chunks to highlight its overall structure (Leron, 1983).
Others have focused on student-centered reform-oriented instruction in
which entire courses have been redesigned in order to give students more
responsibility for constructing proofs (eg., Alcock & Simpson, 2001; Rasmussen and Marrongelle, 2006; Zandieh, Larsen and Nunley, 2008).
However, neither type of research has not had a strong influence
on how proofs are presented. In the latter case this is partly because
of resource issues: many lecture classes involve well over 100 students,
a situation that does not lend itself to involving the students as a
coherent knowledge-building community and that is not going to change
any time soon. While large lectures do not have to be run entirely on a
transmissionist model (eg., Biggs & Tang, 2007), lecturer-provided
explanations are likely to remain a mainstay of the undergraduate
mathematical experience for the foreseeable future.
Explanations in lectures
In presenting a proof, a lecturer typically writes it on the
board one line at a time, giving additional explanation about why each
line is valid. He or she might also give an overview of the argument,
state rationales for certain approaches, point out sections that achieve
different subgoals, and relate these to the overall structure of the
theorem (eg., Movshovitz-Hadar & Hazzan, 2004; Weber, 2004).
These explanations may be clear and informative, but there are
several problems with expecting them to lead to proof comprehension.
First, they require the student to draw on background knowledge,
recognise and validate cited warrants, and recognise larger scale
structures and generality, all in rapid succession. Second, although the
lecturer will try to facilitate this process with reminders, hand
gestures and so on, the student’s attention may not be directed
precisely enough. Third, even if a student’s attention is in the right
place(s), they may not be able to grasp the logical relationships
quickly enough to understand them, especially if this involves recalling
an earlier theorem or results from earlier lines. Fourth, each student
is likely to have slightly different difficulties in following the
explanation, and the lecturer cannot take a few minutes to pause for
each of these. Fifth, whatever explanation is offered is ephemeral and
is typically no longer available when the student comes to re-read their
lecture notes. This means that even a dedicated student who pays
attention in lectures must reconstruct it during independent study.
Once these problems are recognized, one practical solution would
be to record the lecture. This would allow a student to see and hear
explanations again, but does not address the problems of directing
attention precisely or of seeing relationships in real time. Also, there
may be slips and hesitations in the spoken explanation, visuals and
audio are unlikely to be optimally clear, and there may be extraneous
distracters in either. Another solution would be to provide additional
written information to accompany the proof. This is sometimes done,
perhaps in a two-column format as by the professor studied by Weber
(2004). However, giving more detail might obscure the structure of the
proof, as other authors have noted: “to make a proof too detailed would
be more damaging to its readability than to make it too brief” (Davis
& Hersh, 1985, p.73) and “[the student may] have difficulty
distinguishing supplementary and explanatory remarks from the proof
itself” (Selden and Selden, 1995, p. 140). Annotations and further
explanation might well be useful, but we suggest that adding these as
additional text is not an optimal delivery method, and that a
technological solution can do better.
e-Proofs
5
Initial design
e-Proofs are designed to address theoretical proof comprehension
issues within the practical context of traditional lectures, by making
the structure and reasoning used in a proof more explicit without
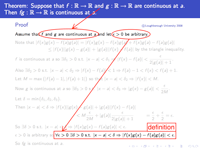
cluttering its presentation. Each e-Proof consists of a sequence of
screens such as that shown in Figure 3. Each screen shows the theorem
and the whole proof, with much of the latter “greyed out” to focus
attention on particular lines. Relationships are highlighted using boxes
and arrows, and each screen is accompanied by an audio file which
students can listen to as many times as they wish.
The screen in Figure 3 comes from what we have termed the line-by-line version of this e-Proof. We also constructed chunk versions, the
aim of which is to focus attention on the global structure of the proof
by breaking it into relatively self-contained sections or subproofs. Figure 4 shows a screen from the chunk version of the same e-Proof.
Improvements in a new version
The e-Proof screens shown above were constructed by using Beamer
to convert a LaTeX file into a pdf presentation, which was then
annotated and separated into screens. The audio was recorded using
Audacity. This content was then uploaded to the university’s virtual
learning environment (VLE), making use of one of its standard lesson
structures. This was a somewhat clumsy process involving uploading
screens and audio separately, and was restricted by the content and
structure of the rest of the VLE’s standard layout.
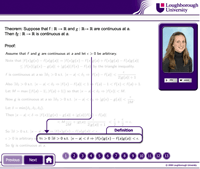
Figure 5 shows a prototype improved version made using Flash. In
this version, annotations are better synchronized with the audio
content, so that the arrows and boxes appear and disappear exactly when
they are needed. (If you are reading this article online, you can run the complete e-Proof).
Addressing theoretical and practical issues
In the theoretical framework section we discussed four facets from Lin and Yang’s (2007) breakdown of proof comprehension: basic knowledge
(relevant background procedural and conceptual knowledge), logical
status (inferring warrants), summary (identifying critical ideas and
subproofs) and generality (identifying what is proved). Each of these
can be supported by e-Proofs.
Basic knowledge can be supported in a low-level way simply by
providing correct and fluent reading of all of the words and symbols in
the proof. Indeed, such reading might highlight important conceptual
information, if for example a statement like “|x - a| < δ” is read out loud as “the
distance between x and a is less than delta”. Basic
knowledge can also be supported by providing audio reminders of relevant
definition and theorem statements. Reading for logical status can be
supported by giving explicit audio explanations of implicit warrants.
Annotations can highlight which information is being used as data for a
particular claim, even when this is dispersed across the proof, and can
visually link this information to the conclusion. Reading in order to
identify critical ideas and subproofs can be supported either by
indicating their beginnings, ends and internal structure with
line-by-line annotations or by breaking proofs down as in the chunk
version and providing commentary on what is achieved in each section.
Finally, reading in order to identify what is proved can be supported by
providing a screen with arrows indicating where the theorem premises are
used and where the conclusion appears.
All of this information could be provided in a lecture, but here
the explanation is not only captured but enhanced by directing attention
precisely and having clear visuals and audio. Low-level details are
hidden but retrievable, navigation to a specific point of difficulty is
straightforward, the audio can be replayed as many times as the student
wishes and the reader can proceed at his or her own pace. Also, the
annotations appear one at a time and do not permanently add content, so
the integrity of the proof is preserved without clutter. Overall, the
coordination of the static underlying proof and the dynamic annotations
and audio mean that the thinking one needs to do to understand a proof
is made explicit in a way that could not be achieved in a lecture or a
book.
Design, implementation and usage
6
Design of individual e-Proofs
Designing an e-Proof requires considerable intellectual work
because of two coordinated constraints: the screen size and the length
of each audio explanation. Making a proof fit on one screen often
requires compression compared with what might be written on a board.
Such compression is possible because some of the explanation that might
ordinarily appear in a board version can be put in the audio commentary
(“by line 3”, “this contradicts our assumption at *”, and so on). On the
other hand, the logic of the written version needs to remain clear, and
the audio itself is also constrained. Laurillard (2002, p.110) states:
“If a hyperlinked clip lasts longer than thirty seconds there is a sense
of the user having ceded control, and they revert to being the viewer,
rather than active participant…. Ten to twenty seconds is more
comfortable.” Coordinating these aspects, however, is easier than
deciding on the content of the explanation and how this will relate to
what is fully visible on the screen and what annotations should appear.
The difficulty of constructing satisfactorily short, fixed explanations
further convinced us of the likely inadequacy of the on-the-fly
explanations typically given in lectures.
Implementation
The first author constructed eight e-Proofs for an Analysis
course that covered
standard content on continuity, differentiability and Riemann
integrability and was given to a cohort of 140 students in Autumn, 2008.
For each e-Proof she first gave out printed copies of the theorem and
proof and invited the students to spend a few minutes reading and
discussing these. She then showed the line-by-line and chunk versions of
the e-Proof, playing most of the audio but sometimes inviting the
students to confirm that they could see how a simple line worked without
it. If appropriate, she also drew a diagram on the board as the proof
progressed. This whole process typically took approximately 15-25
minutes, and the students did not receive any particular instruction on
what they should do while the e-Proof was shown. Subsequently she saw a
number of printed copies with copious annotations, but does not know
whether these were made during lecture time. After the lecture, the
e-Proof was made available via the course VLE page.
This experience of using the e-Proofs led her to two main
observations. First, when the first e-Proof was shown, the students
seemed somewhat daunted. We believe this indicates that the e-Proof made
clear how much work that might go into understanding a proof. Second,
the use of e-Proofs had a noticeable effect upon her lecturing, in that
she made many more comments than usual about the process of
understanding proofs. She commented on what to look for in seeking
line-by-line links and overall structure, related this to the experience
of watching e-Proofs and indicated that this is something a student
should do for every proof. In doing so she stressed that this process
should take some time, but not an impossible amount. Using e-Proofs thus
made the process of proof comprehension an overt subject of discussion
in the lectures.
Usage
The VLE collects usage data for all the posted documents and
other types of activity, so it is possible to ascertain how much the
e-Proofs were actually used by the students. The e-Proofs were
collectively viewed a total of 1026 times during the course and in the
pre-examination period (seven viewings per student on average), with
more viewings in this latter period. This was comparable with usage of
other online resources such as solutions to not-for-credit weekly
problem sheets. Feedback was positive, with the vast majority of
students indicating that they would like e-Proofs for other courses. For
more detail on usage and feedback see Alcock (2009).
Discussion: Pedagogical affordances and limitations
7
What e-Proofs do not do
e-Proofs were designed to address the problem of teaching for
proof comprehension in large, teacher-centred undergraduate mathematics
lectures. We have argued that in theory, they can focus attention on the
thinking needed for syntactic proof comprehension by making explicit
both warrants for line-by-line validity and larger-scale structure.
However, it is important to recognize the limits on what such a resource
can contribute to the overall learning process (the following is much
influenced by Laurillard, 2002).
Essentially, an e-Proof allows the lecturer to articulate their
own understanding of a proof. We have argued that it allows them to do
this better than they could in a lecture or a standard written
explanation, but it is still just an explanation. The lecturer can
attempt to anticipate likely points of difficulty, but students have no
opportunity to articulate their own conceptions and receive feedback on
these. In this respect, e-Proofs are considerably less sophisticated
than what Laurillard (2002, chapter 7) calls adaptive media. In
mathematics education, one might see this by comparing with CAA (see eg. Sangwin, 2004), which can provide extrinsic feedback by responding to
anticipated answers in particular ways, and with dynamic geometry
software (see eg., Hadas, Hershkowitz & Schwarz, 2000), which can
provide intrinsic feedback by allowing the student to immediately see
the effect of their constructions and dragging actions.
e-Proofs are interactive, but only in the weak sense
that the student controls the pace and sequence of the content and can
replay parts at will. In discussing interactive media, Laurillard (2002,
p.110) notes that “[w]ithout a clear personal goal, students will tend
to iterate through the resource without either reflection or
adaptation”. In this case, a student can sit in front of an e-Proof
without thoughtfully engaging just as easily as they can sit in a
lecture without thoughtfully engaging. In the Analysis course, e-Proofs
were combined with other types of instruction and activity, some of
which encouraged students to share their understanding with each other
and then reflect upon it when the e-Proof was played or a solution was
made available. As in any learning situation, consideration must be
given to the student’s perception of what they are supposed to be
learning and how the learning activities and resources are supposed to
support that (see eg., Ramsden, 2003).
Continuing work
8
Research and teaching
e-Proofs are designed to support proof comprehension, and with
the support of an MSOR Network mini-project award, a research study has been
undertaken to investigate whether they actually do. This project
compared students’ comprehension of a proof after a) studying an
e-Proof; b) watching a lecture; and c) reading the proof independently.
Roy, Alcock & Inglis (2010) report that in this first exposure to a
particular proof, the lecture led to the greatest comprehension. They
discuss possible reasons for this, which are closely related to the
limitations of e-Proofs as discussed above. This work links to the work
being carried out by the ExPOUND Project (see below), where we will be
documenting how and why students use e-Proofs, both in terms of their
detailed interaction with particular proofs and as part of their overall
study for a course. Finally, lecturers at Loughborough will be exploring
the possibility of allowing students to construct their own e-Proofs for
submission as part of an assignment in a course on Communicating
Mathematics. In this way it is hoped that e-Proofs will allow students
not just to better understand lectured proofs, but to demonstrate their
own understanding of proofs that they have studied from other sources.
ExPOUND project
With the support of a JISC Learning and Teaching Innovation Grant, work is
now underway to develop an open-source web-based tool called ExPOUND
(Explaining Proofs: Offering Understanding through Notated
Demonstrations). The tool has been designed to allow both lecturers and
students to construct e-Proofs as illustrated in the improved prototype
version as shown in Figure 5. The tool itself is written in Flex and
PHP, using both rapid prototyping and agile development practices, and
has been released under an open source license so that it can be
installed for use at other institutions and the underlying code can be
modified for bespoke functionality. The individual ExPOUND user will,
however, be able to construct an e-Proof through a web browser so no
installation will be required. The user will be able to share their
project build files so that others can make modifications for their own
settings, and the finalised e-Proofs will be a Flash files, allowing
easy sharing of these learning objects via, for example, an
institutional VLE.
The ExPOUND team has gathered early feedback by meeting with
lecturers interested in being able to use both the ExPOUND tool and the
e-Proof products in their teaching practice. Early indications have been
positive: the lecturers engaged with the team, noted potential
limitations and suggested additional features that would be useful to
them. Many of these suggestions have been incorporated into the initial
tool and/or documentation. Early interest has been from mathematicians,
but lecturers from other disciplines such as design and technology and
chemical engineering are also beginning to express interest in using
ExPOUND to construct learning objects for their own subject areas. The
tool has been developed with inbuilt flexibility to allow for such
cross-discipline use in future.
Work is currently underway to provide an online demonstrator that
lecturers can trial; feedback received will allow the project team to
add enhancements for future versions of the tool. The project also aims
to make the final e-Proofs available as resources on the projects
website, as they are developed. Those who are interested in following
the development of the tool or engaging with the project are encouraged
to follow its progress online at http://www.projectexpound.org.uk/.
Acknowledgments
9
The e-Proofs described here were constructed with the
support of a Loughborough University Academic Practice Award and with
the assistance of Lee Barnett and Keith Watling of the Department of
Mathematical Sciences.
The authors thank Keith Weber and Matthew Inglis for
valuable comments on earlier drafts of this paper.
References
10
Weber, K. (2004). Traditional instruction in advanced mathematics
courses: A case study of one professor’s lectures and proofs in an
introductory real analysis course. Journal of Mathematical
Behavior, 23, 115-133.
Footnotes
11