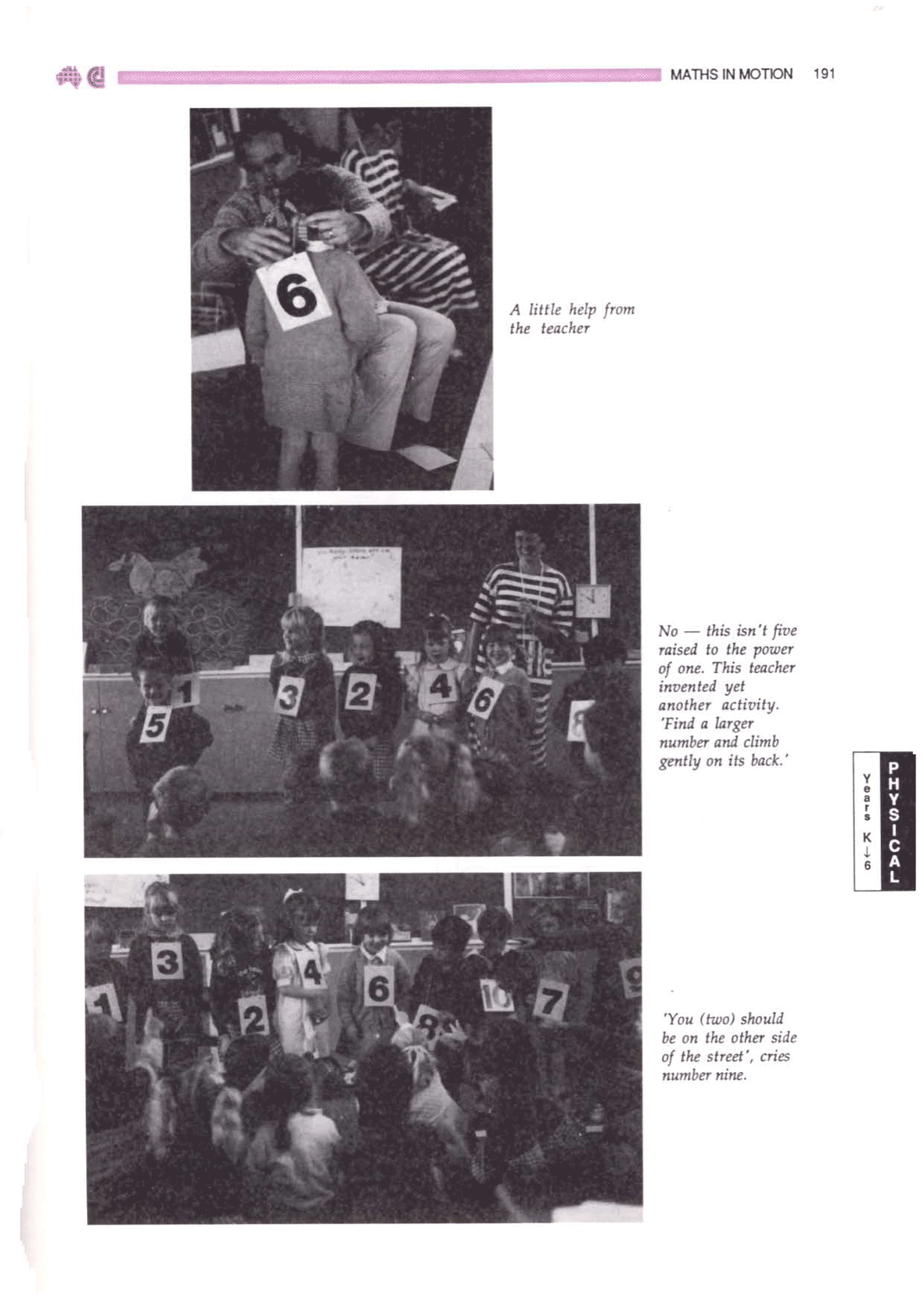A Designer Speaks: Charles Lovitt
and Doug Clarke
The features of a rich and balanced
mathematics lesson: Teacher as Designer
Abstract
1
Look at any 10 classroom lessons. Two might be quite forgettable,
about six might be passable, but one or two might, by general
acclamation from teachers, be considered outstanding.
By analysing what we consider to be high quality lessons, we
contend that it is possible to distil out a set of practical design
features and qualities that are generalisable and transferable to many
lessons. We would claim that in this process, working alongside
teachers, there is the opportunity to empower them to create their own
“rich” and “balanced” classroom lessons.
We will analyse three selected lessons chosen from classrooms.
Each in our opinion passes the test of being both rich and balanced.
What do we mean by rich and balanced?
2
Many authors have attempted to define the term rich in
relation to mathematics tasks or lessons (see, e.g., Downton, Clarke, Knight, &
Lewis, 2006; Flewelling, & Higginson,
2001). Although it is very rare for a single task or lesson to have all
of these features, the following are often mentioned:
- It draws on a range of important mathematical content;
- It is engaging for students;
- All students are able to make a start, as it caters for a
range of levels of understanding;
- It can be successfully undertaken using a range of methods or
approaches;
- It provides a measure of choice or openness, leading to a
sense of student ownership;
- It involves students actively in their own learning;
- It shows the way in which mathematics can help to make sense
of the world;
- It makes appropriate and effective use of technology;
- It allows students to show connections they are able to make
between the concepts they have learned;
- It draws the attention of students to important aspects of
mathematical activity; and
- It helps teachers to decide what specific help students may
require in the relevant content areas, or ways in which students might
be extended.
There are many such lists in mathematics education articles, and
in working with teachers, we have encouraged them to put the lessons we
share with them and the ones they develop themselves under the
microscope, and to ask the questions, “Is this lesson rich? What are the
features which make it so?” These features therefore provide a kind of
checklist, and thus form our design elements in developing lessons. In
the following discussion of three particular lessons, we will summarise
the features which teachers identify in relation to the lessons.
When we refer to balanced, we mean that the features
above work “in harmony”, are mutually self-supportive and not over or
under weight in any aspect. Many traditional text-book type lessons are
arguably overweight in the rush to skill development, while ignoring a
range of other equally important teaching and learning principles. The
balancing act is needed within any lesson, and by implication, across
any set of lessons. We will explore the way in which the three lessons
we discuss can be regarded as balanced.
The three lessons which we encourage the reader to place under
the microscope in this article are titled:
- Temperature graphs
- Maths in motion
- Mathematics of Lotto
In each, we will present a description of the lesson followed by
a critique designed to identify the elements of the design profile, and
also compare and contrast the lesson with an equivalent stereotypical
textbook version.
Our context
3
In the 1980s, there were major concerns with the teaching of
mathematics in Australia, particularly among teachers in the middle
years of schooling (Grades 5-8): We are confident that the following
list generated at that time will come as no surprise to readers:
- Maths was seen as boring and irrelevant;
- Not enough thinking nor genuine understanding was required of
students;
- The topic was too abstract;
- Fear of failure and poor attitudes were evident;
- Maths was seen as elitist, and designed for tertiary bound
students only;
- There was too much content to address and not enough time to
do so;
- Assessment approaches were too narrow;
- Catering for a wide ability range was very challenging; and
- Teachers were struggling with problematic parent and community
expectations.
The authors first worked together jointly running a national
program, titled the Mathematics Curriculum and Teaching Program (MCTP, Lovitt, Stephens, Clarke
& Romberg, 1990). In this project, we had the opportunity to
consider how best to address the above issues, in conjunction with
teachers, mathematics consultants and education systems.
Our response
4
Our focus was, and in many ways still is, to use “the classroom
lesson” as the basis of professional learning conversations. We
attempted to “capture” examples of good practice from around Australia
by documenting lessons, sharing these as “works in progress”, and
encouraging teachers in supportive professional learning environments,
to consider how they could both enhance the lessons, and more
particularly expand their personal comfort zone or repertoire of
teaching strategies. This personal repertoire of features can be called
their design profile—the personal collection from which a
teacher draws in creating (designing) learning experiences.
The model shown in Figure 1 was used as a
basis for these conversations (Owen,
Johnson, Clarke, Lovitt, & Morony, 1988, p. 4.)
Each teacher comes to any learning situation with their personal
current practice or ‘comfort zone’. As teachers worked through lessons
in the role of the student in professional learning settings, and
subsequently trialled them in their own classrooms, they were encouraged
to seriously scrutinise the lessons for the features they contained,
particularly those new to themselves, with a view to ultimately
expanding their comfort zone or teaching repertoire.
In our documentation for a given lesson, which always went
through many iterations, and, in one sense, was never finished, we
attempted to tell the story of the lesson, which was always an “amalgam”
of the ways in which the lesson has played out in a variety of settings.
We used photographs, sketches, samples of student work, comments
from teachers, and insights from trialling to paint the picture of a
lesson, in a way that the reader could hopefully visualise.
MCTP also focused significantly on the professional development
(PD) settings in which these “lesson conversations’” could occur. We
analysed existing PD models from around Australia, developed a set of
criteria for effective PD (see Clarke,
1994) summarised the various PD offerings into eight generic models
(Owen, et al., 1998), and supported consultants and curriculum leaders
to use these as a basis for generating their own local PD settings.
Our work at the time was clearly informed by prevailing national
policy and our understandings of the literature, but was also largely
intuitive and arguably more of a grassroots approach. One memorable day,
a colleague came to us with an article and said “This is what you guys
are on about!” He shared with us the seminal work of Lee Shulman (1986, 1987) on “pedagogical content knowledge”,
or “capturing the wisdom of practice”.
Among the statements which resonated particularly with us and the
work we were undertaking at the time, were the following:
“Teaching is characterized by a collective and
individual amnesia,… the consistency with which the best creations of
its practitioners are constantly being lost to both current and future
peers… It is devoid of a history of practice”
(Shulman, 1987, p. 11).
“Pedagogical Content Knowledge is …an
understanding of what makes the learning of specific topics easy or
difficult: the conceptions and preconceptions that students of different
ages and backgrounds bring with them to the learning of the most
frequently taught topics and lessons … if the preconceptions are
misconceptions, which they so often are, teachers need knowledge of the
strategies most likely to be fruitful in reorganising the understanding
of learners. … the most powerful analogies, illustrations, examples,
explanations, and demonstrations related to the topic one teaches. … the
ways of representing and formulating the subject that make it
comprehensible for others.”
(Shulman, 1986, p. 9).
We realised that in attempting to document the best lessons from
around Australia, we were both highlighting the wisdom of practice, and
encouraging teachers to explore those aspects of pedagogical content
knowledge which could enable a teacher to take a basic idea for a lesson
and make it both rich and balanced.
Our response, which started with MCTP has largely continued in
several follow up projects through to the present. One such current
project using classroom lessons as the basis for professional learning
conversations is Maths300. This is managed by a government agency,
Education Services Australia. Its ambition is to find the 300 most
‘interesting’ (i.e. worthy of professional discussions) lessons from
across Australia and mount these on a website (www.maths300.esa.edu.au) to
be used by teachers and curriculum leaders in various PD settings. All
three lessons discussed here are available to teachers via Maths300.
The three lessons
5
As has been mentioned, our approach has been to introduce the
lessons to teachers in a workshop setting, and then to discuss the
features of the lessons which are evident to them, and which may or may
not be part of their current teaching repertoire.
The lessons are now discussed in some detail. The lessons have
been chosen to reflect a range of design features, different
mathematical content, and different grade levels. For each lesson, we
describe how the lesson might play out (with teachers and with
students), and then discuss the nature of the debrief which occurs with
teachers in professional learning settings.
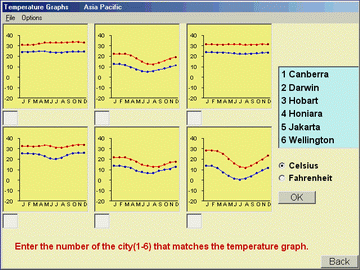
Lesson 1: Temperature Graphs
Teachers are provided with an initial worksheet (Appendix 1), as well as a one-page overview of the
lesson (Appendix 2), and access to the complete Lesson
Plan notes and accompanying software (Appendix 4). The lesson is recommended for
students in Grades 5 to 10.
The lesson
The teacher greets the class and indicates that s/he has a
challenge for them, handing out the worksheet. They then explain the
following:
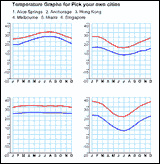
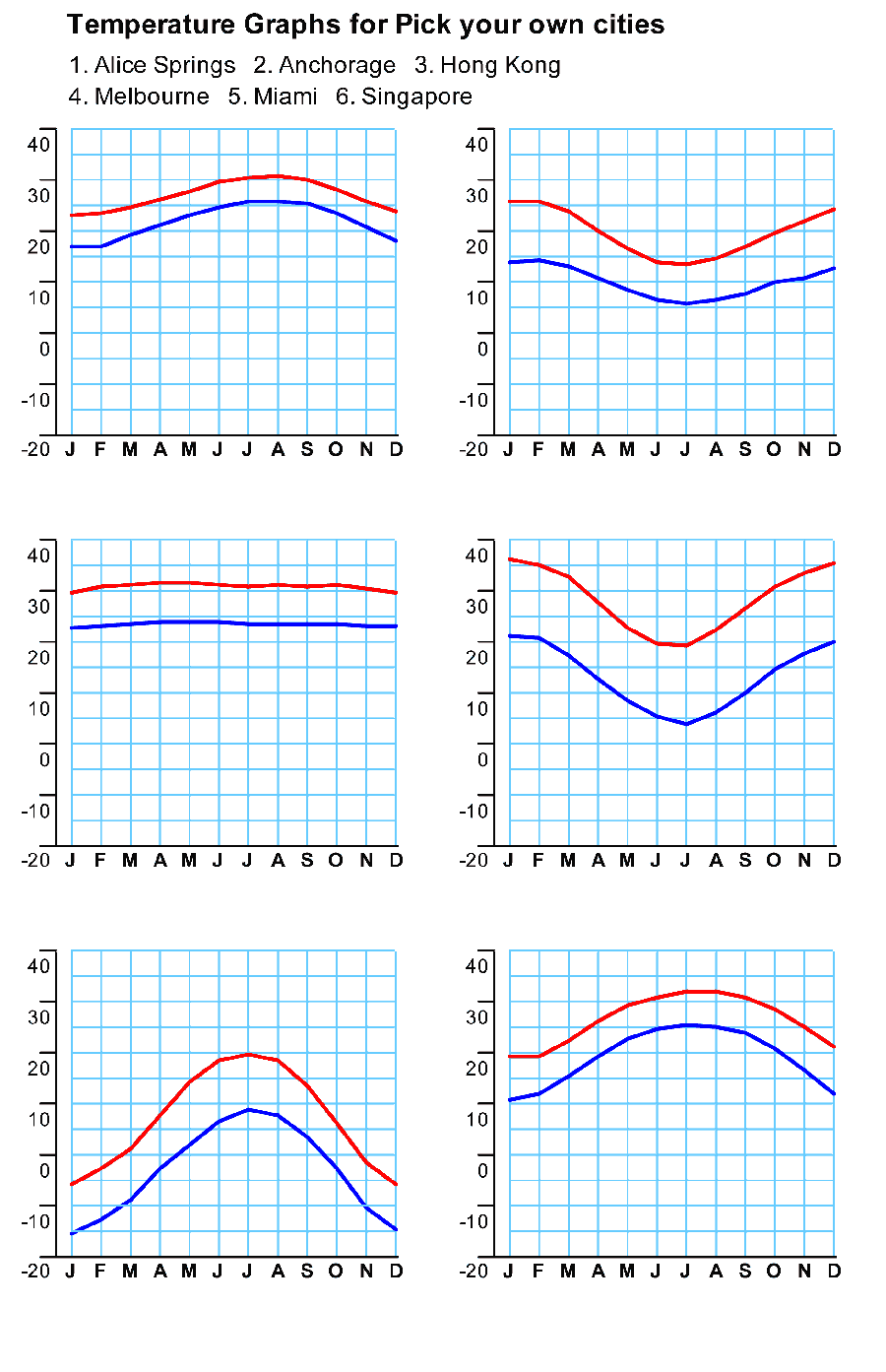
- There are 6 graphs on the page – one for each of the cities
you can see named at the top.
- They are temperature graphs – each one has two lines – the top
graph shows the average daily maximum temperature for each of the
months of the year, while the lower line is the average daily minimum
temperature for each of the months of the year.
- The challenge (in small groups) is to match the graphs to the
cities.
- When appropriate, the teacher pauses the class, summarises the
thinking so far and develops whole class agreement (appealing to the
weather bureau data if necessary for validity).
- The teacher then introduces the software.
- The teacher then uses the “Choose your own cities” option to
reconstruct the worksheet on screen and, once again, encourages the
students to match the cities to the graphs.
- The students then access computers (in small groups), choose
their own cities and answer the challenges they have set themselves on
screen.
- An extension project option is also available as detailed in
the full lesson plan.
The debrief
The following is a typical summary of the debrief discussions.
The first aspect is often to recognise the lesson as different to the
content equivalent stereotypical textbook version, which would be along
the lines of: Here is the temperature graph of some (irrelevant) city.
Answer the following:
- What was the maximum in July?
- In which month was the minimum 17 degrees?
- Which is the hottest month?
- Etc.
Teachers recognised that the purpose of such questions target
just one outcome - namely the skill of correctly reading a scale. In the
alternative version, it was easily noted that this skill has not been
abandoned; it is still there. But now the deliberate addition of some
extra pedagogical features leads to other additional worthwhile learning
outcomes. The additional features which teachers often identify during
discussions include the following:
- Context based. The choice of cities puts a
focus on links with geography and ideas of weather in relation to
location. The context is important and students can learn more about
the world they live in.
- Challenge. Having a challenge is seen to be
engaging. Teachers reported much higher levels of ‘participation’. The
challenge has elements of the intrigue of a puzzle.
- Thinking, reasoning, problem solving. The
challenge requires students to think, argue and justify desirable
outcomes, features missing from the text book equivalent.
- Group work. The higher order outcomes of
reasoning and communication are seen to be developed better by setting
a group challenge rather that an individual one.
- Personal. Teachers reported that students
know something about many of the cities and were keen to share this
personal knowledge. For example, student often ask, “where is
Anchorage?”. If students have personal knowledge to contribute, then
their commitment to the learning is enhanced.
- Technology. The worksheet used initially is
printed from the software drawn from a provided data base of cities.
The capacity to produce multiple worksheets for any combination of
cities, the quick feedback, the opportunity for students to choose
their own questions, the opportunity for research on additional cities
are all aspects provided by the structure of the software. All were
seen to add value to the lesson in ways not available in the more
traditional textbook version.
- Ownership. This was seen as a particularly
valuable feature. In the text book question, the decision on what work
is to be tackled is likely to be taken by some textbook author writing
questions in their home office, possibly 10 years ago. It is this
decision which is largely dictating the journey of both teacher and
student. The software elegantly hands over ownership and control to the
teacher and students. Teachers commented strongly that when students
were selecting cities for their challenges they selected places of
interest to themselves. They had a degree of control over their
learning and were more committed to that learning.
- Skill. As students debate in small groups, it
was clearly seen that the desirable skill of reading graph scales was
still prominent and being developed and enhanced.
- Mixed ability – multiple levels of success.
Some teachers initially commented, “my students might struggle with
this; they don’t know enough about these cities.” But on the software
there is the option to choose just two cities, say Singapore and
Beijing. What do they need to know for success? Singapore is near the
equator and is tropical, Beijing is up north and gets cold.
- Open-ended. An important aspect of being able
to go further and in more depth (if the teachers wants to do so). For
example, “Our school is in Mt. Isa (country Queensland, Australia) and
it is not in the database on the software. But it could be.” Go to a
search engine, put in “Mt. Isa Temperature” and in just a few seconds,
the data will be available. Enter that into the data base as a new city
(and the data will stay there). Then we could put in other regional
cities and produce a worksheet for the class just for the State of
Queensland.
The number of deliberate design features began to look impressive
and as one teacher commented:
“This lesson is now profoundly different,
richer and more balanced that the typical textbook”.
Up until now, the comments and insights from teachers are
deliberately intuitive and informal. Further reinforcement for the
features they have recognised can come from considering formal
curriculum policy documents. One such example is the much respected
International Baccalaureate program (International Baccalaureate Organisation, 2008)
In the IB Middle Years Program (MYP), the section on Teaching and
Learning lists criteria series of statements (Appendix 3) about student
learning. Consider just the first four of these:
Students learn best when: (p. 60)
- their prior knowledge is considered to be important
- learning is in context
- context is relevant
- they can learn collaboratively
Teachers commented:
“This design structure of the lesson exhibits
all four of these – the text book version exhibits virtually none of
them.”
Summary
As indicated earlier, one of the main purposes of the lessons and
the discussion which surrounds them is for teachers to reflect on
particular features of a given lesson, and to consider expanding their
pedagogical repertoire. So, in the case of Temperature Graphs, for
example, teachers might ponder whether they can give their students more
ownership using a piece of software, or by other means. The whole lesson
is also a transferable ‘template’ – the lesson structure, complete with
all its features can be repeated using a different context such as
rainfall, or population growth, or rates of deforestation, or indeed any
measurable commodity that might be presented graphically.
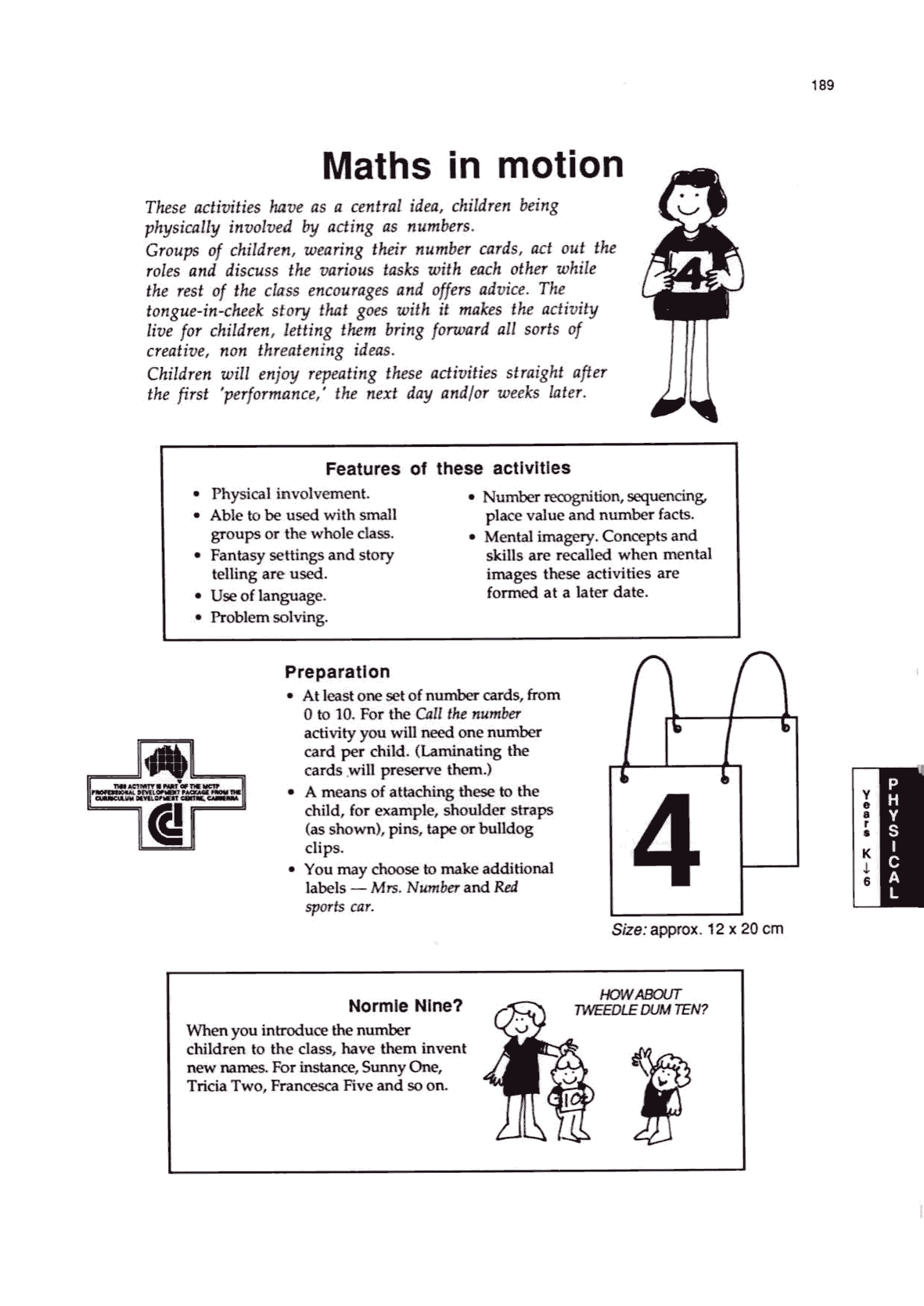
Lesson 2: Maths in Motion
Teachers are provided with an overview page (Appendix 5) and access to the full lesson notes (Appendix 7). This lesson
targets children in grade level K (kindergarten).
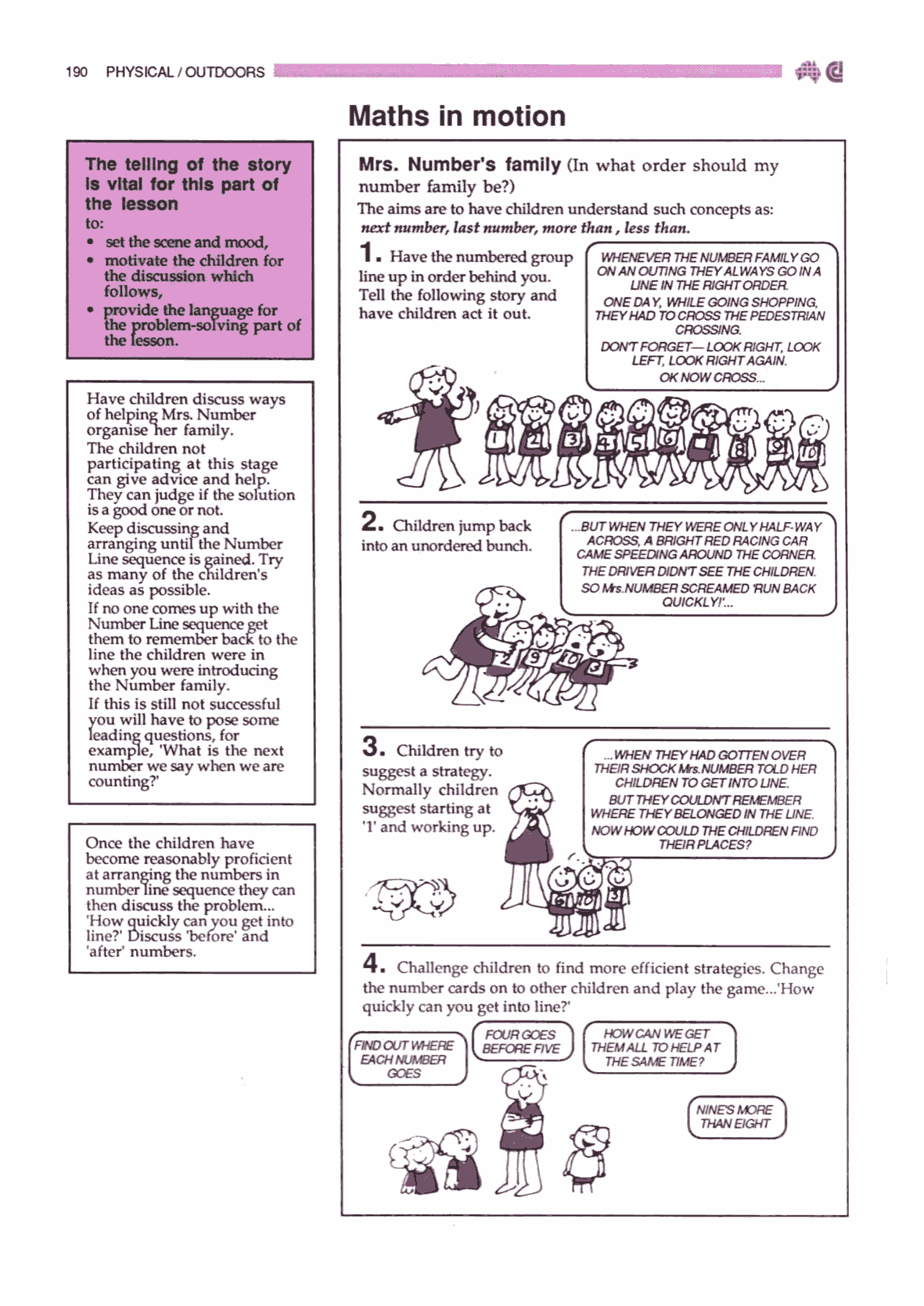
The lesson
The teacher greets the class and invites children to solve some
number challenges for the class, and they get to “be” the numbers. The
teacher then hands out number cards (either 0 to 10 or 1 to 10) for
students to wear. Various stories about ducklings lining up behind
mother duck in order, or finding pairs adding to 11, or rubbish bins in
front of houses are acted out. Each scenario is a challenge requiring
the group to work together. Other challenges can be generated by the
students; e.g., “this group of 3 students are the numbers ‘4’, ‘5’ and
‘8’. What challenges can we create for them?
The debrief
The following is a typical summary of the kinds of features which
teachers identify during debrief discussions.
- Active / physical / personal. All of the
lesson could be done with 10 small numbers cut from cardboard, with all
students working individually at their desk, but the teachers reported
it was far more memorable and involving with students physically
‘becoming the numbers’.
- Group work. Working as a group to solve the
challenges increased both cooperation and communication.
- Storyshell contexts. The ‘fantasy’ stories
about ducklings and other scenarios greatly increased student interest
and involvement – and led to greater engagement with the mathematical
content ideas.
- Challenge, problem solving.
The challenges clearly needed the students to think and reason as well
as learn number skills and facts.
- Creativity. This was seen as a highlight
feature – given the chance to invent challenges caused many students to
peer into the task differently and come up with unexpected yet
profitable directions. Teachers involved in the professional
development also were able to add creative twists and turns.
- Ownership. When tasks were created by the
students and the teachers, the sense of owning the direction of
learning clearly increased involvement and commitment.
- Multiple interconnected content. Some
teachers reported starting with a narrow focus such as ordering numbers
from 1 to 10, but finding themselves in other mathematical territory
such as finding a strategy to find all the different numbers that can
be created by students ‘3’, ‘2’ and ‘8.’ This led to insights about
place value and also combination counting methods.
Teachers’ informal and intuitive judgments can be backed up by
research on effective teaching (e.g., Askew, Brown, Rhodes, Johnson, & Wiliam, 1997;
), and emphases in policy documents. This can give teachers added
confidence that their observations are valid and justifiable. For
example, the emerging (currently in draft form) Australian National
Mathematics Curriculum (ACARA 2010, p. 5) states in a section titled Implications
for teaching and Learning:
In Mathematics, challenging problems can be posed using basic
content, and content acceleration may not be the best way to extend
students. Choosing engaging experiences as contexts for a variety of
tasks assists in making mathematics inclusive, differentiating both for
students experiencing difficulty and those who complete tasks easily.
Summary
Teachers in professional learning settings readily agreed that
each of the features listed above, deliberately designed into the
lesson, added to the overall quality, richness and balance of the
experience. Yet every single feature could have been ignored or
eliminated, as often happens in some resources, where rote learning is
more often the focus. Importantly, teachers agreed that the list of
features by themselves would not be empowering. It is the feature backed
up by the imagery of its use that gives meaning.
Lesson Three: Maths of Lotto
This lesson, currently in development, arose spontaneously
because a mathematics teacher noticed newspaper reports about the social
issues behind citizens over-spending on such things as Lotto Games to
the detriment of their family and financial circumstances. One
hypothesis is that such victims seriously do not understand their real
chances of success and are lured by propaganda and mathematical
half-truth advertising in a desperate attempt to improve their
circumstances. Unfortunately, usually the opposite happens.
So how might a social context like this become a component of a
rich and balanced mathematics program?
The teacher has a repertoire of lesson design features and
considers systematically their use as a lesson structure evolves. The
process is deliberate and systematic.
Recently, one of the authors used this Lotto lesson as part of a
professional development session. It was received extremely well as
teachers responded to its design. One participant commented that it was
a creative way to tackle the issue of gambling. Our contention is that
whatever creativity is exhibited, it is not some sort of artistic
inspiration, but more the product of systematic and deliberate
consideration of the teachers’ repertoire of design features.
Teachers in a professional learning setting are provided with an
overview (Appendix 6), access to the full (draft) lesson
plan notes (Appendix 8) and access to the draft software.
The lesson
Initial discussion of students’ current knowledge of Lotto Games
leads to an invitation to explore the mathematics and the ‘How and Why’
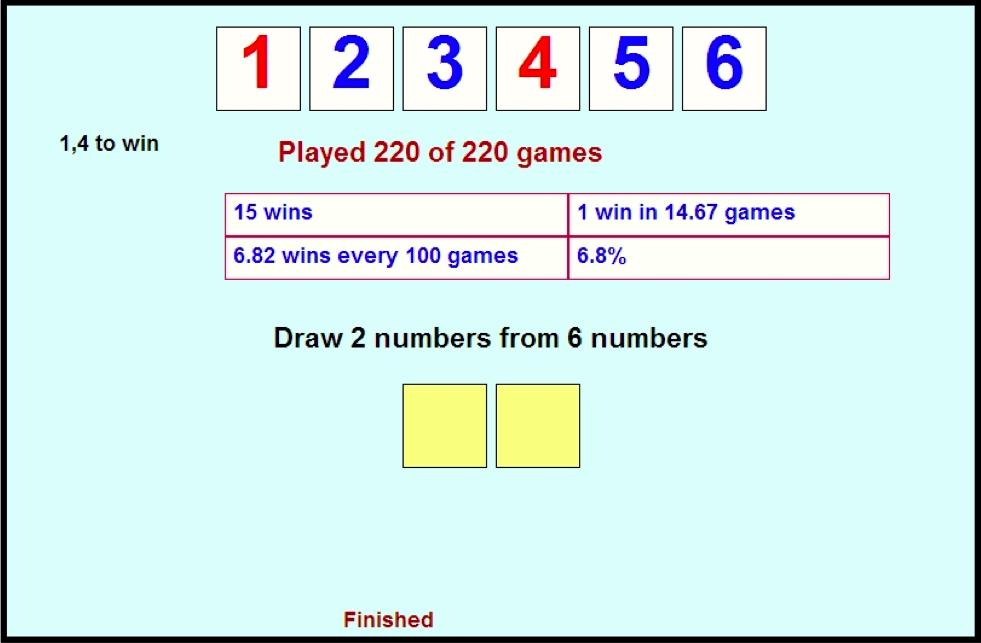
of people losing their money. A simpler version (a 6:2 game) is
proposed, an important ‘estimation’ stage to establish students’
perception of success, then the game is played. This provides class data
which are then analysed to develop underlying key mathematical ideas. A
software simulation significantly supports the process.
The debrief
Firstly, a more typical expository approach might deliver formal
instruction about the mathematics of Combination Theory leading to skill
practice exercises, which may have limited engagement or relevance for
large numbers of students. Redesigning such a lesson into this
alternative investigative approach gives teachers the opportunity to
debate the relative merits of both approaches. The lesson is very
current – and has not yet gone through multiple iterations, but thus far
reactions and discussions have been as follows.
- Social Issue context. The social context of
gambling and the problems this brings combines obvious opportunities to
link mathematics with moral and ethical challenges. It was seen by
teachers as a very relevant context. Importantly, the major outcome of
the lesson is in understanding the context and hopefully being lass
exploitable. The mathematics is not the major outcome, but a pathway to
social empowerment. This is a reversal of text book approaches where
the context is merely the vehicle to learn more mathematics.
- A class game. The 6:2 class game has been a
huge highlight; very engaging and personally involving for students and
a powerful first step towards the investigation that follows.
- Estimation. An important aspect of the lesson
is to find out students’ current perceptions of success. The
investigation is premised on the hypothesis that students will see the
game as easier than it really is. Also, if students make a commitment
to an initial guess, their motivation to find out if their ‘guess’ is
accurate is greater.
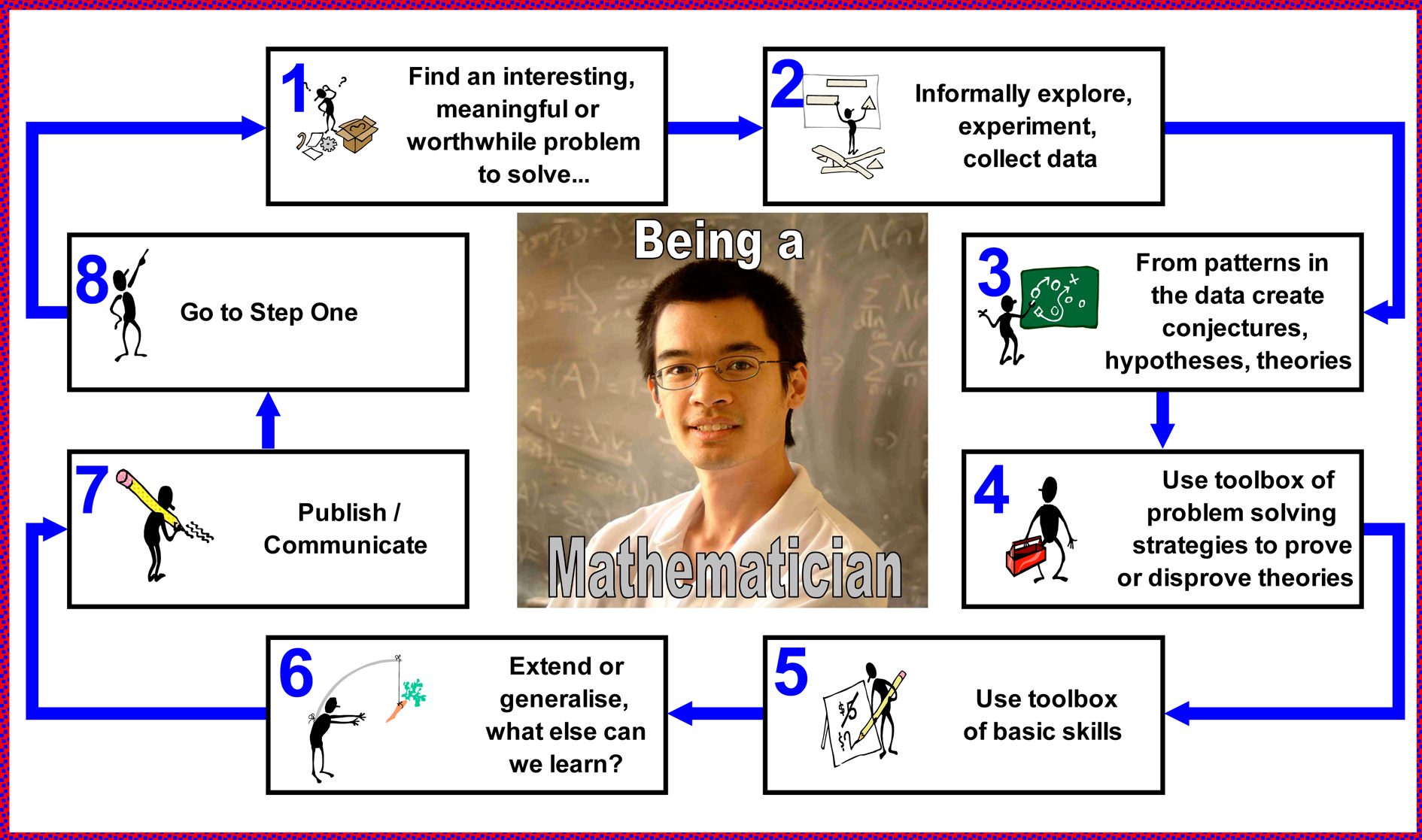
- Mathematical investigative process . How does
a mathematician go about investigating such a context? The attached
poster (Figure 2) has been very effective to highlight how a
mathematician works. [The mathematician in the photo is an Australian -
Terry Tao – a recent winner of the Fields Medal.]
- Strategy. As part of the investigative
process, two problem solving strategies are evident and highlighted.
The real game is modeled (‘make a model’), and also simplified (‘solve
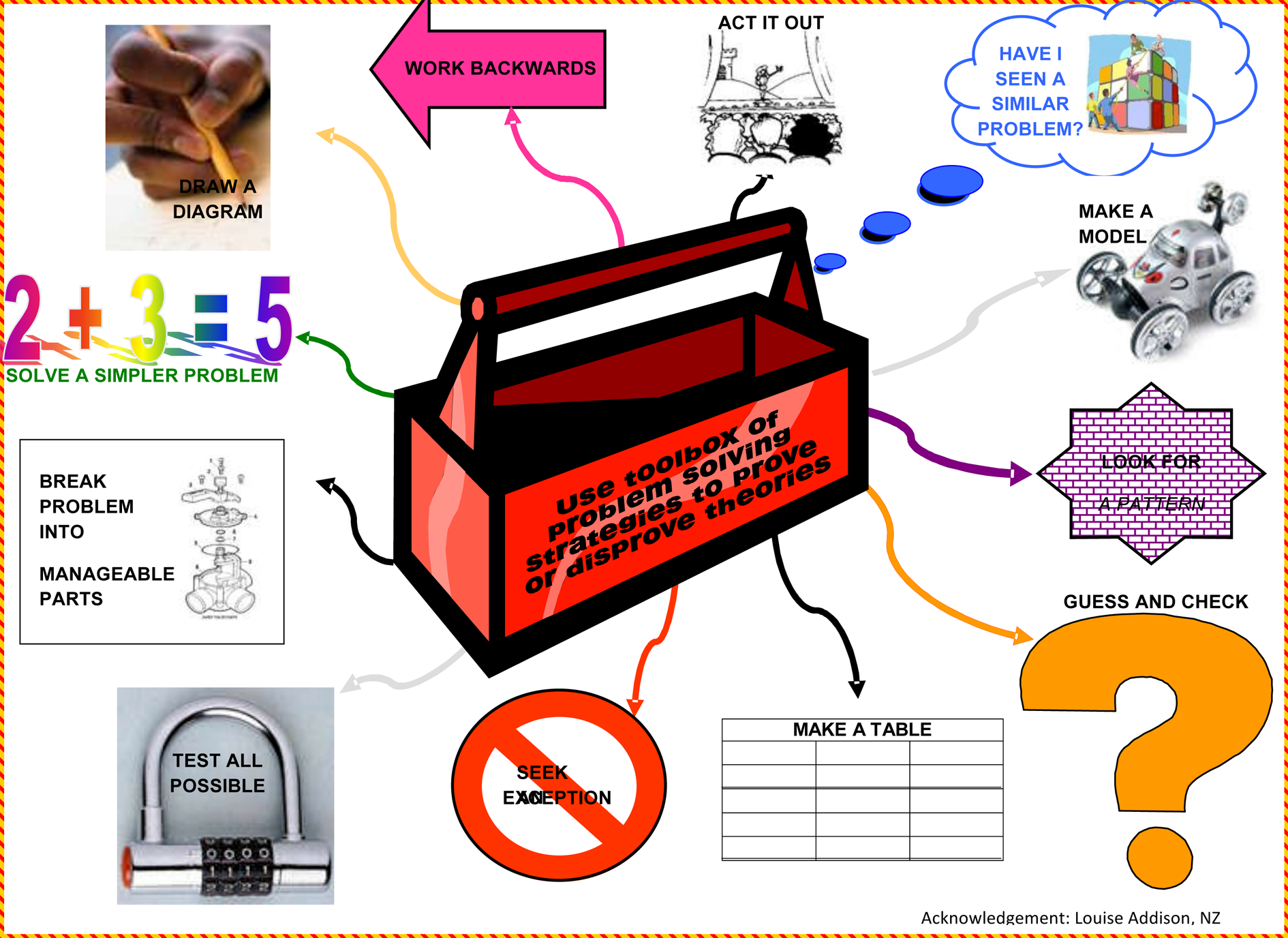
a simpler problem’). The attached strategy poster (Figure 3) is used to
highlight a toolbox of such strategies.
- First principles approach. When working out
the chances of winning the 6:2 game, teachers reported greater
understanding is developed by writing down all the pairs from a first
principles approach than using algorithmic formulae from combination
theory.
- Technology. The software supports the
investigation in important ways, and allows the transfer from the
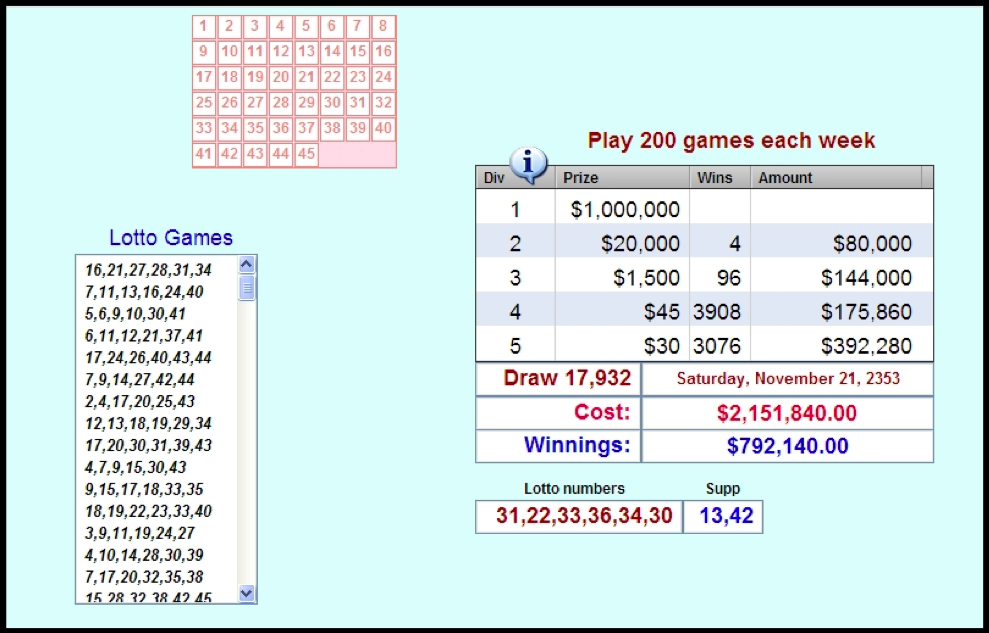
simple 6:2 game (Figure 4) towards the more commonly used 45:6 community context Figure 5).
- First hand data for analysis. Playing the
game produces data and hence is owned by the students. Teachers stated
that this is significantly more valuable than providing second-hand
data from results of other people playing the games (which is what text
books so often do). It is the students’ own data that delightfully
exposes understandings about whether each pair is equally likely to be
drawn.
- Ownership. The software cleverly allows
students to pursue directions of interest to them. If a student decides
they want to find the chances of winning a 8:3 game, the software
allows this. Also, in follow up lessons students decide whether they
wish to play the 6:3 or the 7:2 game.
- Multiple content. There are many
interconnected big ideas of probability and statistics all being
developed concurrently. This is in stark contrast to textbooks that
partition content into separate lessons and hence fail to develop the
interconnections.
- Mixed ability. Teachers strongly stated that
all students were engaged and involved and all felt they had learned
something worthwhile, even though this is different for different
students.
Many of the features of this lesson are advocated within various
policy documents. Once again, referring to the draft Australian National
Curriculum (ACARA 2010, p. 4-5):
The curriculum lists fewer detailed
topics with the intention to encourage the development of ideas in more
depth and promote the interconnectedness of the mathematical concepts…
The … general capabilities of
self-management, teamwork, intercultural understanding, ethical behavior
and social competence are all relevant to the pedagogy used
by teachers of mathematics.
Summary
This last of the three lessons we believe illustrates our general
argument. If teachers wish to create rich and balanced mathematics
experiences for their students, they need command of a pool of design
features. These features may be expressed intuitively, but are backed up
by the imagery of their successful use in other lessons as well as
supported by current research on effective teaching and prevailing
educational policies.
Our design features and their relationship to Pedagogical
Content Knowledge (PCK)
6
When we asked teachers in workshop settings to identify features
of interest within the three lessons described above, and which in their
opinion contributed to the quality of the learning experience, the
descriptors they chose were as follows: The features chosen are
expressed intuitively, informally and are born out of teacher
conversations. We wanted the words used to be ‘teacher words’, generated
by their observations and experiences and not laden with jargon. When
used in discussion, the practical classroom meaning of the (design)
features are illuminated by the context (i.e., lessons) in which they
appear and later mediated through a background learning theory lens or a
system policy lens.
The three lessons and features identified by teachers
|
Lesson 1
|
Lesson 2
|
Lesson 3
|
|
Temperature Graphs
|
Maths in Motion
|
Maths of Lotto
|
- Context based
- Challenge
- Thinking, reasoning, problem solving
- Group work
- Personal
- Technology
- Ownership
- Skill
- Mixed ability – multiple levels of success
- Open-ended
|
- Active / Kinesthetic
- Group work
- Storyshells
- Challenge, Problem solving
- Creativity
- Ownership
- Multiple interconnected content
|
- Social Issue context (community gambling)
- Mathematical Investigative process
- A class game context
- Strategy (solve a simpler problem)
- Estimation
- First principles approach
- Technology
- First hand data for analysis,
- Ownership
- Multiple content
- Mixed ability
|
All the elements from these and other ‘lighthouse’ lessons
aggregate into a single portfolio or personal design repertoire. A
teacher’s confidence in selecting from these to enrich new lessons of
their own design is a function of personal experience, in seeing them
used successfully within a pool or library of lighthouse classroom
lessons.
The teacher is truly an educational
designer.
References
7
Mathematics Curriculum and Teaching Program (MCTP) Activity Bank
– Volumes 1 & 2 (1988). Canberra, Australia: Curriculum Development
Centre.
Stigler, J. W., & H. W. Stevenson (1991). How Asian teachers
polish each lesson to perfection. American Educator, 15(12),
14-20, 43-47.