To address this concern, I recognized that I needed to find a way to explain that the individual task or activity is not the issue, but rather it is its relationship with the mathematical content both before and after the particular activity that affects its meaning and effect. For example, one particular activity in Math 1 (see Figure 1: Algebra Walk ) , which was inspired by an activity in the MCTP Professional Development series) was not included in the new Algebra Connections course even though it was a favorite of students and teachers as a strategy for learning how to graph linear functions by physically embodying points of the function. In this original activity, students were asked to line up on a number marked on a rope representing an x-axis. Students were then prompted to calculate an output value of a function for their x-value and march either forward or backward a number of steps to represent the output of the function for their input value. This activity worked well in Math 1 because it was sequenced within a set of tasks that consistently viewed linear functions as sets of points found by mapping inputs to outputs. In a majority of tasks in this development, students used algebraic rules (e.g., y = x + 1) to calculate outputs for given input values or found algebraic rules to generalize the relationship of non-ordered inputs to given points in a table. With its interpretation of rules as mapping mechanisms, the Algebra Walk was consistent with the unfolding content. Additionally, it offered a surprise that when simultaneously graphing the outputs of a function for multiple ordered x-values (those taken by students on the x-axis), the coordinated result was a line, parabola, or some other interesting shape.

Shaping Mathematics into Compelling Stories
A Curriculum Design Heuristic
Leslie Dietiker
Boston University
Abstract
1This article describes a mathematics curriculum design heuristic that was developed and used in the design of CPM Educational Program textbooks. It introduces a metaphor of mathematics curriculum as a narrative story, which allows for the design of mathematical experiences that emotionally moves students and teachers and compels them to engage. Specifically, it explains how curiosity and surprise can be intentionally designed within a mathematical sequence of curricular elements, such as tasks. Background that spurred the development of the mathematical story framework is offered and examples from designing lessons for Algebra and middle school are provided.
Introduction
2Educational designers regularly make decisions that potentially affect what students learn and how students engage with mathematics (see, for example, Yerushalmy (2013) and Lovitt and Clarke (2011)). However, although recent efforts have led to success in changing the interactivity of students with mathematics, we still know little about how we can methodically design coherent mathematical sequences to stimulate intrigue and curiosity (in contrast with designing an exciting "one-off" activity that is dropped into a sequence). Although designing mathematical experiences so that students spontaneously inquire occurs regularly in science, consistently doing so in mathematics curriculum remains challenging and rare.
This goal, in part, spurred the design heuristic of the CPM[1] Connections textbook series described in this paper. This heuristic, called the mathematical story framework, emerged during our design process as a way to avoid flat, monotonous mathematical experiences for students. Specifically, as the lead writer of the series, I[2] drew on a metaphorical understanding of how literary stories work to engage their readers in order to attend to the motivational dimensions of written mathematical sequences. By viewing mathematical content in narrative terms (as opposed to focusing on contextual word-problem as narrative) my focus was to design mathematical experiences that emotionally moved students and teachers and compelled them to engage.
When interpreting mathematical sequences of statements and problem prompts as stories, this framework draws attention to new questions of curriculum, such as How does this sequence enable anticipation for what is to come? and How can this mathematical story be designed so that the students are motivated to want to know how it ends? It also reframes existing questions about the mathematical logic, such as Does this story make sense? While carefully crafting sequences of mathematical tasks, the mathematical story framework focuses attention to how the content is slowly (or quickly) "revealed" or "obscured" for students. This framework treats the mathematical objects in focus, such as numbers or functions, as mathematical characters. The work with these characters, such as adding numbers or transforming geometric objects, forms mathematical action of the story. The form in which the characters and action are represented can be interpreted as the mathematical setting of the story. For example, the setting of a mathematical story might involve manipulatives on a table, geometric objects created with dynamic geometry software, or symbols on a page. Together, the sequence of mathematical events forms an interwoven plot that can be described for both its form (linear? complex?) and its aesthetic effects (riveting? dull?).[3]
Although I acknowledge that not all mathematical sequences make sense when viewed as a narrative[4], I have found through my design experience that coherent narrative units of mathematics can be designed in ways that potentially will compel students to be interested in how the (mathematical) story will end. Recognizing the potential benefits of this framework for mathematics teachers and other curriculum designers, I drew from literary theory to theorize the mathematical story framework in Dietiker (2013) and defined and illustrated mathematical characters, action, setting, and plot in Dietiker (2015). This current article explains the emergence of a design heuristic associated with this framework and discusses the implications of designing mathematics curriculum using this perspective. To start, I describe the context in which this framework was developed to highlight the qualities of mathematics curriculum that were particularly relevant for its use. After this, I offer more description of mathematical stories and their elements and then describe a design challenge from Making Connections 2 that helps illustrate the framework in action. I also present a set of directive questions that work as a design heuristic to direct the design focus onto the aesthetic opportunities of the potential mathematical stories. Finally, I offer some further thoughts on this design heuristic.
Background and Context: The Emergence of the Story Metaphor
3The roots of this curricular perspective originated from my participation in both the revision of the CPM's original high school written materials (referred to as Math 1) and the genesis of the second generation of CPM high school curriculum (referred to as Algebra Connections). To understand how these two experiences shaped the emergence of this curriculum perspective, some history about CPM curriculum is warranted. CPM began developing mathematics curriculum in 1989 in order to enable teachers to teach the traditional high school content (i.e., algebra, geometry, etc.) through problem solving. Over 30 high school teachers and mathematics educators in Northern California were tasked with developing open-ended tasks that fit within content outlines developed by editors. The overall goal of this new curriculum, funded by an Eisenhower grant, was to connect the thinking and reasoning of problem-solving strategies with mathematical content so that students built conceptual understanding through reasoning and problem solving.
I entered the writing process in 1997 during the revision of the Math 1, which by then was one of three textbooks that I had used in my teaching for several years. My task was to continue the work led by previous writers and editors, namely strengthening the materials by increasing coherence and replacing parts that were not effective. However, a key difference of my work (compared to that of the original writers and editors) was that I had not been part of the original writing team; I did not know the original vision for the content progression beyond what was visible in the textbook and what I could recognize through my teaching of the course. Since many of the problems in the original textbook were generated by multiple authors who wrote activities and tasks without a complete understanding of what would precede or follow, some mathematical problems were related thematically (such as being about a goat grazing in a pasture), but others, while related in content, had little interdependence. While the use of the story metaphor was a long way off, in hindsight I can now recognize how this work involved interpreting the existing mathematical story and trying to figure out ways to strengthen it.
In contrast, when I led the effort to write the Algebra Connections textbook later in 2002, we started entirely from scratch. While relying on what we had learned about task design and addressing the newly adopted California mathematics standards that were in place at the time, we were able to craft an entirely new continuous narrative made up of mini-narratives in the form of lessons. These narrative "chunks" (as we referred to them) were often thematically-interrelated sets of tasks in which we intentionally decided how mathematical ideas would be withheld to create opportunities for surprise and wonder for teachers and students.
It was the juxtaposition of these two design experiences that together enabled the narrative perspective of mathematical content to become visible. That is, mathematical tasks (whether or not they were "story problems") were viewed as part of a mathematical story, as both a moment of the unfolding mathematical content and as contributors to an overarching momentum across a sequence. In addition, in part because of the work of both editing an existing body of work and generating one from scratch, I freely considered how the unfolding of the mathematical content changes when its sequence is altered or when a particular task was replaced with another.
The emergence of the story metaphor became complete when it came time to explain the new Algebra Connections course to teachers and professional developers who were not only familiar users of the original Math 1 course, but some of whom were writers of the original tasks. I was responsible for explaining why particular activities that were much loved by teachers and students were not present in the new materials. Clearly, many reasoned, if these activities were universally appreciated by teachers in many different contexts and led to mathematical gains by their students, then surely it would be sensible to use these activities in the new course!
However, when designing the new Algebra Connections course, we took a different approach to the development of functions. By starting the course with the focus on multiple representations of functions in a way that highlighted how each representation offers special information about the relationship, graphs were viewed as only one way of representing a functional relationship (as opposed to a way of representing related points generated by a rule). Thus, we wanted students to view expressions as a representation of a function that told us something structurally about the function that the other representations did not necessarily reveal. For this new mathematical story, instead of encouraging students to view functions as mappings of inputs to unique outputs, we generated tasks that encouraged students to view a function as a generalized representation of a changing quantity.
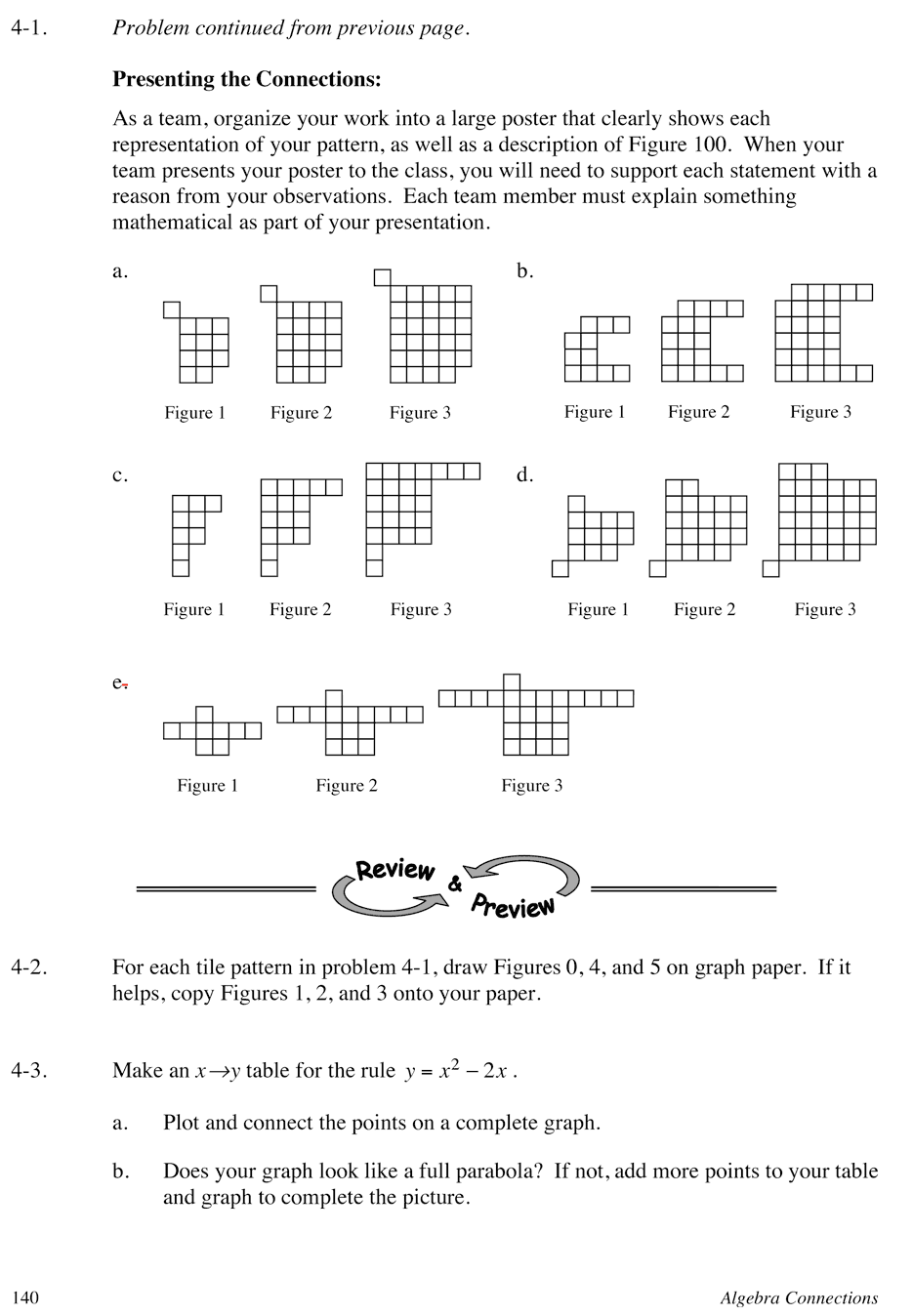
Specifically, the setting of a tile pattern as shown in the Tile Pattern Team Challenge (see Figure 2) was chosen. We decided to start our mathematical story with the emergence of algebraic expressions as a meaningful descriptor of the number of tiles of any term in a given pattern by asking students to predict the number of tiles in the 100th term and, shortly thereafter, the x-th term. This change in the mathematical story altered the meaning of the algebraic representation of the function from a generalization of a process (what do I do to change each input to an output?) to a generalization of a quantity of tiles in a pattern. Since the tile patterns could be interpreted as areas of regions, these algebraic rules generated by students now represent the area of a general term of the pattern (e.g., a rectangle with side lengths tiles by tiles and an additional 1 tile might result in the expression for the x-th term). Graphs became representations of the relationship between figure number and the number of tiles in the pattern and were not the result of a calculation. This change allowed the resulting graph to inform the understanding of the pattern (such as it increases by 2 tiles) rather than being the end result of a calculation. In this new mathematical story, the focus of graphing a rule as an output of each input with a rule would obscure this potential benefit of the multiple representations approach taken in this new course.
Essentially, the Algebra Walk was written out of the new mathematical story and replaced with other tasks consistent within the content development. However, one feature of the Algebra Walk lesson that the writers did not want to lose was its aesthetic surprise. The unfolding of that content led to unexpected outcomes, thus engaging students in wondering about other types of functions. A curricular goal for all activities in the new course was to develop students’ curiosity and surprise in a coherent unfolding of the curriculum. The fact that this activity did not remain in the new course was a result of how the mathematical story involving functions changed and not due to a lack of quality of the original activity.
As I talked to groups of math teachers, it was clear that the mathematical story metaphor was more than a design principle; it had became a conceptualization of mathematics curriculum that enabled our focus to move beyond an individual task or activity to that of a sequence of unfolding mathematical content across tasks and activities.
The Mathematical Story Framework
4As described earlier, it was through these design experiences that the conceptualization of mathematics as a story emerged. The notion of mathematical story pays attention to the mathematical ideas in focus at each point of the sequence to understand how the content unfolds. While not all mathematical sequences can be recognized as narrative, the mathematical story framework was developed and analyzed for how it enables a reader to think about mathematical sequences with a narrative. This theory is written about formally elsewhere (see L. Dietiker, 2013 for more information about how the framing of mathematical story was built from narrative theory) and the elements that make up a mathematical story are defined and illustrated elsewhere (see Dietiker, (2015) for extended discussion on mathematical characters, actions, setting, and plots). In this section, I summarize the qualities of mathematical stories with some additional details that would be of interest to those who design mathematics curriculum.
Just as a literary story can be a short story, a long novel, or a multiple-volume epic tale, the notion of mathematical story also can operate at different grain sizes. Whenever there are a set of connected mathematical tasks or activities in which one can recognize the inter-relatedness and development of the content, a mathematical story can be discerned. Since a lesson can be designed to have developing mathematical events that connect a beginning (i.e., launch) with an ending (i.e., closure), this is a natural unit of a story. However, multiple lessons together can build on each other in a way similar to that of a serial novel in which each lesson is an installment. This means that mathematical sequences of random tasks of different content do not form a mathematical story, just as a random set of unrelated actions do not make a literary story. Viewing large amounts of mathematics curriculum as a giant story offers a way to recognize emergent themes and central characters. For example, a teacher using the Geometry Connections textbook once shared,
‘I remember the second time I finished [teaching with the geometry textbook]. On one of the last days of school we found the equation of a circle using a right triangle. At that point I realized that the whole [geometry] book was about a triangle. The better part of this story was when I shared this realization with my students they all said, “We know.”’
Thus, mathematical stories are coherent sequences of interrelated mathematical events, or changes to the content in the sequence. A mathematical event describes any opportunity in the mathematical story in which the content under study changes. For example, if during a mathematical story a parallelogram is decomposed into parts and then re-constituted into a new figure (such as a rectangle), this change to the parallelogram (who is the mathematical character of this story) is a mathematical event. It is important to note that this definition of mathematical story extends beyond the traditional notion of a “story problem” such as “two trains leave Waterloo Station heading east…”. While story problems such as these are mathematical in nature and thus are included in any mathematical story in which they are a part, the phrase mathematical story used in this paper represents a “narrative take” on mathematical tasks whether or not they are situated in a realistic context.
An important difference between mathematical stories and their literary counterparts involves the actors –– who are they? In a literary story such as Harry Potter (in the books, not in the movie), the term “actor” describes the characters who initiate action. For example, when Harry duels Voldemort, he acts and therefore is an actor in the story. In mathematical stories, however, the characters are mathematical objects, such as triangles and polynomials. It is difficult to imagine a polynomial acting to factor itself. Therefore, in a mathematical story, the changes to mathematical characters are performed by the students and teacher and these changes are examples of mathematical actions. In addition, a narrator/author can perform a mathematical action in a textbook (for example, in a worked example).
The elements of a mathematical story are defined with examples in Table 1.
|
Story Element |
Definition |
Examples |
|---|---|---|
|
Mathematical Character |
The mathematical objects that are discussed and used in the mathematical story. |
y = x + 2, ∆ABC, 0.9 |
|
Mathematical Action |
Something done in a mathematical story that results in a change in the mathematical content. |
The manipulation of a mathematical character (e.g., scaling a triangle or factoring a polynomial) or multiple characters (e.g., adding numbers). |
|
Mathematical Actor |
The people or narrator who performs the action of the mathematical story. |
Textbook author (e.g., a worked example), students (e.g., solving a task or problem), teacher (e.g., advancing the mathematical story through a statement or demonstration) |
|
Mathematical Setting |
The mathematical representation in which the mathematical story is set. |
Physical tiles on a table, dynamic geometry tool, symbols drawn on a paper |
|
Mathematical Plot |
The way in which the sequence of interrelated events reveals and withholds information to increase or release tension. |
A sequence of tasks and activities that supports inquiry from the generation of a mathematical question to the revelation of its answer. |
The Mathematical Story Framework in Action
5As explained earlier, the mathematical story framework emerged as a way of conceptualizing the mathematical development across a sequence of mathematics curriculum, particularly written mathematics curriculum, as a narrative. Specifically, this perspective involves making sense of the ways in which the tasks are informed and changed by the parts of the sequence that came before and come after. This perspective offers new tools for the curriculum designer that can be used to increase the potential coherence and aesthetic dimensions of mathematical written curriculum. In this section, I describe a particular challenge I experienced while designing a lesson in the Making Connections Course 2 textbook. I then synthesize several questions that form a mathematical story design heuristic that can be applied to other design challenges in the creation of mathematics written materials.
A Design Challenge
1To explain how this framework works in the design process, consider the following challenge faced by writers of CPM Making Connections Course 2[5]. As a course developed for 8th grade, one of the content foci was to support the development of a robust understanding of rational numbers. As part of this, we wanted to expose how the structure of a number in its decimal form is connected to whether the number is rational or irrational. That is, we hoped students would recognize that if it is rational, its decimal form must be either integral, terminating, or repeating, while if it is irrational, its decimal form is non-repeating and non-terminating. However, coming to this conclusion was not enough; we were also interested in having students make as many connections between the decimal form and other forms of numbers whenever possible. Therefore, we decided to focus attention on why certain fractions terminate when viewed as the quotient of integers and why others did not. In addition, we recognized an opportunity to deepen student understanding of place-value, which in this case required students to recognize and associate decimal digits for their fractional values (for example, the "2" in 0.25 represents 2/10). Through this content analysis, we created an extensive set of content goals for this mathematical story.
However, we found it challenging to make repeating or non-repeating decimals interesting for students[6]. By and large, the middle school teachers on the writing team were emphatic that grade 8 students are not eager to use long division to study decimal forms and we wanted to avoid relying on computational tools that hid what connects the structure of the decimal with its corresponding rational number written as a fraction. Early on in the design process, we struggled to find a motivation for examining decimal forms in the first place and worried that the activities by and large would become a march through the conceptual terrain by teachers and not by students.
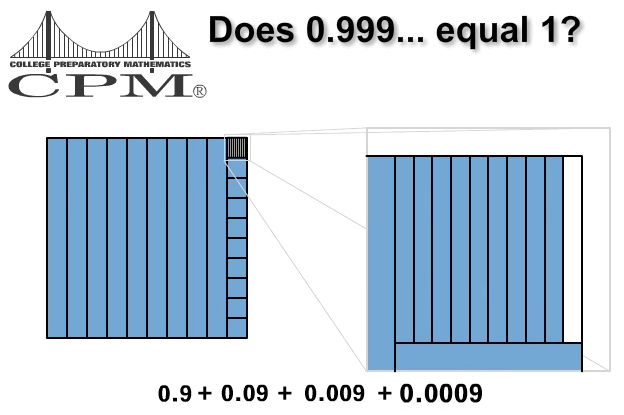
During this discussion, key numbers began to emerge as our central characters. We certainly recognized benchmark fractions and their decimal equivalents as central characters. We also decided that simple square roots, such as √2, would likely be the irrational numbers we would eventually introduce. However, since what was immediately going to follow this lesson was an investigation of probability (which we planned to use as a start of our focus on rational numbers), we eventually came to wonder why the number 1, which would surely a central character of our focus in probability, was not a focus in this story? This question enabled us to focus on what 1 offered to this story, at which point we recognized that 1 has not one but two decimal forms: 1 and 0.999... . Thus, a rich potential for a mathematical plot emerged; what if we could design an activity that challenged students to figure out whether 1 and 0.999... were equal? Since up until this time we suspected students only had seen one decimal form for any given rational number, we recognized the potential for surprise. If we were successful in enabling students to become convinced that 1 can be written both as 1.0 and as 0.999..., we expected that repeating decimals, and thus decimals overall, to gain some respect as a worthy pursuit of study (surely there are other hidden surprises!) that could, in turn, motivate further questions of what we know about the forms of decimals and their relationships to rational or irrational numbers.
With the potential plot twist identified, we started with a task posing the question, "Does 0.999... equal 1?" Given the difficulty of understanding a decimal as the sum of a series of rational numbers and since the study of probability would rely in part on the use of area models, I decided to support the interpretation of 0.9999... as a series 9/10 + 9/100 + 9/1000 + ... and to use the area of a square with sides 1 unit as the representation in which to situate this sum (see Figure 3). Thus the sum of the infinite series could be related to "filling" up the square. Although this strategy discouraged other forms of reasoning that might be readily available to students (such as since 1/3 = 0.333…, and since 3 · 1/3 = 1, then 3 · 0.333... = 0.999... and 3 · 0.333... = 1. So 0.999... = 1), it did support a focus on place value and the view of repeating decimals as a sum of a series. I asked a graphic artist to develop an animation of the square slowly being filled in as each fraction was added in the sum (Figure 3). Since I knew students might be viewing this visual aid, I decided to place the responsibility for reasoning about the sum on the students by augmenting the task with "How do you know? Discuss this with the class and justify your response. Help others understand what you mean as you explain your thinking" (teacher version, p. 56).
Quickly, however, I became dissatisfied with how the mathematical story was turning out. The key question upon which all of this relied was proposed only in the text and was clearly unmotivated. That is, any surprise for the students would be under cut if the students were not attached to the outcome. What could encourage them to care about the potential equality? I had so far done little to invite curiosity by students. I talked to my co-writers looking for ideas of how might this question arise for students before the task that actually poses the question. In other words, part of developing the mathematical story is building pathways of anticipation for students in order for them to not only preempt the text with curiosity to "own" the mathematical question but also to enable surprise when their expectation is not realized.
To deal with this challenge, one of my co-writers, Carol Jansci, suggested that a numerical pattern might enable the snare to emerge unexpectedly. We decided to base a deceivingly simple pattern involving ninths that would encourage students to recognize 9/9 as 0.999… rather than 1. To do this, we started our pattern with 1/9, 2/9, and 3/9 and prompted students to convert each fraction to their equivalent decimal form. Then, by prompting students to extend the pattern for the next six terms for both the fractions and their decimals, we assumed that students would use the pattern of 1/9 = 0.111..., 2/9 = 0.222..., 3/9 = 0.333..., and so on to end up with 9/9 = 0.999... . Since we expected students would also know that 9/9 is 1, this would enable the serious dilemma to emerge. Is the pattern incorrect? Or is 0.999... = 1? We imagined that teachers might have fun with this moment, asking "How does 9/9 = 0.999… when it also equals 1?" and setting up mathematical debates within student groups within the classroom. With something to debate, students can become invested, and thus interested, in the outcome; the answer would determine whether their confidence in the pattern or their assumption about the number of decimal forms a number is ultimately be confirmed or denied.
 Click for complete version (11 pages)…
Complete version (11 pages) available at educationaldesigner.org.
Click for complete version (11 pages)…
Complete version (11 pages) available at educationaldesigner.org.
It is critical to note that it was the withholding of information (that 9/9 can be written both as 0.999... and 1 in the pattern) that enables the surprise. Just as in literature, the plot of a mathematical story relies on building tension between what is known and not known by the "reader," who in this case are the students. When still dissatisfied by the small amount of build-up before the critical moment, preventing surprise, Carol and I settled on adding two additional pattern problems prior to the fraction-pattern problem in order to obscure its purpose. That is, we wanted students to enter the fraction-pattern problem with the anticipation that the point of this problem was about patterns and not about the fractions themselves in order to create the opportunity of surprise. These additional pattern problems were designed to focus the student’s attention on interesting patterns that can emerge with the digits of numbers. With these additional entry problems, the focus was directed to the simple elegance of repeating decimals as opposed to any potential contradiction that might arise. With this addition, our mathematical story was complete (see Figure 4 for the complete lesson with teacher notes).
The Mathematical Story as a Design Heuristic
2Viewing mathematical sequences as a story can enable a writer or editor to look beyond a single task and instead examine the interrelations between the tasks in how content unfolds across a sequence. As this perspective emerged, there were several guiding questions that supported this perspective throughout the design of mathematics curricula. I use the word heuristic to reflect the problem-solving nature of curriculum design. That is, while the designed curriculum might include mathematical problems, the design act is an act of problem solving itself (as shown in the Design Challenge section earlier). Thus, “heuristic” is meant here as a set of generative questions that can be used to work through a curricular design challenge. Note: these questions were not in existence formally during the time of the design work described above, but instead represent a distilled view of the pattern of design that later became the mathematical story framework.
- How does the mathematical content unfold throughout the sequence? Rather than focusing on only the outcome of potential tasks, we shifted our focus to considering the effect of what leads into a task, asking "what way do I orient myself in the mathematical content based on what has come before?" As described earlier with regard to the repeating decimals lesson, we adjusted what came before a task if it can improve the mathematical experience and impact of a task. Often, mathematical stories can be improved with altering the sequence. (See Dietiker (2013) for a detailed description of the re-sequencing of tasks.)
- Where and what are the aesthetic opportunities for students and teachers? Rather than focusing solely on mathematical coherence and content, we additionally considered what the mathematical sequence offered students in terms of surprise or curiosity. That is, what is there to mathematically wonder about? What is there to anticipate? Great stories get readers to wonder and weave questions through that hold all the parts together. For example, we delayed information about repeating decimals to enable students to predict what came next in a pattern, offering surprise and wonder about the nature of 0.999….
- What are the mathematical characters? And which mathematical characters are central to the mathematical story and which are peripheral? We carefully chose central mathematical characters by considering their role. That is, we considered whether the mathematical characters be swapped with others or where there were important reasons in the story to have a specific mathematical character in focus. What are the important qualities of the mathematical characters for the given mathematical story? By recognizing the future role of “1” in later lessons, we recognized its potential role in the repeating decimals lesson described earlier.
- Where is the mathematical story set? Within this framing of mathematics curriculum, we recognized that the mathematical setting enables or constrains the mathematical story. As we considered each potential setting, we asked: What can be learned about the relationships of the mathematical characters and the ways the characters can be acted upon? What cannot be learned? As described earlier, the Algebra Walk setting, with students acting as coordinate points, offered a focus on finding outputs from inputs (for students to determined how far and in which direction to walk) as well as the relationship between the points on the graph (such as recognizing that the resulting points are collinear). Yet this setting did not enable the recognition of how a structured rule represents a generalized quantity. We shifted the mathematical setting to tile patterns in order to support our new mathematical story.
It should be mentioned that in addition to design, this heuristic also helps reveal potential problems with existing designs. For example, in the repeating decimal lesson described above, there is a fourth task (not described above) that was later added at the end of the described sequence. This final task introduces the idea of “terminating decimals” and asks students to identify whether the decimal equivalents of different given numbers terminate or not. In reflection, this task placed at the end of the pattern sequence does little to “close” the story and rather is positioned in a way that could perhaps threaten the satisfaction of the previous part of the story. It’s similar to the extra scene at the end of a movie that you later wonder why it is there; the mathematical story framework helps to reveal that this particular task should have been either changed (to stay) or moved to a different part of the mathematical story.
Also, note that the title of the lesson is also an important part of the mathematical story. When designing the repeating decimals lesson, we worried that a title of “Repeating Decimals” or “Equivalent Forms of Numbers” might give away the punch line of the story. Instead, we wanted to encourage students to enter the 1/9, 2/9, 3/9, … task believing the point of that task was about patterns and not about inspiring a mathematical debate about potential decimal forms of a number. Therefore, we decided to title the lesson “Investigating Number Patterns” to complete the ruse.
Closing Comments
6In this article, I’ve focused the discussion to a design process developed and undertaken prior to the classroom testing of curriculum materials. However, it should be noted that each of these mathematical stories were continually refined through field testing through two years, that is, by the mathematical "story telling" with students. Since I was teaching algebra in a high school, I was able to purposefully test and tweak these tasks based on whether students were excited (or not).
Of course, designing for an aesthetic experience does not imply that all students will experience the aesthetic as intended. Not surprisingly, the individuals experiencing the mathematical story (including both students and teachers) have individual reactions to the mathematical tasks including ways of thinking about the content, degree and focus of curiosity, connections to prior learning, and even what is noticed in the text. Just as a literary story (such as Romeo and Juliet) will not appeal to all the same way, mathematical stories have aesthetic dimensions that will appeal to some and not to others. That said, designing mathematical stories for potential aesthetic moments opens new opportunities for these experiences to include delight, surprise, and other pleasing mathematical aesthetic experiences described by Sinclair (2001).
Often, we wrote teacher notes to accompany our lessons that gave the teachers insight into the mathematical story. For example, once the repeating decimals lesson described in this paper was designed and tested with students, the teacher notes in the written materials informed teachers that:
When the students make predictions about the decimal equivalent of 9/9, expect many students to write 0.9999… based on the pattern, without using their knowledge that (or that 9 ÷ 9 = 1). This is intended to happen, so that students will be surprised when the calculator shows something different.
(Making Connections Course 2, Teacher version, p. 50).
With this notice, we hope that teachers will recognize and capitalize on the opportunity for surprise and inquiry designed in this lesson.
In short, the mathematical story design heuristic offers one way to think through the mathematical story elements to support coherent, aesthetically desirable lessons. It was developed through the experience of negotiating sequences of mathematical tasks and talking about particular parts of sequences in relation to the whole. In my theorization of mathematical stories, I have learned that although the mathematical story perspective is a relatively new phenomenon with regard to curriculum, it has been theorized and used by others. Gadinidis and Hoogland (2003) and Sinclair (2005) have described how this perspective might offer more attention to the aesthetic affordances of mathematics curriculum. More recently, online curricular modules called "3-act plays" have been designed and tested with the notion of a structured mathematical exploration by Dan Meyer (2011). In addition, others have theorized about lesson design as a form of story telling (e.g., Egan, 1988) or play script writing (e.g., Zazkis, Liljedahl, Peter, & Sinclair, Nathalie, 2009). What the work in this article shares with these efforts is a goal to recognize the moment-to-moment unfolding of content through sequential experiences in lessons in the context of the whole so that it may (hopefully) compel and intrigue students to be curious about how the story will end.
Footnotes
7[1] Throughout this article, CPM will refer to the College Preparatory Mathematics Educational Program, which is a non-profit independent publisher in the United States.
[2] As the lead writer and leading manager of both Algebra Connections (at its start) and Geometry Connections and also as a writer and managing editor of the revision of Math 1, I developed the mathematical story metaphor as a design perspective of CPM curriculum. However, this perspective emerged through experiences writing with many co-writers to whom I am indebted. Particularly, I would like to acknowledge the important contributions of Evra Baldinger and Barbara Shreve, who consistently offered amazing insight both as co-writers and co-editors of several of the Connections courses. Others who have helped to shape my thinking about curriculum by early work on the Algebra Connections materials include Carlos Cabana, Susan Baskin, Michael Titelbaum, Bob Petersen, John Cooper, Lew Douglas, and David Gulick. In addition, all of this design work would not have been possible without the incredible leadership and knowledge base in mathematics curriculum in the 1980s and 1990s in California of the original CPM writers, and particularly Judy Kysh, G. Thomas Sallee, Elaine Kasimatis, and Brian Hoey. An additional mention of appreciation goes to Carol Jansci, a writer on the Making Connections series (a middle school series that followed the high school series and from which a central focus of this paper is from) for her help in writing the mathematical story involving repeating decimals described within this article. I should also point out that any shortcomings in this historical description and of this design perspective are entirely my own and not a reflection of this inspiring group of mathematics teachers, mathematics educators, and mathematicians.
[3] I offer more specific description of mathematical stories and their elements in a later section.
[4] The conditions of mathematical sequences to be thought of as narrative are theorized in Dietiker (2013).
[5] I selected this design challenge because it includes the portion of written tasks discussed in Dietiker (2013), an article that theorizes the mathematical story framework from literary theory. Thus, as a companion piece, this article offers a description of the design process that led to the mathematical story analyzed in that article.
[6] I've since learned of additional resources for making repeating and non-repeating decimals as an aesthetically interesting topic, perhaps the most interesting that I'd like to share to anyone interested in Sinclair's (2005) use of a "Colour Calculator" to enable students to see the colorful designs decimals form when each digit is consistently represented by a certain color.
References
8Dietiker, L. (2015). Mathematical story: A metaphor for mathematics curriculum. Educational Studies in Mathematics, 1–18. http://doi.org/10.1007/s10649-015-9627-x
Lovitt, C., & Clarke, D. (2011). The features of a rich and balanced mathematics lesson: Teacher as designer. Educational Designer, 1(4). Retrieved from http://www.educationaldesigner.org/ed/volume1/issue4/article15/
Meyer, D. (2011). The Three Acts Of A Mathematical Story. dy/dan. May 11. Retrieved from http://blog.mrmeyer.com/2011/the-three-acts-of-a-mathematical-story/
Sinclair, N. (2005). Chorus, colour, and contrariness in school mathematics. THEN: Journal, 1(1). Retrieved from http://thenjournal.org/index.php/then/article/view/33
Yerushalmy, M. (2013). Designing for Inquiry Curriculum in School Mathematics. Educational Designer, 2(6). Retrieved from http://www.educationaldesigner.org/ed/volume2/issue6/article22/index.htm