Taking Design to Task: A Dialogue on Task-Initiation in STEM Activities
Abstract
Whereas movement-based STEM learning activities garner increasing interest among designers, researchers, and policy makers, much remains unknown regarding parameters of movement-based activity design affecting learning quality. One such parameter is task-initiation, namely the questions of who decides what should be accomplished with the resources—the designer or the student—and how movement-based STEM learning programs accommodate student choice during task-initiation. In this theoretical paper, we draw on an embodied design theoretical framework to lay out the issue of task-initiation by presenting and comparing two movement-based STEM programs. In both activities, students first perform a task and then model their performance as instantiating STEM concepts, but the programs differ with respect to task-initiation. In one program, the Mathematics Imagery Trainer for Proportion, students learn to perform pre-determined motor-control tasks by developing new perceptuomotor coordinations for enacting goal movements. In another program, Playground Physics, students use real playground equipment, such as a swing, and virtual playground play performances in the app to determine their own task, such as swinging as high as possible. As such, task-initiation design considerations are tightly related to designers’ overall rationales that, in turn, emanate from assumptions concerning, for example, the epistemic constitution of STEM content, the affective allure of STEM practice, manifestations of agency in STEM problem solving, and other contextual details, such as logistical, architectural, institutional, and curricular constraints governing student and teacher experience.
Introduction
This conversation, which started as a critical dialogue between the authors of this article, addresses a proverbial issue in educational design, that of balancing between bottom-up sandbox and top-down funneling to support science, technology, engineering, and mathematics (STEM) learning. Much remains unknown regarding parameters of movement-based activity design affecting learning quality (Abrahamson, Nathan, Williams–Pierce, Walkington, Ottmar, Soto & Alibali, 2020). One such design parameter is task-initiation, which is when learners are orienting to the environment and engaging in embodied learning activities and using digital tools to reconcile their embodied and virtual experiences. As the initial phase in the implementation of STEM learning environments that draw on embodiment theory and digital technologies, the boundaries of task-initiation start when students are first introduced to the task requirements and instructional materials and end with students’ reviews and questions about their initial playful embodied and virtual experiences. Although task-initiation encompasses a mix of different ranges of task controls and accommodations, it spans from a designer-initiated closed task regimen to a student-initiated open-ended task regimen with guided support from an instructor. In this paper, we lay out the issue of task-initiation in two programs: Mathematics Imagery Trainer for Proportion (henceforth, “Proportion Trainer”) and Playground Physics. While in both activities, students first perform a task and then model their performance as instantiating STEM concepts, the programs’ task-initiation designs work with different constraints to meet different learning needs. Whereas the Proportion Trainer offers designer-initiated task regimens along pre-specified conceptual landmarks that allow students to learn to perform pre-determined motor-control tasks by developing new sensorimotor coordinations, Playground Physics offers student-initiated task regimens within which they interact both with real playground equipment, such as a swing, where each student determines their own task, such as swinging as high as possible, and with virtual playground equipment, which included analytic augmentations, in the app. Our focus on task-initiation is to describe who gets to decide what movements to enact and how these environments accommodate student choice, and discuss the implications of those design choices, to illuminate the theoretical distinctions guiding the decisions and the practical implications for student learning experience and teacher experience.
Designing for Embodied Learning
A recent confluence of three interdisciplinary developments—in philosophy of cognitive science (the embodiment turn), human–computer interaction (naturalistic interfaces), and research methods (multimodal learning analytics)—has been accelerating innovative educational research on the role of the body in content learning (e.g., Jewitt, Price & Sedo, 2017). This embodied turn in the cognitive sciences has stimulated new insight into students’ enduring learning challenges, specifically in STEM disciplines (Pouw, van Gog & Paas, 2014). Taking on these challenges, researchers have offered empirically validated principles for building activities that ground content learning in embodied experience (Fugate, Macrine & Cipriano, 2019; Lee, 2015; Skulmowski & Rey, 2018; Tran, Smith & Buschkuehl, 2017). Within this broad scholarship on the application of embodiment theory to STEM education, this article contributes specifically to the literature about engineering and evaluating activity architectures centered on movement-based STEM learning. We have chosen embodied design for a discussion of task-initiation, because we are invested in evaluating and improving the design of STEM learning environments that draw on embodiment theory and digital technologies.
The embodied design framework is suitable for creating activities that promote content learning in various STEM subject areas, including chemistry, biology, physics, material science, and mathematics (Abrahamson & Lindgren, 2014). The embodied design framework delineates a procedure for creating STEM learning environments that anchor students’ cognition of targeted content in their solutions to problems they encounter in the course of attempting to perform physical activity tasks. In embodied design activities, learners make sense of situations by first drawing on their tacit perceptuomotor capacity, then encountering the disciplinary analysis on the same situation, and finally reconciling these competing views as complementary. First, learners encounter interaction problems that require them to figure out how to enact a particular new movement form. Then, they use formal STEM instruments that suggest a complementary yet non-contradictory disciplinary framing of the same situation. The formal disciplinary view highlights latent features of the situation that had not been available to the child’s primary intuitive view of the situation yet are critical for developing the formal understanding. Embodied design activities often depend on teachers to facilitate and optimize students’ engagement and, in particular, to support students’ considerations of the formal perspective on situations and reconciliation of the formal explanation and their intuitive view (Flood, 2018; Shvarts & Abrahamson, 2019).
Situating Embodied Design Among Related Frameworks
Design-based educational researchers have developed a plethora of design steps for building environments that foster math and science learning via participation in embodied activities. The principles are generated from the design either of a single project and technology (DeSutter & Stieff, 2017; Enyedy, Danish, Delacruz and Kumar, 2012), several projects and technologies (Lee, 2015), or multiple projects and technologies for a specific content area (Abrahamson et al., 2020). These heuristic design principles are continuously evolving in light of multiple factors, including the emergence and adoption of new technologies, rising disciplinary domains of application, consideration of more diverse learners, critical feedback from users, and potentials and constraints in informal and formal learning environments.
The two design projects selected for this article on task-initiation are arguably representative of the similarities and differences across educational research and development efforts drawing on embodiment theory, and, therefore, any insights gained herein possibly apply more broadly to the field. We determined the representativeness of the two designs across the field by surveying publications that offer overviews of the field’s state of the art. We found at least three common design steps that were aggregated from projects across a variety of content areas and technologies and are broad and tightly aligned with the aim of supporting the entire process of STEM teaching and learning in both formal and informal learning environments. The steps are aligned with the task-initiation of the two programs described in this article.
1. Determine embodied learning goals and tasks
Determine embodied learning goals and tasks that solicit students’ tacit sensorimotor capacities, viz. their innate or early-developed goal-oriented cognitive inclination either to perform perceptual judgments of the sensory manifold or build new motor coordinations for enacting ecologically coupled movements. This unmediated step allows students to draw on their everyday understanding of the world around them in their attempts to solve embodied interaction problems that arise in the course of tackling the activity task. In this first pre-symbolic activity step, students approach an interaction task intuitively, relying on informal engagement and sense-making with a situation that presents no overt formal signs denoting practices of the STEM disciplines. In the course of attempting to perform the task, they come up against a problem, whose solving constitutes the learning goal. This step stipulates at the outset specific embodied performance tasks, such as collaboratively modeling the structure of a molecule as a hand-in-hand concatenation of proximate human bodies (Enyedy, Danish and DeLiema, 2015); running across the floor in pursuit of a meteor flying along a bending trajectory through the solar-system’s planetary gravitation field (Lindgren, 2015); enacting bees’ foraging and communicational behaviors in interaction with fellow bees (Danish, Humburg, Tu, Davis & Georgen, 2018); or walking together in uniform angular velocity as a single geometrical ray revolving around a common landmark (Zohar, Bagno, Eylon & Abrahamson, 2018). Typically, this activity step ends when students achieve a significant task-performance criterion, that is, they have progressed almost as far as possible given their naïve intuitive wherewithal (cf. Gigerenzer & Brighton, 2009).
2. Introduce mediating resources
Introduce mediating resources that have the potential to perturb and shift the learner’s unmediated actions. This step involves the interpolation of STEM instruments—features such as diagrammatic or inscriptional overlays and tools—onto the activity space (Abrahamson, 2012). Learners can identify embedded utilities in these new features that enhance the enactment, explanation, or evaluation of their own unmediated solution strategies.
3. Facilitate student negotiating and reconciling of embodied experiences
Facilitate student negotiating and reconciling of their playful embodied experiences, in addressing initial movement problems, with the use of instructional materials, including mediated resources. This involves subtle cognitive imbrications of unmediated and mediated ways of doing, thinking, and talking; it calls for nuanced interaction with expert pedagogical agents, who apply a variety of discursive resources that enable learners to mind the epistemic gap (Shvarts & Abrahamson, 2019). The instructional support may include “physical cueing and situated real-time feedback….[in the form of] physical demonstration, co-production, hands-on coaching, as well as using media technologies to present audiovisual and even haptic experiences that convey expert perspectives” (Abrahamson & Lindgren, 2014, p. 365). In particular, this step is designed to help learners to gain access to, reflect on, and coordinate their personal array of possible solutions, creating opportunities to deepen their initial understanding of STEM concepts.
Task-Initiation in Proportion Trainer and Playground Physics
When students are first introduced to embodied learning activities that rely on digital technologies, they often require some rudimentary orientation to the environment and its instrumentation. The designer or teacher familiarizes students with the functionalities of the digital tools, including how to control them, how to use them to perform or record actions, what forms of feedback to expect, and peripheral features of the environment to ignore because they are irrelevant to normative tasks. Interleaved into this activity-orientation phase could be a stipulation of a task, where the stipulation could vary from the general to the specific, for example, use these crayons to draw on this paper: …anything you want; …a picture of an animal; …a picture of a dog; …a picture of your favorite dog; …a picture of your favorite dog running in the park; etc.
The critical point we wish to explore is whether and how this issue—the student’s degree of autonomy in task-initiation—is important. Does it matter for children’s development and learning who gets to specify the majority of activities in the task-initiation phase—whether it is they or the teacher/designer who designate what has to be initially achieved in the environment and, therefore, what criteria will be applied to determine the quality of their engagement with the activity? These are some of the questions motivating our examination of task-initiation as a focal design dimension of interest for this article.
In general, the design dimension of task-initiation can be viewed as spanning two antipodes: (1) a designer-initiated closed task regimen, where students are required to figure out how to perform a particular movement form that solves a pre-articulated motor-control problem; and (2) a student-initiated open-ended task regimen (“sandbox”), in which students are asked to set their own embodied tasks, along with task goals and activities, and the design of both software tools and curriculum activities accommodate a panoply of students’ interest-driven goals and physical activities, including using one’s wheelchair to engage in motion, force, and energy activities. Between these positions lie a variety of learning environments, such as those that are a mix of different ranges of task controls and accommodations.
In this conceptual paper about task-initiation, we aim to unpack some design deliberations that guided choices about this issue in two different programs. Focusing on two designs that both begin with children enacting physical movements, we will describe who gets to decide what movements to enact and how these two environments accommodate student choice. We discuss the implications of those design choices, to illuminate both the theoretical distinctions guiding the decisions and the practical implications for student learning experience and teacher experience.
In Proportion Trainer and Playground Physics, students first perform a task and then review their movement performance with the goal of accomplishing it for ultimately learning about ratio or physics. However, the activities in these instructional programs differ with respect to task-initiation. In the Proportion Trainer, students learn to perform pre-determined motor-control tasks by developing new perceptuomotor coordinations. In Playground Physics, students undertake play performances, such as swinging, running, or throwing a basketball, within which each student determines their own task, such as swinging as high as possible, running as fast as possible, or getting a ball through a basket. Clearly, these two embodied-design activity regimens differ starkly with respect to student choice during task initiation. And yet each activity is following its own logic that guided the design of its respective activity regimen. An objective of this paper, thus, is to complexify any preconceptions that educational designers might have about some would-be universal truism concerning what constitutes a preferred design choice. In the next section we will provide for each program an overall description, including its learning goal, approach, and key program components; and explain in detail how it involves students in task-initiation.
Description of Proportion Trainer
What is the purpose of the Proportion Trainer?
In the landscape of technological resources for mathematics education, Mathematics Imagery Trainers are quite unconventional. The design rationale of Trainer activities is based on an epistemological premise, coming from embodiment theory, that conceptual knowledge is essentially a form of perceiving the world so as to act on it. As such, the “cake” of learning a new mathematical concept is learning to attend to the environment in a new way that lets you move in a new way, whereas the symbolic and algorithmic descriptions of these perceptions and actions, so critical to mathematical practice, are more like the “icing” on that cake.
Consider the following example. What might it mean to understand the mathematical notion of proportionality? One might present a sequence of number pairs, such as 1:2, 2:4, 3:6, 4:8, 5:10, and so on, and draw students’ attention to the constant multiplicative relation of x:2x in each number pair. Often, teachers create a two-columned ratio table, with the ratio pairs running down. In this example, the left column would be 1, 2, 3, 4, 5, …, and the right column would be 2, 4, 6. 8, 10, … Typically, these tables highlight additive rather than multiplicative properties of proportional progressions: the constant increments down the left and right columns, respectively, and perhaps also the increasing difference between the two numbers in each row. Students can use their robust knowledge of addition to evaluate and predict ratio pairs. What they are less likely to experience, though, is the essence of proportion, which, again, is the invariant multiplicative factor.
Some teachers use activities for grounding the mathematical notion of invariant ratio in sensuous experience. They show, or let students discover, how mixing colors of constant ratio, say 1:2 quantitates of blue and yellow paint, results in a consistent mixed color, whereas violating the ratio, such as 3:4 or 2:5, would make the green “too blueish” or “too yellowish.” Analogously, constant ratios of flavor constituents, such as lemon, sugar, and water, yield mixtures of identical taste, whereas getting the ratio wrong will make the lemonade too sour or too sweet.
Whereas these compelling experiences focus on comparing ratios, the Trainer, instead, focuses on the transformation from each ratio to the next ratio—what we need to do to a number pair so as to change it into another number pair bearing the same multiplicative relation. An impetus for this approach is that students tend to add equivalent amounts to both sides, such as 1:2, 2:3, 3:4, 4:5, etc., which keeps constant the difference in each ratio, and yet in proportion what remains the same is not the difference but the multiplicative factor. Keeping the multiplicative factor constant is not intuitive to students, because they don’t have any way of sensing this sameness as a property of the situation that they can enact. By “enact” we mean that Trainers conceptualize mathematical concepts as grounded in ways of perceiving a situation so as to move in some particular way that has been designed to express the mathematical concept in question—students are to move in a new way before they make mathematical sense of this new way of moving. Thus, Trainer activities seek to introduce to students a new way of feeling something that is the same across a set of proportionate ratios, and this is done, initially, without any symbols at all, and, in fact, without any discrete quantities whatsoever.
Readers interested in the Trainer’s theoretical foundations in the literatures of mathematics education, the learning sciences, and movement sciences, are referred to our project website, which includes information about empirical evaluations of the Trainer activity architecture across several mathematical concepts. See, in particular, Abrahamson (2019) for an overview of the ten-year project, Abrahamson and Bakker (2016) where we argue for a role of movement in mathematics learning, and Abrahamson and Abdu (2020) which compares our rationale with that of other Dynamical Mathematics Environments, such as GeoGebra.
What is it and how does it work?
For a quick dive into the Trainer, interact with the online app at https://phet.colorado.edu/en/simulation/ratio-and-proportion. Alternatively, try this. Lay your hands flat on a desk. Unknown to you, the designer has designated the desk as the zero line, and each hand will soon be moving up and down along a vertical axis that depicts its quantitative magnitude relative to the other hand. Now raise your hands so that they are at 1:2 heights, that is, to locations above the desk, in the air, where your right hand is double as high from the desk as your left hand. Next, moving both hands simultaneously, see if you can raise them farther, keeping constant the 1:2 ratio between their heights. Most people, upon first trying this, raise their hands at the same rates, whereas, in fact, the right hand should be moving faster than the left hand. Note that students who participate in this activity may have never studied proportion. In fact, they might not even know that they are engaged in a mathematics activity, because there are no standard mathematical signs in this environment. So how do we even communicate the task to them, and how do they monitor their actions? This is achieved by implementing this bimanual activity in technological platforms, such as tablets or remote-sensing devices, that can give feedback on the hands’ location – green if you’re in a good place and red if in a wrong place, with green-to-red color gradients helping you find the good places. Your task, then, is to find a green place and then move both hands, keeping in green. Thus, the Proportion Trainer is a digital puzzle that users solve by figuring out how to move in some predefined way as a cognitive entry into understanding the mathematical concept of proportional equivalence.

Enlarge…
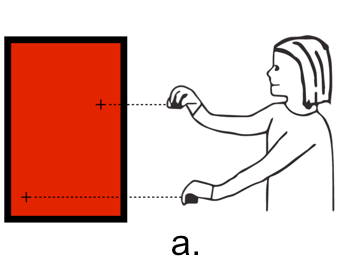
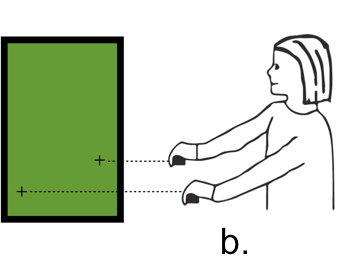
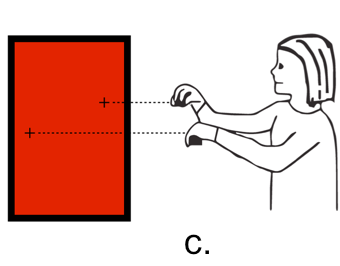
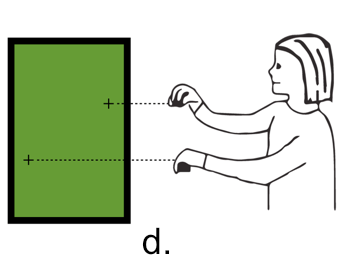
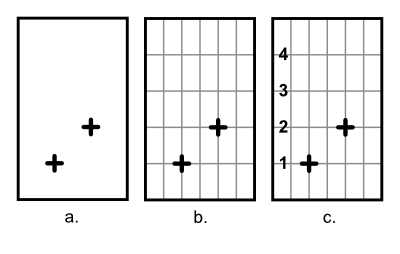
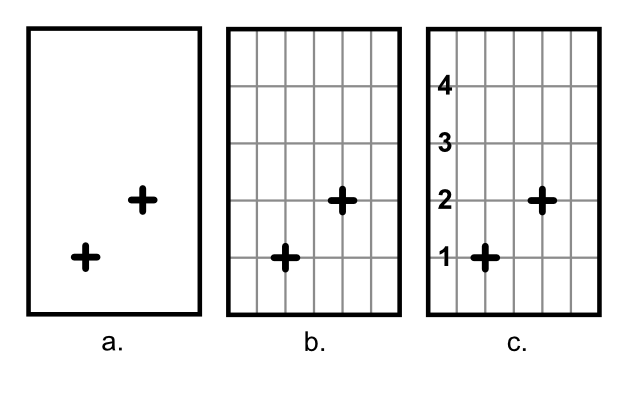
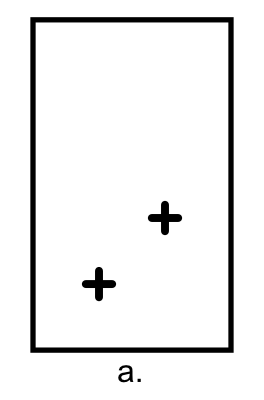
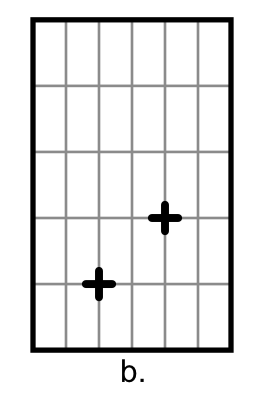
Figure 1 shows a student working with a remote-sensor version of the Proportion Trainer. The respective heights of her hands above the screen base correspond to a ratio. Initially (Fig 1a) she places her hands at an arbitrary location. She receives red feedback, because the ratio, about 1:5, is not the solution to this particular puzzle item. Moving her hands up and down, eventually (Fig 1b) she happens to place her the cursors at locations corresponding to the goal ratio of 1:2, and so the screen turns green. Her challenge, then, is to move both hands, keeping the screen green. She asks herself, “What can I keep the same here, as I move both hands?” She believes that she should keep the distance between the cursors equivalent, and so (Fig 1c) she raises her hands thus, violating the ratio and consequently resulting in red feedback. Eventually (Fig 1d), she figures out that the distance between the cursors needs to change. She might say, “The higher my hands, the bigger the distance.”
How does the task-initiation process work in the Proportion Trainer?
The initiation task is hermetically designer-initiated and designer-controlled, because the designer wishes to ensure the likelihood that students will enact the specifically targeted movement form to ground the concept of proportional equivalence. In the task-initiation phase, students are: (1) introduced to the tool: (2) presented an embodied interaction problem (keep the screen green), and (3) provided instant feedback as they explore how to move in green.
Familiarizing them with tool. Students are seated at a desk across from a tall vertically oriented screen and are handed two tracking devices, one for each hand. In this step, they can recognize that the two cursors that appear on the screen are mirroring their hand-movements. They can gain a better sense of the activity space—the spatial window wherein their gestures affect the color of the screen—and thus, become more acutely aware that their hands’ locations are governing the color. Throughout the task-initiation phase, there are no numbers or any other markings on the screen.
-
Exploring making green. Once the instruments and basic mechanics have been introduced, students are presented an embodied interaction problem, that is, figuring out how to make the screen green. Although they are asked to move the two cursors on the screen, they are not told that only one movement form is positively sanctioned as favorable. This particular movement form is entrained through immediate technologically-generated feedback. The color changes by gradients from red—“failure”—through to green—“success,” according to computational approximations of performance quality. In fact, there are numerous “green” locations, and the student needs to figure out how to coordinate the movement of the cursors in constant green, viz. how to move the hands in a continuous dynamical “success” state.
The coordinated actions of both hands and positioning them at particular stable locations are necessary to achieve green in the activity space. When students first begin the activity, they often work with only one tracking device at a time. Then, they may wave both hands up and down in the same direction, followed by moving them in opposite directions. They also experiment with moving one or both hands at different speeds. All these movement forms are exploratory in nature and subjected to a dynamic feedback regimen to train the student in making green.
Moving in green. Working in the continuous-space mode, students are guided toward moving in a prescribed form. No other form is ultimately acceptable. In the case of the 1:2 ratio, the collection of green locations will pair the right-hand (RH) cursor at a position that is double as high up along the vertical axis of the screen as compared to the left-hand (LH) cursor. Note that for every LH location, there is a RH paired location that would make the screen green. Thus, the student can move their hands up and down the screen from one green location to the next, keeping the screen constantly in green. Moving both hands thus, up and down the screen, maintaining the RH-to-LH “success” positional pairing, requires moving the hands at different rates (e.g., for a 1:2 ratio setting, RH must move up along the screen double as fast than LH). One way to execute this bimanual movement is by attending to the spatial interval between the hands, increasing this interval as the hands rise and decreasing it as they descend (in Figure 1, compare the distance between the cursors in images 1-b and 1-d). At the same time, note that in moving their hands this way, the heights of the students’ LH and RH above the screen base are always related by the same a:b ratio, here 1:2. Thus, even as the students are enacting the solution movement by attending perceptually to the distance between their hands, this movement instantiates an a:b proportional progression up and down the screen.
Enlarge…
Once students are able to move in constant green, which is programmed to instantiate proportional equivalence, the activity facilitator instigates the next design phase, which is not part of the task-initiation, but is the process in which students can start to re-perceive this movement from a mathematical point of view. To shepherd this re-perception, the facilitator introduces digital elements overlaid onto the manipulation space (see Figure 2) that supplement (a) the cursors with (b) a grid and, finally (c) numerals. Each supplementary element introduced onto the screen is designed to disrupt the student’s previous enactment of the movement form by suggesting new opportunities for engaging in the activity, recruiting dormant schemes, and thus shifting the student’s perception of the environment to a point where they may reconfigure their enactment strategy. The activity facilitator then engages the student in a summative conversation about their various solution strategies and how these strategies may be related. For examples of the rich connections that students make between their strategies, see Abrahamson et al. (2014)
Description of Playground Physics
What is the purpose of Playground Physics?
The goal of Playground Physics is to make physics learning accessible and fun for middle school students, especially for those who may not be interested in science learning, find it to be a challenging and boring discipline, and do not identify with the field of science. Related factors contributing to this disengagement include the popular conceptions of physics as a “serious” and rigorous academic business, as concepts that are typically unrelated to students’ everyday experiences and highly abstract, as rote memorization of facts to be regurgitated, and as problem-solving recipes (Britner & Pajares, 2006; Wieman & Perkins, 2005; Zeyer et al., 2013). To address this challenge, the New York Hall of Science (NYSCI)—a hands-on science museum—conceptualized and designed the Playground Physics program integrating informal and formal science learning strategies to improve diverse students’ engagement and learning about science (Honey & Kanter, 2013; Russell, Kehoe & Crowley, 2017). Playground Physics aims to combine the engagement and motivational qualities of informal learning environments and academic learning of physics in the classroom. Fine (2014) argues that “cognitive rigor matters deeply, but so does the affective experience of engaging pleasurably in academic work. To ignore the importance of either of these dimensions when it comes to learning is to do students a grave disservice” (p. 4). Towards this end, Playground Physics activities—infused with the sensibilities of informal science learning environments—seek to give students a grounded window into physics learning by offering them multiple playful ways (physically, emotionally, and cognitively) to explore physics content; present multifaceted and dynamic portrayals of physics data, support learner-driven interactions with phenomena, and learning of physics content (Honey & Kanter, 2013; USDOE, 2016).
Playground Physics leverages children’s play, playfulness, and embodied experiences to support their learning of hard-to-teach physics concepts. Play and playfulness are compelling frames and strategies through which children explore and notice the world around them (Bergen, 2009; Singer, Golinkoff & Hirsh-Pasek, 2006). They assist in the innovative combinations of thoughts or actions, which can lead to the facilitation of divergent thinking and production of novel solutions to complex problems (Bateson & Martin, 2013). These types of thinking and practices that play and playfulness instill in children have been found reflected, albeit at a higher degree of magnitude, in how scientists approach complex scientific problems. For example, physicists often use playful language (i.e., the dance between ordinary and scientific words) (Mehta, 2002) and construction play (i.e., models) to describe scientific phenomena. Playful thinking has been found to influence important discoveries in biology (Bergen, 2009) and engineering (Resnick, 2004). Playground Physics infuses play and playfulness as embodied mnemonic devices into physics learning, that is, aims to anchor students’ learning by tapping into their exposure to familiar embodied experiences during play (Hackett, MacRae & Holmes, 2020) and intrinsic motivation to play (Domenico & Ryan, 2017). The activities described in detail below focus on helping teachers assist students in making sense of their own physical play activities; and aim to increase students’ motivation to learn physics, improving their physics content knowledge.
What is it and how does it work?
Playground Physics is an instructional program comprising an application [app] and supplemental curriculum designed to support middle school students’ learning of physics concepts: motion, energy, and force. The features of the Playground Physics app include video recording of full-bodied physical play activities (e.g., running, swinging, sliding); selecting one body part (e.g., head, leg, hand, foot) or moving object (e.g., ball, car) and placing dots (i.e., data points) to trace the path of the object or person on the screen through each frame of the video; entering required calibration information (e.g., mass, height and size) about the object or person on the screen; and saving the video. The app uses the information entered and saved (i.e., video of play performance, size, mass) to generate graphs of the play performance, distance traveled, speed, and direction as based either on the motion, force (pull, push), or kinetic and potential energy. The video and graphs are linked, so that users can see the graphs unfolding as the video of their movement is playing, allowing students “…the ability to talk about referents and the symbols which reference them simultaneously in one consistent space using talk, gesture, and representations without distinguishing between them” (Enyedy et al., 2012, p. 352). They can control how fast or slow they want to move through the video by moving a finger along the scrubber at the bottom of the screen and thus pause to examine particular points in the videos and on the graphs.
Users can play and replay the same video via the motion, energy, or force lens. Users can pinpoint with accuracy the physical and scientific phenomenon that is taking place in their everyday play performances. They can see where they are moving the fastest or highest, where a force is pushing or pulling, and where their kinetic and potential energy are at their highest and lowest points. In the motion lens, students can see how distance, speed, and direction changes when the person or object they have recorded moves. In the force lens, students can identify force pairs in the performance. In the energy lens, students can explore a person or object’s potential and kinetic energy. Each lens has stickers that students can place in the path of motion. The stickers in each lens add special effects to the video, helping students better notice and pinpoint the science that is taking place in their play performances. Some stickers show a dust trail to indicate speeding up, while others show an expanding boom where a push force occurs. Users can add stickers to visually illustrate speeding up or where a push force occurs as they play back and forth their videos.
The app is accompanied by a six-week supplemental curriculum (including a student workbook section) to support teachers’ implementation of the program on school playgrounds and classrooms. The curriculum begins on the school playground, where students use the app to video-record their selected physical play activities: running, jumping, sliding, etc. Back in the classroom, the teacher first engages students in sharing and discussing their felt embodied play experiences without referencing the app, then moves to investigating their embodied performances using the videos in the app through the motion, force, and energy lens. Students compare their felt embodied play experiences against the data provided by the app about how fast or slow they were going, how high they were able to swing, etc. The curriculum and app blends embodied physical and virtual activities in playful ways to support students’ reasoning and discussion of their experiences through the lenses of motion, energy, and force.
The curriculum is available for free on the NYSCI’s website and can be accessed at https://noticing.nysci.org/apps/playground-physics/. The iPad app is available for free in the Apple App Store and can be accessed https://apps.apple.com/us/app/playground-physics/id947124790. The Chromebook Extension is available for free Chrome Web Store and can be accessed https://chrome.google.com/webstore/detail/playground-physics/hmapcaddgcoaeopigmicjakdhcodhghf?hl=en-US. The research and development of the program, which started in 2012, has been widely disseminated (Ba, 2017, Ba, 2015; Friedman, Margolin, Swanlund, Dhillon & Liu, 2017; Kanter, Honwad, Diones & Fernandez, 2013; Margolin, Ba, Friedman, Swanlund, Dhillon & Liu, 2020). It is currently being studied in an expansion initiative across New York State (see https://nysci.org/playground-physics/).
The implementation of Playground Physics materials can be grouped into two interrelated groups of activities. The first group of activities—mostly student-driven—is embodied and implemented on a playground. The second group of activities is mostly teacher-driven and happens in the classroom. It is designed to support students’ deep understanding of physics content using the data collected through the app; students’ discussions of their embodied experiences in relationship to the concepts of motion, energy, and force; and explicit scaffolding strategies available in the curriculum. The task-initiation phase in Playground Physics is focused on the first group of activities and less on the second group of activities, which deal with sense-making of formal academic symbols through a heavy reliance on mediated tools and the teacher’s facilitation.
How does the task-initiation process work in Playground Physics?
The goal of the task-initiation process in Playground Physics is to centralize student agency in the learning process of science (Podolefsky, Moore & Perkins, 2013), make visible their rich set of intuitions about the concepts of motion, force, and energy through their physical play performances, and offer students opportunities to reflect and question those intuitions (Enyedy et al., 2012). The task-initiation process is designed to support students in generating their own questions about their play performances and work collaboratively in small groups to make sense of their embodied experiences before dealing with the formal learning of physics content. In the task-initiation phase, students have ownership over how to enact most of the playground activities: (1) select the free or curriculum-suggested physical play performance they want to engage in and movement-problems they want to solve; (2) decide which body-part or object they want to track and explore in their play performance displayed in the app; (3) engage in reconciling their intuitions and embodied experiences to explain what is going on in the app; and (4) determine the degree to which they want to optimize their physical play performances and videos. Examples of how this might unfold are elaborated on below.
Performing embodied play on the playground.

Play…
This first step is physical and action-oriented in nature. Learners define and shape their tasks and questions. It leverages children’s instincts to engage playfully with things they find compelling, like running, jumping, swinging, and sliding. For example, students’ self-generated movement questions can include where I was going fastest and slowest, where I felt a push or a pull, and how much energy I or the object generated at given points.
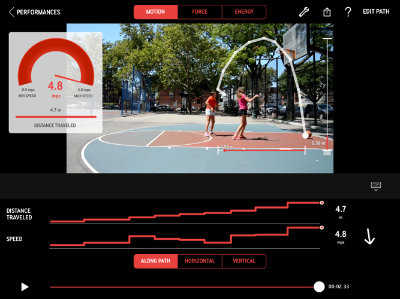
For example, the two girls in the video shown in Figure 3 – taken with the Playground Physics app—are playfully taking turns and not interfering with each other to try for a foul shot on a basketball court. Each girl aims to get the ball into the basket. The video shows how they are using their bodies, the ball, and basketball equipment in different ways to try to achieve their goal.
Experimenting with tracking embodied performances.

Play…
Students receive feedback on their play performance from the Playground Physics app in the form of visuals and quantifications, which are technologically mediated and delayed. That is, students need to get off the playground equipment (e.g., swing, slide) and track their play performances in the app. To start reviewing their embodied play performances in the basketball example, the two girls have to first decide what to track in the video in order to tell the app what matters to them and what they want it to measure in relationship to the targeted goal (i.e., put the ball in the basket). Second, they have to compare the slope of the ball’s path by tracing the ball. They can also focus on their bodies by tracing their height, how they hold their arms or elbows, how far they are from the basket, etc., (see Figure 4). Some of these measurements will make sense, whereas others won’t explain why one ball goes into the basket and the other one does not. The point is not that the app guides them through an appropriate process, but that it provides inquiry tools to consider different ways of looking closely at their own embodied play performance.
The opportunity to scrub back and forth across the video of a performance and to consider what changes in the graphic representation of the physical movement between tracking points opens the question of what constitutes relevant data. If you track too loosely, you may miss the relevant data (that the ball bounces off the backboard). Does it matter whether you track by putting points on the screen at regular intervals (i.e., every other click on the move-forward icon) or just when you see something significant happening, like when the ball is changing direction? These are issues students have to work out by experimenting with different approaches to tracking the movements.
Enlarge…
Reconciliation
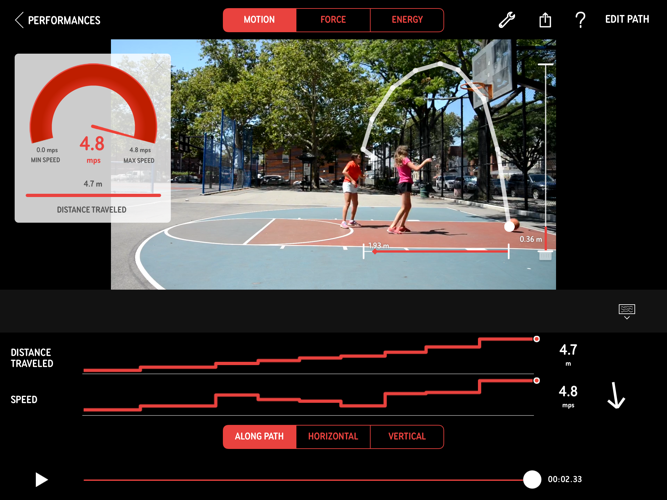
This step which occurs when the students are off the playground equipment is focused on how students attempt to reconcile their prior understanding of the concepts of motion, energy, and force against both their felt embodied experiences and virtually tracked embodied performances, including speed, distance, direction, height, size, and graphs (see Figure 6). For example, while playing on the basketball court, the player may have believed using their visual perception that the ball was going fastest as it started to reach the highest point in their path of motion. However, the graph in the app is showing them that the ball is moving the fastest when it is leaving their hands and again when it is coming down toward the ground, and slower at the apex of the ball’s motion.
Optimizing physical play performances and videos
The information gathered and questions raised from the steps above are designed to lead students to consider “what kinds of movements are optimal for learning and reasoning” (Lindgren, 2015, p. 49). In the case of Playground Physics, this step involves students optimizing their embodied physical performances and addressing how to capture via video physical experiences optimized for physics learning. There is potential for the ways the students move in their live play performance to not be optimal and/or the video to distort the available measurements. In the basketball videos, for example, this step gives students the opportunity to experiment with different performances by shooting the ball from different angles and considering different options about how to best get the ball into the basket. One option is to curve the ball so that it goes directly into the basket and the other is to hit the backboard at an angle that results in the ball going into the basket. This step can be repeated until they feel that they have optimized both their play performances and videos in ways that they believe will be best conducive to addressing their initial questions, for example, “How high can I swing without falling?”, “How fast was I going?”, “How slow was I going?”, “Where did I feel a push or a pull?”, and “How much energy can I generate during my play performances?”
Through the task-initiation process, students test and re-test their play performances and videos in order to answer their own action-oriented questions about what aspects of their play performances make a difference in the process of physics learning. Further, as they engage in this initial comparison-and-verification data-analysis process, the task-initiation phase supports students’ ability to make visible and reflect critically on their rich physics intuitions in relationship to how they felt during their play performances vis-à-vis what the app is telling them happened in terms of physics quantities (e.g., speed, distance). Questions and discoveries about these relationships during the task-initiation phase are a mix of embodied intuitions and data and can be a fertile ground on which to further explore them systematically in Playground Physics’ second groups of teacher-driven activities.
A Spectrum of Task-Initiation Design Principles and Tradeoffs
View table…
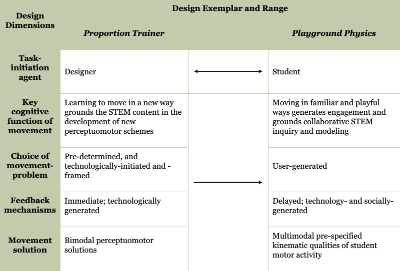
The task-initiation of the two programs reviewed in this article presents both similarities and differences in how they approach and design for embodied math and physics learning (see Table 1). They share the same theoretical design approach – embodied design – that looks to ground STEM content learning in movement problems and tasks, and follow the same design strategies in determining embodied learning goals and tasks, introducing mediating resources, and facilitating how learners negotiate and reconcile their playful embodied experiences as they address their initial movement problems. Despite these similarities, however, the two programs differ in who (the designer or the student) gets to decide what movements to enact and how these environments accommodate student choice during task-initiation. For this theoretical paper, we have deliberately examined two antipodes of this dimensional spectrum – “designer” vs. “student” – in an attempt to surface the contexts and rationales leading to these subtly differentiated design decisions.
|
Design Dimensions |
Design Exemplar and Range |
||
|---|---|---|---|
|
Proportion Trainer |
Playground Physics |
||
|
Task-initiation agent |
Designer | (Double-ended arrow) | Student |
|
Key cognitive function of movement |
Learning to move in a new way grounds the STEM content in the development of new perceptuomotor schemes |
(Right-pointing arrow) |
Moving in familiar and playful ways generates engagement and grounds collaborative STEM inquiry and modeling |
|
Choice of movement-problem |
Pre-determined, and technologically-initiated and -framed |
User-generated |
|
|
Feedback mechanisms |
Immediate; technologically generated |
Delayed; technology- and socially-generated |
|
|
Movement solution |
Bimodal perceptuomotor solutions |
Multimodal pre-specified kinematic qualities of student motor activity |
|
On one end of the task-initiation design spectrum, students’ tasks are heavily guided by the designers. The design principles of the Proportion Trainer require: (1) specific, pre-determined, and technology-framed and -initiated movement-problems; (2) immediate online feedback; and (3) accommodations for a set of bimodal pre-specified perceptuomotor solutions to the movement problem.
Whereas the Proportion Trainer activity is intransigent with respect to task-initiation and movement problem, clinical and eye-tracking measures reveal that within these rigid task-constraints the students develop a vast variety of idiosyncratic sensorimotor schemes by which to discover and enact the movement form (Abrahamson & Abdu, 2020). This finding agrees with the ecological-dynamics framework of constraints-based sports pedagogy (Chow, Davids, Button & Renshaw, 2016) and supports coordination-dynamics analyses of individual pathways toward effecting the neuromuscular realization of a goal movement (Kostrubiec, Zanone, Fuchs & Kelso, 2012).
As such, it would appear that denying students task-choice does not deny them individualizing their learning path. The Proportion Trainer, as a field of promoted action, is designed to entrain students into performing a specific movement form of cultural value, much as one would teach a person a pottery technique, a cello bowing method, or a martial-arts kata (Abrahamson, 2020). What we do not know, however, is whether constraining task-choice in any way compromises students’ motivation to participate in the activity; whether, in contrast, tailoring the activity so as to legitimize task-choice could potentially accommodate a greater diversity of interests; and whether it might thus better foster students’ agency in pursuing their line of inquiry.
On the other end of the task-initiation design spectrum, students are able to define their own tasks and make their own choices about how they engage with the resources available to them. The design principles of Playground Physics require: (1) specific, user-generated movement problems; (2) delayed, hybrid feedback that is both technologically- and socially-generated; and (3) accommodations for a set of multimodal pre-specified kinematic qualities of student motor activity. This informal learning approach privileges students’ agency and playful embodied performances.
This student-directed, low-stakes approach to introducing challenging physics concepts encourages learners to take on new responsibilities and positions vis-à-vis specific scientific ideas (Bevan, Bell, Stevens & Razfar, 2013). While teachers frame and set up the learning environment in this phase by suggesting potential play activities as examples, students are encouraged to engage in specific movement-problem of interest to them. This openness of the task-initiation allows learners to select the types of play performances they want to engage in, ask questions about their own self-generated movement, decide how to explore the environment, and refilm their play performances and videos based on feedback from their peers and teacher as well as from the Playground Physics’ app. As producers and creators, students are immersed in their self-directed and familiar actions on the playground. As learners, they are focused on determining what aspect of their play performances they would like to explore in depth in relationship to the concept of motion, force, or energy, and generating questions about the disconnect between their physical play performances and prior physics knowledge about these concepts. Leveraging their intrinsic motivation to play and their questions about their play performances, learners are able to focus specifically on a movement-problem to investigate. Their playful embodied experiences and own questions ground and prep them for the learning of abstract physics concepts. This open task-initiation gives learners a greater sense of control over the way their interests and questions work together to enhance their learning. To a certain extent, open task-initiation lets students determine how they interact with physics content.
The openness of the task-initiation design process can present time management challenges regarding allowing open-ended play performances and capturing optimally cued performances on the playground for science learning. This step requires allocating enough time for embodied explorations and investigations, as teachers deal with logistical supports, such as organizing students into groups, bringing additional play materials (e.g., balls, jump ropes), letting students play different roles (e.g., performer, recorder, producer), ensuring they get to and back from the playground in an orderly fashion, and monitoring and documenting explanations and discussions on the playground. The Playground Physics curriculum provides guidance on the general management of this process.
Finally, teachers play a central role in making both of these kinds of design choices powerful and effective. Understanding how to make these task-initiation approaches accessible and sustainable for teachers is an additional research direction to engage over time.
This article attempted to bring the dimension of task-initiation to the community’s attention by juxtaposing two embodied-design programs that differ with respect to the designers’ decisions for task-initiation. In deciding to what degree one should grant students agency in task-initiation, educational designers draw on their pedagogical philosophy, learning theory, heuristic design frameworks, and available technologies. This decision appears to bear on both students’ engagement and learning outcomes. Future research taking on this question would ideally employ comparison methodology that holds all other factors equal. For us, the co-authors, this dialogue has been important in surfacing our respective implicit assumptions, considerations, and objectives, which turned out to be overlapping in parts and dramatically different in other respects. We believe that the best of our design worlds can be combined, in the service of STEM engagement and learning. We look forward to engaging with the educational-design community to understand tradeoffs of design decisions with respect to task-initiation.
References
Abrahamson, D. (2012). Discovery reconceived: Product before process. For the Learning of Mathematics, 32(1), 8-15. https://www.jstor.org/stable/23391944
Abrahamson, D. (2020). What you feel Is what you get: Understanding metaphor as sensorimotor dynamics. The Senses and Society, 15(2), 216–238. https://doi.org/10.1080/17458927.2020.1764742
Abrahamson, D. (2019). A new world: Educational research on the sensorimotor roots of mathematical reasoning. In A. Shvarts (Ed.), Proceedings of the annual meeting of the Russian chapter of the International Group for the Psychology of Mathematics Education (PME) & Yandex (pp. 48–68). Yandex.
Abrahamson, D. & Abdu, R. (2020). Towards an ecological-dynamics design framework for embodied-interaction conceptual learning: The case of dynamic mathematics environments. In T. J. Kopcha, K. D. Valentine & C. Ocak (Eds.), Embodied cognition and technology for learning [Special issue]. Educational Technology Research and Development. https://doi.org/10.1007/s11423-020-09805-1
Abrahamson, D. & Bakker, A. (2016). Making sense of movement in embodied design for mathematics learning. Cognitive Research: Principles and Implications, 1(33).
Abrahamson, D. & Lindgren, R. W. (2014). Embodiment and embodied design. In The Cambridge handbook of the learning sciences (2nd ed., pp. 358–376). Cambridge University Press.
Abrahamson, D., Nathan, M. J., Williams–Pierce, C., Walkington, C., Ottmar, E. R., Soto, H. & Alibali, M. W. (2020). The future of embodied design for mathematics teaching and learning. Frontiers in Education, 5(147). https://doi.org/10.3389/feduc.2020.00147
Ba, H. (2017). Spotlight: New York Hall of Science Playground Physics. Unpublished manuscript submitted to the U.S. Department of Education’s Investing in Innovation Fund.
Ba, H. (2015). Lessons Learned from Playground Physics: A digital noticing tool designed to support science affect and learning. Unpublished manuscript presented at the U.S. Department of Education’s Investing in Innovation Fund’s Annual Director Meeting, Washington, DC., June 9-12.
Bateson, P. & Martin, P. (2013). Play, Playfulness, Creativity and Innovation. New York: Cambridge University Press.
Bergen, D. (2009). Play as the learning medium for future scientists, mathematicians, and engineers. American Journal of Play, 1(4), 413–428.
Bevan, B., Bell, P., Stevens, R. & Razfar, A. (Eds.). (2013). LOST Opportunities: Learning in out-of-school time. New York, NY: Springer.
Britner, S. L. & Pajares, F. (2006). Sources of science self-efficacy beliefs of middle school students. Journal of Research in Science Teaching, 43(5), 485-499. https://doi.org/10.1002/tea.20131
Chow, J. Y., Davids, K., Button, C. & Renshaw, I. (2016). Nonlinear pedagogy in skill acquisition: An introduction. Routledge.
Danish, J. A., Humburg, M., Tu, X., Davis, B. & Georgen, C. (2018). Modeling bees by acting as bees in a mixed reality simulation. Paper presented at the International Conference of the Learning Sciences, London, England. In J. Kay & R. Luckin (Eds.), “Rethinking learning in the digital age: Making the Learning Sciences count,” Proceedings of the 13th International Conference of the Learning Sciences (ICLS 2018) (Vol. 2, pp. 1276–1278). International Society of the Learning Sciences.
DeSutter, D. & Stieff, M. (2017). Teaching students to think spatially through embodied actions: Design principles for learning environments in science, technology, engineering, and mathematics. Cognitive Research: Principles and Implications, 2(1), 22. https://doi.org/10.1186/s41235-016-0039-y
Domenico, S. I. & Ryan, R. M. (2017). The emerging neuroscience of intrinsic motivation: A self-determination research. Frontiers in Human Neuroscience, 11(145), pp. 1-14. https://doi.org/10.3389/fnhum.2017.00145
Enyedy, N., Danish, J. A. & DeLiema, D. (2015). Constructing liminal blends in a collaborative augmented-reality learning environment. International Journal of Computer Supported Collaborative Learning, 10(1), 7-34. https://doi.org/10.1007/s11412-015-9207-1
Enyedy, N., Danish, J. A., Delacruz, G. & Kumar, M. (2012). Learning physics through play in an augmented reality environment. International Journal of Computer-Supported Collaborative Learning, 7(3), 347–-377. https://doi.org/10.1007/s11412-012-9150-3
Fine, S. M. (2014). “A slow revolution”: Toward a theory of intellectual playfulness in high school classrooms. Harvard Educational Review, 84(1), 1–23. https://doi.org/10.17763/haer.84.1.qtr193464843n334
Flood, V. J. (2018). Multimodal revoicing as an interactional mechanism for connecting scientific and everyday concepts. Human Development, 61(3), 145–173. https://doi.org/10.1159/000488693
Friedman, L.B., Margolin, J., Swanlund, A., Dhillon, S. & Liu, F. (2017). Playground Physics Impact Study. American Institutes for Research. Available from www.air.org/playgroundphysics.
Fugate, J. M. B., Macrine, S. L. & Cipriano, C. (2019). The role of embodied cognition for transforming learning. International Journal of School & Educational Psychology, 7(4), 274-288. https://doi.org/10.1080/21683603.2018.1443856
Gigerenzer, G. & Brighton, H. (2009). Homo heuristicus: Why biased minds make better inferences. Topics in Cognitive Science, 1(1), 107-144. https://doi.org/10.1111/j.1756-8765.2008.01006.x
Hackett, A., Holmes, R. & MacRae, C. (2020). Introduction to part II. Museum spaces. In Abigail Hackett, Christina MacRae & Rachel Holmes (eds.). Working with Young Children in Museums: Weaving theory and practice, (p. 9). New York, NY: Routledge.
Honey, M. & Kanter, D. E. (2013). Design, Make, Play: Growing the next generation of STEM innovators. New York, NY: Routledge.
Jewitt, C., Price, S. & Sedo, A. X. (2017). Conceptualising and researching the body in digital contexts: Towards new methodological conversations across the arts and social sciences. Qualitative Research, 17(1), 37-53. https://doi.org/10.1177/1468794116656036
Kanter, D. E., Honwad, S., Diones, R. & Fernandez, A. (2013). SciGames: Guided play games that enhance both student engagement and science learning in tandem. In M. Honey & D. E. Kanter (Eds.), Design, make, play: Growing the next generation of STEM innovators, (pp. 182–197). New York, NY: Routledge.
Kostrubiec, V., Zanone, P.-G., Fuchs, A. & Kelso, J. A. S. (2012). Beyond the blank slate: Routes to learning new coordination patterns depend on the intrinsic dynamics of the learner -- experimental evidence and theoretical model [Hypothesis & Theory]. Frontiers in Human Neuroscience, 6. https://doi.org/10.3389/fnhum.2012.00222
Lee, V. R. (Ed.) (2015). Learning Technologies and the Body: Integration and implementation in formal and informal learning environments. New York, NY: Routledge.
Lindgren, R. (2015). Getting into the cue: Embracing technology-facilitated body movements as a starting point for learning. In Victor R. Lee (Ed.), Learning technologies and the body: Integration and implementation in formal and informal learning environments (pp. 39–54). New York, NY: Routledge.
Mehta, A. (2002). The playful language of math. Unpublished manuscript. Duke University. Available from www.duke.edu/~acm17/mehta.w2.pdf.
Margolin, J., Ba, H., Friedman, L., Swanlund, A., Dhillon, G. & Liu, F. (2020). Examining the Impact of a Play-Based Middle School Physics Program. Journal of Research on Technology in Education, 53(2), 125-139, https://doi.org/10.1080/15391523.2020.1754973
Podolefsky, N. S., Moore, E. B. & Perkins, K. K. (2013). Implicit scaffolding in interactive simulations: Design strategies to support multiple educational goals. Retrieved at http://arxiv.org/abs/1306.6544
Pouw, W. T. J. L., van Gog, T. & Paas, F. (2014). An embedded and embodied cognition review of instructional manipulatives. Educational Psychology Review, 26(1), 51–72. https://doi.org/10.1007/s10648-014-9255-5
Resnick, M. (2004). Edutainment? No Thanks. I prefer playful learning. Associazione Civita, 14, 1–4.
Russell, J. L., Kehoe, S. & Crowley, K. (2017). Linking In-School and Out-Of-School Learning. In Kylie Peppler (Ed.), The SAGE Encyclopedia of Out-Of-School Learning, (pp. 445–-449). Los Angeles, CA: SAGE reference.
Shvarts, A. & Abrahamson, D. (2019). Dual-eye-tracking Vygotsky: A microgenetic account of a teaching/learning collaboration in an embodied-interaction technological tutorial for mathematics. Learning, Culture and Social Interaction, 22, 100316. https://doi.org/10.1016/j.lcsi.2019.05.003
Singer, D.G., Golinkoff, R.M. & Hirsh-Pasek, K. (Eds.) (2006). Play=Learning: How play motivates and enhances children’s cognitive and social-emotional growth. New York: Oxford University Press.
Skulmowski, A. & Rey, G. D. (2018). Embodied learning: introducing a taxonomy based on bodily engagement and task integration. Cognitive Research: Principles and Implications, 3(1), 6. https://doi.org/10.1186/s41235-018-0092-9
Tran, C., Smith, B. & Buschkuehl, M. (2017). Support of mathematical thinking through embodied cognition: Nondigital and digital approaches. Cognitive Research: Principles and Implications, 2(1), 16. https://doi.org/10.1186/s41235-017-0053-8
U.S. Department of Education [USDOE]. (2016). STEM 2026: A vision for innovation in STEM education. Washington, DC: U.S. Department of Education.
Wieman, C. & Perkins, K. (2005). Transforming physics education. Physics Today, 58(11), 36-41.
Zeyer, A., Çetin‐Dindar, A., Md Zain, A. N., Juriševič, M., Devetak, I. & Odermatt, F. (2013). Systemizing: A cross‐cultural constant for motivation to learn science. Journal of Research in Science Teaching, 50(9), 1047–1067. https://doi.org/10.1002/tea.21101
Zohar, R., Bagno, E., Eylon, B. & Abrahamson, D. (2018). Motor skills, creativity, and cognition in learning physics concepts. Functional Neurology, Rehabilitation, and Ergonomics, 7(3), 67–76. https://edrl.berkeley.edu/wp-content/uploads/2019/06/ZoharBagnoEylonAbrahamson.2017.Movement.pdf
