Design for Learning in Uncertain Contexts: Developing a Maths Curriculum Framework for Emergency Situations
a Research Division, Cambridge Assessment, University of Cambridge, UK.
b Cambridge Mathematics, University of Cambridge, UK.
Abstract
In this paper we outline the design process that we used to create a framework of maths content for use in Education in Emergency (EiE) situations. EiE describes contexts where learners are forcibly displaced by civil conflict or environmental disaster. Although these situations require a fast response, they can last for a period of years, and often require the coordinated actions of various non-governmental and charity aid agencies. We describe the development of a series of maths concept sequences that would form the mathematics component of a larger curriculum framework (including literacy and science content). This framework of concepts would be used by educators in emerging EiE situations to help them to plan and organise their curriculum and to coordinate learning resources. Outlining our maths development project, we conceptualise the external and internal constraints that we navigated along the way.
Introduction: Education in Emergencies as a development context
Education in Emergencies (EiE) as a field of study emerged around the turn of the 21st Century. Emergency situations are formally defined as those where ‘man-made or natural disasters destroy, within a short period of time, the usual conditions of life, care and education facilities for children and therefore disrupt, deny, hinder progress or delay the realisation of the right to education’ Committee on the Rights of the Child, 2008). This definition includes a variety of contexts, including cross-border education initiatives where learners are displaced from their original setting (e.g. Thailand/Myanmar, see Ball & Dim, 2016), and situations where learners do not cross any borders but need support in their local setting due to conflict or natural disaster (e.g. Afghanistan, see Dryden-Peterson, 2011).
The contemporary scale of emergency human displacement is considerable, and the significant complications around the issue make it imperative that efforts are made to help to remediate the effects of the situation on learners. For example, in 2019 there were an estimated 71 million people who were forcibly displaced by conflict, violence, and/or persecution. Of the estimated 26 million refugees who are covered in these displacement statistics, around half were under the age of 18 (United Nations High Commissioner for Refugees (UNHCR, 2019). Although it is recognised that data around displacement is complex to gather and interpret, it is calculated that the mean duration of displacement ranges somewhere between 10 and 15 years (Devictor, 2019), which highlights that emergency can be a relatively permanent situation for many displaced people. Moreover, up to 85 percent of those forcibly displaced are hosted by low- and middle-income countries, which puts a strain on host communities and resources (European Commission, 2019), and raises concerns about how integration may be afforded between host and displaced communities.
Establishing an educational response and mobilising resources in an emergency situation is a recognised challenge. The United Nations Children’s Fund (UNICEF) has privileged access to emergency situations, often having a coordinating role for multiple charity and non-governmental agencies who are also present in such a response. Examples of these would include joint working projects with charities such as the Education Above All/Educate a Child Program in Sudan, or various faith-based organizations across a variety of development projects around the globe (see UNICEF, 2003, 2019).
The Learning Passport Curriculum Framework
To support this coordination activity, UNICEF identified the need for the development of a curriculum framework for the primary education phase which could be used in newly emerging emergency contexts. Termed ‘The Learning Passport’, a single framework would guard against the continual development of new learning programmes at the onset of each new emergency, would inform educators’ curriculum planning and learning resource gathering, and free up human resources. This reflects established observations on EiE which note that ‘clearly, each situation is unique, and local communities are best placed to understand the distinctive local needs; but the work of international agencies will be more efficient if they can adopt a common approach to all emergency situations’ (Halstead & Affouneh, 2006, p. 203).
Researchers at Cambridge Assessment and Cambridge Maths, two departments of the University of Cambridge, worked on the development of the curriculum framework. At this stage it is important to outline our concept of a curriculum framework. For us, a curriculum framework is a document containing a clear statement of concept sequences that represent learning progressions in specific subjects (in this case, literacy, maths, and science). These sequences would then be used as a foundational reference point for the development of specific learning programmes by educators, such as consultants working with international aid projects, in the different learning contexts who would adapt, expand, and integrate additional elements to the framework.

https://www.cambridge.org/files/7615/8465/3386/The_Curriculum_Framework-Maths_Science_Literacy.pdf
Our framework would outline essential development of a restricted but vital set of core concepts, principles, fundamental operations, and knowledge. For the mathematics part of the curriculum framework the descriptors would be organised into domains and then into a sequence of up to 12, non-age defined levels. Pages 36-66 of the developed framework (Cambridge Assessment, 2020) show the learning progressions that we developed for maths.
This focus may appear reductivist, but by fixing on essential concepts the framework would provide an essential foundation which can be further elaborated and supplemented if needed. In this way, the framework allows flexibility for educators to make locally relevant decisions around how to introduce and bring to life these common concepts through their teaching. It also allows space for educators to include additional learning elements that are of contextual significance to the learning programmes in the different displacement localities (e.g. the need to have space for culturally specific content such as peace building in civil conflict zones, or on specific health initiatives in spaces affected by environmental emergency).
Once developed, the framework of concept sequences would be available for implementation and piloting in an emergency context, which would be coordinated by UNICEF. The location of this implementation was not known to the development team in Cambridge at the time of the development. To support local and regional education sectors in this contextualisation process we also developed adaptation guidance in the form of ‘contextualisation principles’ for consideration when developing the framework into a complete and deliverable curriculum (Cambridge University, Cambridge University Press & Cambridge Assessment, 2020).
In the rest of this paper we describe a process that we devised for developing the sequences of maths concepts that could form the basis for a learning programme aimed at refugee and displaced learners.
Constraints on the Framework Design Process
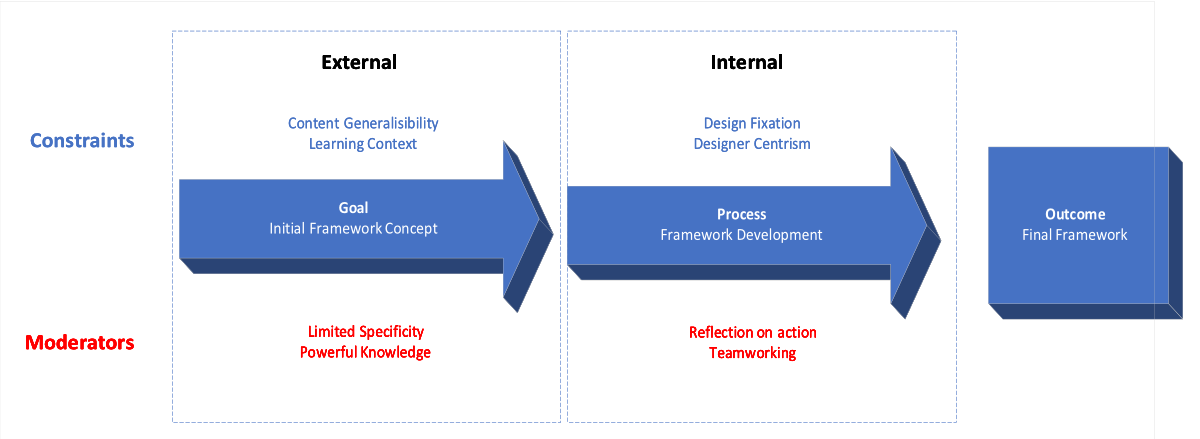
Considering our framework development process from a design perspective, the uncertainty of the emergency education context represents a set of constraints that influence decision making during the development process. Constraints are a fundamental element of decision making in a design process (Bradley, 2015). According to Reitman (1965) the interplay of constraints helps to define a problem. We argue, in line with Simon, that the constraints attached to the emergency development context mean that our development has the characteristics of an ill-structured problem, since one indicator of an ill-structured problem is the ‘lack of a set of terms for describing or characterising the initial state’ (Simon, 1973, p. 183).
As part of the reflection on how we developed the sequence of maths concepts as part of the curriculum framework, we conceptualise this process around two problems; the first managing external constraints and the second managing internal constraints.
External design constraints
External design constraints include the contextual elements that influence framework design and content. These design constraints (which are external because the developers have no control over them) are areas of information with low specificity that contribute to heightened levels of designer uncertainty.
EiE is a very broad field (both metaphorically and physically) which conveys limited information about any specific emergency situation. This limited information relates to areas such as learner abilities (including any social and emotional characteristics), and their aspirations beyond their immediate circumstances. There are also information limitations around the specific availability of learning resources, about learning facilitator characteristics (or if such facilitators exist in all contexts), and around the nature of the learning spaces that are available to learners.
For our maths concept sequence development, this lack of specificity manifested itself in insecurities about what learning content should be included to meet the needs of the learners covered by the design brief. As a foundation for expanding the mathematical content of the framework, we needed to consider the balance of two elements. We needed to recognise the limitations of the evidence about the learning contexts in which the framework would potentially be enacted. This recognition would be mediated through discussions with UNICEF and other NGO sources, and through our involvement in a selection of field visits to refugee camp contexts. We also needed to consider the appropriate mathematical content that would be most relevant to these learning contexts.
As our intention was to create a framework that could apply across different EiE contexts, we needed to think about the limits of knowledge generalisation, as we didn’t want to structure our framework around content that had limited applicability. Generalisation links with how knowledge relates to a variety of contexts and as part of this we engaged with emerging debates in the field of sociology of education around Powerful Knowledge (PK).
Mirroring the distinction between spontaneous and non-spontaneous concepts (e.g. Vygotsky, 1986), PK involves knowledge that has a predictive and explanatory capacity that can take learners ‘beyond their own experiences’ (Young, Lambert, Roberts & Roberts, 2014, p. 7). Such knowledge is a specialised form of knowledge that is recognised by experts as being a reliable explanation of the world through its systematic organisation of the relationship of concepts (Young, Counsell, Burn & Chapman, 2016) – including the sequencing of concepts (Young, 2013).
This means it falls within disciplines, with mathematical knowledge being distinct from, say, sociological knowledge, and having its own organising concepts and logic. For example, Maton (2014) notes the concept of 1:1 correspondence can underpin counting, grouping, sharing, and so has a high explanatory potential across an array of phenomena. In this way the concept has transformative potential, with the learner not seeing the world the same way once this understanding is developed. Essentially, this knowledge allows learners to see the world beyond their immediate experience and context, and because it is built up over time by accumulated systematic observation in a community of subject experts, it differs from the context-based, everyday knowledge that younger learners may construct without intervention. Since we were focusing on EiE situations where learners were highly likely to have limited time available for formal learning, we wanted to identify the most important knowledge with the best explanatory value that could be covered in this limited learning space.
This point links to a second, and important element of PK theory, which is the separation between curriculum and pedagogy (Young, 2013), and recognition of the important role of the educator in learner development. PK has a narrow definition of the curriculum (the knowledge that learners are entitled to know [Young, 2013, p. 111]), but it also recognises that learner experiences are a crucial resource for both learner and teacher. Pedagogy (as distinct from curriculum) needs to consider content selection, pace, and coherence across knowledge in relation to a teacher’s understanding of the capabilities, experience and potential of the learner. In other words, teachers need to relate curriculum content to the experience and ideas of the learners.
There continue to be debates about the influence of discipline-based knowledge on reinforcing traditional learning relationships and minimising social transformation. For example, shifts in thinking in the sociology of education over recent decades have argued that discipline-based, knowledge-centric education has served to maintain social inequalities, for example, through locking out participation for some learners (Alderson, 2020). However, the inability of alternative curricular models (e.g. competency or skills-based) to attain large scale social transformation has also led some to suggest that education models that ignore the transformative power of knowledge will struggle to undermine existing socio-economic inequalities (Abadzi, 2006; Sen, 2020; Wheelahan, 2007).
A premise of the PK perspective is that social equity will be enhanced through allowing all learners access to generalisable knowledge that can be used to understand (and transform) their world. By acknowledging that some knowledge is more powerful than other knowledge, it follows that ‘the most fundamental inequality in education is that of access to the best knowledge’ (Moore, 2013, p. 335).
Internal design constraints
In addition to the external design constraints linked to the limited available information around the learning context, there are also a set of constraints which we can have some degree of control over – which we call internal design constraints. These constraints centre on decision making around how to ensure that the developers are confident that the development is progressing towards its aims. The focus of this problem considers the serial nature of design problem solving (Simon, 1973, p. 192) and the ability of the developers to self-regulate the development process so that it attains its outcomes.
When looking at ill-structured design contexts, it is claimed that in-process refinement is a particularly important condition for design brief achievement, and this can involve ‘reflection-on-action’ (Jonassen, 1997; Schön, 1983). It is acknowledged that in ill-structured contexts, which we suggest EiE development contexts can be, a designer is rarely in a position to identify all possible solutions to a task at hand (Seitamaa-Hakkarainen, 2000). However, in practice, designers do reach solutions. It seems that to reach solutions designers engage with the interplay of constraints (Reitman, 1965) and move from a position of uncertainty to one of increasing certainty. Design literature suggests that this movement towards a solution involves refinement during the development process and the countering of two phenomena that may compromise this refinement; fixation and designer-centrism.
Fixation is a block to insight (Crilly, 2015, p. 56) and includes counterproductive effects that lead to the overlooking of novel solutions. Fixation can be caused by developers’ prior knowledge, resistance to novel practices, and targeted focusing that is overly narrow. A developer’s prior knowledge, including their heuristic ways of working, can lead to what are considered to be efficient behaviours that often follow a path of least resistance and which can overlook other potential design pathways (Hatchuel, Le & Weil, 2011). Intentional resistance to change can also be a block to developer reflection-on-action (Deserti & Rizzo, 2013). This resistance may be based on ideas that traditional design systems are better than novel ones since they offer a workable solution, or on an attachment to outdated beliefs (Youmans & Arciszewski, 2014, p. 121). Finally, a developer’s focus on the immediate design frame can obstruct the seeking of novel solution as the designer attends to narrow objectives and overlooks broader project goals (McKenney, 2019).
Designer-centrism is another potential block to designers’ reflection-on-action. Designer ego involvement in development is recognised (Burgess, 1970; Schunn, 2008), but it is also considered to be a weak basis for anticipating others’ perspectives (Derks & Bakker, 2010). This presents a design problem as a designer’s perspective may contain incorrect assumptions about the user, an issue that has been observed in past studies (e.g. Jirotka, Luff & Heath, 1993). The tying of the design process to a developer’s own ego-system (Zuiker, Piepgrass & Evans, 2017) contributes to an inability for designers to move beyond simplified or essentialized portraits of potential users of a development. These observations help to account for so-called design failures, which include unanticipated alternative uses and misuses of designs (Cascini, Del Frate, Fantoni & Montagna, 2010). The potential problems attached to an over emphasis on the designer perspective reinforces the need for developers to construct as rich a conceptualisation as possible of those most directly influenced by a development (Harper, Bird, Zimmermann & Murphy, 2013).
Literature provides several potential ways of countering fixation and designer-centrism, which we tried to build into our development. Agogué, Poirel, Pineau, Houdé & Cassotti (2014) highlight how cognitive bias based on a designer’s prior experience can be a limiter on their self-reflection. They go on to argue that this experience-based perspective can be augmented using theory to balance the decision-making process. In this way, theory represents a generalising contribution as it brings an external and explanatory influence on the process. Teamwork also potentially reduces the impact of a single designer perspective through bringing multiple perspectives to the design process (Crilly, 2015). Another approach to minimising the singular influence of one designer on the design process is to consider the interconnecting elements of a development and to ensure that there is design coordination (Simon, 1973, p. 191) among the different contributors to the process. This consideration focuses on ensuring that there is cohesion across the design through encouraging consensus and agreement across the stages of development.
Case study: Designing a Maths Framework with Constraints
In this section we outline how we designed the maths concept progressions for the EiE Curriculum Framework by navigating external and internal constraints. Firstly, we describe how we dealt with the external constraints by harnessing the potential of frameworks to coordinate action, and through structuring content choices around the concept of PK. Then we describe how we dealt with the internal constraints by incorporating the theoretical and practical experience of experts alongside effective teamworking.
External constraints: framework and content design
Using a framework as a device for structuring educational activity can afford both centralisation and localisation. A framework that includes parsimoniously chosen, key components of a learning sequence possesses a generic capacity to coordinate the actions of educators and learners as it focuses on high-level learning concepts and sequences between these concepts. Drawing on Kress & van Leeuwen’s (1996) analysis of visual design, the representation of linkages between elements of content in a directed framework is an effective way of authoritatively representing the structure of the system of concepts. A learning framework can provide a centralised sequenced structure of concepts that need to be learned, but it also allows flexibility for localised decision making around how to enact and bring to life these concepts through choosing the specific learning features and activities that should be included in learning programmes in any particular context.
In this way the framework would perform the function of being a Boundary Object between the designers and the potential users of the framework, encouraging localised decision making around common concepts. ‘Boundary Object’ is a term coined by Star & Griesemer (1989) and describes artefacts, such as documents, that are designed by different teams to coordinate their interconnected but remote activities. In the case of this project, these teams included the different subject specialist groups who were articulating the framework content as well as the UNICEF and other NGO teams who were conveying perspectives from across various displacement contexts. A feature of such objects is that they allow space for differential interpretation – recognising that multiple perspectives may exist around a common focus and act as a spur for interaction. For our project these interactions included ongoing, virtual conversations across the teams about the shape of the emerging framework.
Our framework design purposefully focused on a limited number of essential maths concepts, allowing space for localised flexibility to augment this essential foundation if needed. The framework would therefore allow for appropriately variable implementation, meaning that learning facilitators could respond to the specific needs of learners whilst the framework would give a common structure to learning, guide assessment practice, and promote alignment of instruction, materials, and content across multiple emergency contexts.
The foundational and generalising ambition of the framework shaped our choices about the type of mathematical content that should populate the framework. To do this we wanted to consider what the ‘best’ form of knowledge to include would be. Our choice was influenced by discussions about PK (discussed earlier). According to Young (2013), ‘in all fields of enquiry, there is better knowledge, more reliable knowledge, knowledge nearer to truth about the world we live in’ (Young, 2013, p. 107). Young (2013, 2014) outlines how PK is predictive, explanatory and enables the visualising of alternatives, employing concepts that can illuminate understanding beyond the immediate culture of locally produced knowledge. This means that, with appropriate pedagogic input, learners can think about concepts that they may not encounter in their everyday experience. This focus on PK informed the way that we engaged with the internal constraints of the design challenge, which we outline in the next section.
Internal constraints: theory, practice, and teamworking
As we outlined earlier, internal design constraints include the design elements that the developers had some control over. These constraints cover the degree of designer reflection built into the development process and which influence the attainment of the design brief. Our development involved the integration of expert practice perspectives alongside research literature to reduce the risk of designer-centrism. This was the first element of reflection-on-action that we built into our framework development process. This process was also augmented by extensive teamworking based on the establishment of common ground across the development group, which was the second element of reflection-on-action that we built into our framework development process (and is described in more detail later in this section).
To start to get a sense of the ways that maths is conceptualised and organised across different national contexts we carried out a mapping exercise. This allowed us to explore commonalities in the ways that maths is structured across different educational systems. For example, the consideration of data from across educational systems would allow our development process to be informed by evidence from systems where learners were generally attaining good levels of mathematical performance. There is evidence that attainment has some relationship with curriculum structure, particularly where the arrangement of topics and sequences cohere with a relatively small set of frameworks that align with the underlying structure of a discipline (Fortus, Adams, Krajcik & Reiser, 2015; Schmidt, Wang & McKnight, 2005).
The use of comparative data as a research evidence base for curriculum policy and practice reform is considered to be a useful approach (Burns & Schuller, 2007) since it is argued that there are common characteristics of successful systems (Schmidt, 2004). As a result, this approach has been used to inform curriculum development across a variety of contexts (Creese & Isaacs, 2016; Karseth & Sivesind, 2010; Oates, 2011; Ruddock and Sainsbury 2008).
To identify national systems that were attaining good levels of performance we considered outcomes data from recent international comparisons, including Trends in International Mathematics and Science Study (TIMMS), the Progress in International Reading Literacy Study (PIRLS), the Programme for International Student Assessment (PISA), and The Global Index of Cognitive Skills and Educational Attainment. According to Elliott (2016), High Performing Jurisdictions (HPJs) can be identified as being present in one of the top 20 positions of at least six of the seven of the most recent international comparisons. Our analysis identified nine jurisdictions of interest (Table 1).
| Curriculum | Year | Level/Stage | |
|---|---|---|---|
| Australia | Victoria | 2016 | F - 10A |
| Canada | Alberta | 2016 | K - 9 |
| China | Shanghai | 2011 | 1 - 9 |
| Finland | 2016 | 1 - 9 | |
| Hong Kong | 2017 | K - S6 | |
| Japan | 2008 | 1 - 9 | |
| United States | Massachusetts | 2017 | Pre-K – 12 |
| New Zealand | 2007 | 1 - 13 | |
| Singapore | 2013 | P1 – S4 | |
We analysed all the maths curriculum documents from these HPJs to identify the domains in each. In general, there was a broad consensus around the common domains across the different curricula, with all including Number, Measurement, Geometry, Statistics, and Algebra.
The identification of these domains (and then some further subdomains) allowed us to generate a matrix to collect and compare the sequences. This initial draft was a relatively ‘raw’ matrix that required further interrogation, rearrangement, and validation by subject experts. A small section of the first draft of the matrix is shown in Table 2 (the actual matrix included 35 subdomains and 13 levels). The information gathered from across the HPJs is organised into a series of levels. These levels are not linked to age or school grade but characterise how progression was represented across the sampled curriculum documents for each domain/subdomain. Some sequences included few levels of progression (e.g. ‘measurement/money’), whilst others had up to 13 levels of progression (e.g. ‘number/multiplication’, and ‘measurement/angle’). It is important to note that the levels across the subdomains at this stage of analysis are not aligned with each other (so ‘Level 2 Counting’ is not necessarily equivalent to ‘Level 2 Decimals’).
| Domain | Subdomain | Main concept | Level 1 | Level 2 | Level 3 |
|---|---|---|---|---|---|
| Whole number (+4 operations) | Number system | Odd / even numbers | Negative numbers | … | |
| Naming/ Conserving | 1:1 correspondence; concept of whole numbers | Name numbers < 20 (last number is the name) | … | ||
| Addition | Counting | Objects < 20 | < 100; Forward and backward | … | |
| Fractions & Decimals (+4 operations) | Decimals | Representing quantities < 1 | Decimal system (concrete models) | … | |
| 4 operations | Basic addition / subtraction/ multiplication / division | Multiplication / division by whole numbers and powers of 10 | … | ||
| Fractions | Fractions as parts | Simple fractions; Sharing into groups | Halving/Doubling; Half as two equal parts; Fractions < 1 as part of a whole; Fraction notation | … | |
| Measurement | Length | Direct comparison of length; Estimate / Compare the length / height of objects | Informal / non-standard units (comparison) | … | |
| Time | Direct comparison of time | ‘Seconds’, ‘minutes’, ‘hours’, ‘days’, ‘weeks’, ‘months’, ‘years’ | … |
There are limitations of using curriculum document review as a sole source of evidence for framework development, so it was important to engage with experts and theory to augment these documentary data sources. This dual approach (employing both empirical evidence and theoretical reasoning) has similarities to established approaches that interlink empirical observation and research to optimise curriculum design (e.g. Smith, Wiser, Anderson & Krajcik, 2006).
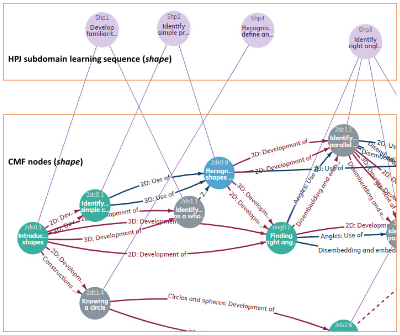
To augment our mapping phase, we collaborated with a team of specialists from Cambridge Maths who, at the time of our framework development, were in the process of developing their own framework of maths concepts (The Cambridge Maths Framework [CMF]). The CMF is a loosely age-related map of the full domain of mathematical knowledge from pre-school to the end of the upper secondary phase of education in the UK and based on progressions in organising concepts and principles. It treats mathematics as a connected web, with mathematical ideas expressed as nodes and relationships between ideas expressed as edges (connections between nodes) (Jameson et al., 2020, p. 7). For more information on the development of CMF see Cambridge Mathematics (2019b).
Enlarge…
Our collaboration with these experts moved through five review stages as we refined our curriculum content framework. These stages are, in outline:
- Extract a subdomain learning sequence from the HPJ learning sequence.
- Relate the HPJ subdomain sequence to nodes in the CMF. These nodes, derived from extensive research literature, indicate the key underpinning concepts that contribute to understanding larger, more expansive concepts.
- Specialist analysis to relate the HPJ learning sequence to the sequence of CMF nodes (see Figure 1).
- Restructure the concept sequences, establish some new sub-domains, and add concepts to these new sub-domains.
- Draft the final concept sequence. This phase involved CMF experts re-writing the statements so that they clearly represented the concepts within them.
For additional information about the visualisation map of the CMF see Cambridge Mathematics (2019a)
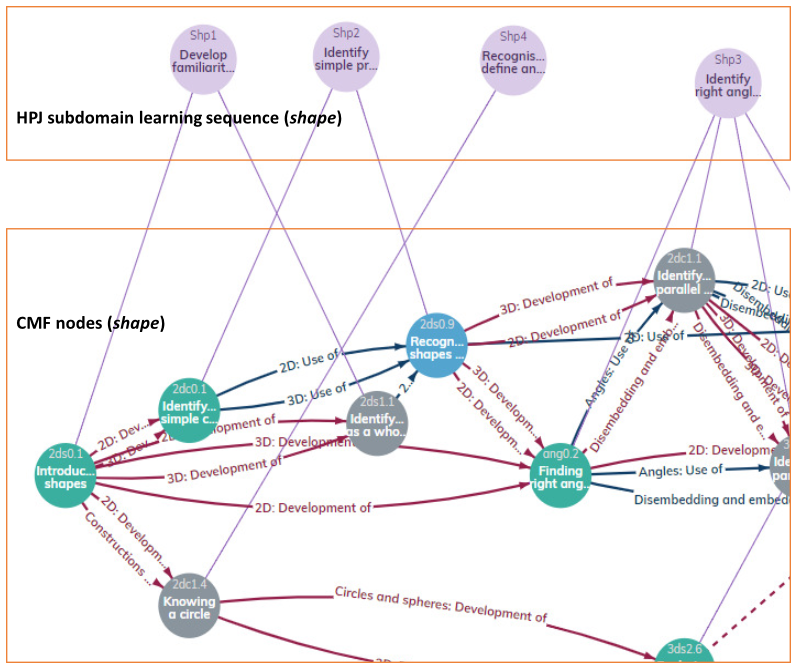
The process of relating the HPJ sequences to the CMF node sequences involved team working, and this was the second element of reflection-on-action that we built into our framework development process. The appeal to distributed expertise inevitably involved the interaction of expert groups, and to facilitate this we needed to establish a strong shared basis of understanding around the aims of the framework development.
The review work with the CMF experts for this development was carried out over a series of 14 meetings and workshops. To establish a firm grounding for the interactions across the expert group (which included specialists from across different domains of maths) we needed to consider how we set the meeting agenda.
The set up for these meetings was informed by our theorisation of establishing common ground amongst the partners. The common ground notion holds that all collective actions are made possible where participants share a common underpinning knowledge on which they can build a joint vision (Clark & Brennan, 1991; Littleton & Mercer, 2013).
To establish common ground, we introduced the subject experts to the key principles that underpinned our framework development process, and to the EiE context. This allowed the experts to orient themselves towards the conditions that learners may face in the EiE contexts where the framework would be enacted. In some cases, this common information allowed the experts to make judgments about which content elements should be included. For example, there were decisions made to prioritise foundational concepts, such as similarity and congruence, rather than specific trigonometric ratios and their applications. It was considered that these concepts would ready learners for later encounters with trigonometry and would be relatively resource agnostic from a teaching perspective.
The meetings grappled with discussions around several framework design elements. These elements included decisions about the number of levels into which these descriptors would be organised, the level of granularity in which the descriptors were described, and the extent of coverage overlaps between the different areas of the emerging framework. An important element of these discussions was the opportunity for the experts to negotiate and share meaning. By establishing an agreed form of words for expressing concepts in the framework the experts established and reinforced their shared vision and explained how they developed a sense of trust in each other. These agreements are an important form of coordination that is considered crucial for successful design (Simon, 1973).
Summary of design process
Developing our maths framework for use in EiE contexts presented us with a design challenge due to the extended distance between the context of the development process and the potential EiE enactment context. Even though field visits were carried out by some of our development team, there were inevitable concerns that there was a lack of relevant information that could be key to informing the development process. This limited information related to areas such as learner abilities, their aspirations beyond their immediate circumstances, limitations around the specific availability of learning resources, facilitators, and learning spaces.
At the same time, there were ethical considerations that we needed to attend to as we attempted to create a new learning framework. Given the anticipated vulnerability of learners in EiE contexts, the design process needed to be built on principled foundations as we could not take design risks that could harm learner outcomes. We conceptualised our approach to this design challenge as being the navigation around two design problems that centred on different sets of constraints (Figure 2).
Click to enlarge…

Our first design problem involved a set of external constraints. These constraints related to the broad context in which the design was situated, and which we had little control over as developers. To address this challenge, we needed to consider the structure and content of our maths framework design. Building on the affordances of a framework as an organising structure we considered the benefits of collating core maths concepts into a series of linear representations that articulate with each other across levels in subdomains. In this way we were capitalising on the semiotic characteristics of frameworks as a representational form. A linear illustration of information is authoritative and so helps to convey a common interpretation of information to multiple readers. This form of control over information representation is useful for EiE situations where multiple agencies tend to coordinate through ‘virtuous swarming’. By organising important mathematical information into a sequential framework, we sought to provide a common touch point around which professionals could interact. In this way, the framework would work as a Boundary Object and give educators in distributed, emergency education sectors a common foundation on which to base their subsequent activities (e.g. curriculum planning and learning resource gathering).
We also needed to determine the framework content, and this involved consideration of what the best knowledge would be for this. The concept of Powerful Knowledge helped to inform this area of our development. This notion prioritised a focus on including only core elements of knowledge. This had the corollary of allowing space for localised activity around the framework, and this complemented the inherent flexibility of the framework as a tool for organising joint activity discussed above.
Our second design problem involved a group of internal constraints on the design process that we had some control over. This problem centred on decision making around how to overcome any potential problems associated with the influence of designer-centrism. To mitigate against any potentially negative effects of designer-centrism we worked to ensure that there was space for reflection built into the design process as decisions were made and continually reviewed about the structure and content of the framework. This reflection-on-action acknowledged the notion that design is serial and cumulative in nature, and that decision-making needs to constantly reference the original aims of the design brief.
To deal with this challenge we tried to ensure that the reasons for incorporating mathematical content considered the theoretical and empirical grounds for its inclusion. The use of curriculum mapping and expert reflection supported this process, encouraging discussion around the ways that maths education was organised and how this related to research literature via the CMF. Incorporating the interplay between theory and practice into the development process also implicated the use of teamwork, which was another key element of reflective action built into the design process. To enable this, we considered how we could establish common ground for the contributors to the development, which for our development involved articulating the aims of the development and a focus on the conditions around EiE contexts in general.
At the time of writing the framework is ready for piloting in EiE contexts that are to be identified by UNICEF. The latest information on this can be found at the Learning Passport website https://www.learningpassport.org/learn-more.
Acknowledgement
Some sections of this article have been published in Chapter 3 of The Learning Passport: Curriculum Framework (Maths, Science, Literacy) (Cambridge Assessment, 2020). Chapter 3 was authored by Martin Johnson. We acknowledge and thank the researchers, consultants and reviewers named in “The Learning Passport” for their input and support to the development project.
References
Abadzi, H. (2006). Efficient learning for the poor: insights from the frontier of cognitive neuroscience. Washington, DC: The World Bank Group. http://documents.worldbank.org/curated/en/438221468134385073/Efficient-learning-for-the-poor-insights-from-the-frontier-of-cognitive-neuroscience
Agogué, M., Poirel, N., Pineau, A., Houdé, O. & Cassotti, M. (2014). The impact of age and training on creativity: A design-theory approach to study fixation effects. Thinking Skills and Creativity, 11, 33–41. https://doi.org/10.1016/j.tsc.2013.10.002
Alderson, P. (2020). Powerful knowledge and the curriculum: Contradictions and dichotomies. British Educational Research Journal, 46(1), 26–43. https://doi.org/10.1002/berj.3570
Ball, J. & Dim, A. (2016). Migrant Learning Centers on the Thai-Myanmar Borderland: Giving New Meaning to “Live and Learn”. Childhood Education, 92(3), 200–209. https://doi.org/10.1080/00094056.2016.1180893
Bradley, S. (2015, April 2). Why Constraints Are A Fundamental Part Of Design. Retrieved 23 January 2020, from Vanseo Design website: https://vanseodesign.com/web-design/constraints-help-design/
Burgess, J. H. (1970). Ego Involvement in the Systems Design Process. Human Factors, 12(1), 7–12. https://doi.org/10.1177/001872087001200102
Burns, T. & Schuller, T. (2007). The evidence agenda. In T. Burns & T. Schuller (Eds.), Evidence in Education: linking research and policy (pp. 15–32). Paris: OECD/CERI. http://www.oecd.org/education/ceri/47435459.pdf
Cambridge Assessment. (2020). The Learning Passport Curriculum Framework: Improving the quality of education for vulnerable children everywhere. Cambridge: Cambridge Assessment. https://www.cambridge.org/files/7615/8465/3386/The_Curriculum_Framework-Maths_Science_Literacy.pdf
Cambridge Mathematics. (2019a). An Update on the Cambridge Mathematics Framework. Cambridge: Cambridge Mathematics. https://www.cambridgemaths.org/Images/cambridge-mathematics-framework.pdf
Cambridge Mathematics. (2019b). Cambridge Mathematics Framework. Cambridge: Cambridge Mathematicshttps://www.cambridgemaths.org/manifesto/framework/
Cambridge University, Cambridge University Press & Cambridge Assessment. (2020). The Learning Passport: Curriculum Framework Adaption guidance. Cambridge UK: Cambridge University Press. Retrieved from Cambridge University Press website: https://www.cambridge.org/files/4415/8465/3367/The_Adaptation_Guidance.pdf
Cascini, G., Del Frate, L., Fantoni, G. & Montagna, F. (2010). Beyond the Design Perspective of Gero’s FBS Framework. In J. S. Gero (Ed.), Design Computing and Cognition (Vol. 10, pp. 77–96). Springer Netherlands.
Clark, H. H. & Brennan, S. E. (1991). Grounding in communication. In L. B. Resnick, J. M. Levine & S. D. Teasley (Eds.), Perspectives on socially shared cognition (p. 127–149). American Psychological Association. https://doi.org/10.1037/10096-006
Committee on the Rights of the Child. (2008). Report of the Committee on the Rights of the Child on its General Discussion on the Right of the Child to Education in Emergencies Situation. Geneva, Switzerland: Office of the United Nations High Commissioner for Human Rights (OHCHR). https://www.right-to-education.org/resource/report-committee-rights-child-its-general-discussion-right-child-education-emergencies
Creese, B. & Isaacs, T. (2016). International instructional systems: How England measures up. The Curriculum Journal, 27(1), 151–165. https://doi.org/10.1080/09585176.2015.1131171
Crilly, N. (2015). Fixation and creativity in concept development: the attitudes and practices of expert designers. Design Studies, 38, 54–91. https://doi.org/10.1016/j.destud.2015.01.002
Derks, D. & Bakker, A. B. (2010). The Impact of E-mail Communication on Organizational Life. Cyberpsychology : Journal of Psychosocial Research on Cyberspace, 4(1). http://www.cyberpsychology.eu/view.php?cisloclanku=2010052401&..
Deserti, A. & Rizzo, F. (2013). Design and the Cultures of Enterprises. Design Issues, 30(1), 36–56. https://doi.org/10.1162/DESI_a_00247
Devictor, X. (2019). 2019 update: How long do refugees stay in exile? To find out, beware of averages. Retrieved 19 February 2020, from World Bank Blogs website: https://blogs.worldbank.org/dev4peace/2019-update-how-long-do-refugees-stay-exile-find-out-beware-averages
Dryden-Peterson, S. (2011). Refugee Education: A Global Review. Geneva: UNHCR Policy Development and Evaluation Service. https://www.unhcr.org/uk/research/evalreports/4fe317589/refugee-education-global-review-sarah-dryden-peterson-november-2011.html
Elliott, G. (2016). Good - better - best? Identifying highest performing jurisdictions. Research Matters: A Cambridge Assessment Publication, 22, 37–38. https://www.cambridgeassessment.org.uk/Images/374682-good-better-best-identifying-highest-performing-jurisdictions.pdf
European Commission. (2019). Forced displacement: refugees, asylum-seekers and internally displaced people (IDPs) [Text]. Brussels: European Civil Protection and Humanitarian Aid Operations. https://ec.europa.eu/echo/what-we-do/humanitarian-aid/refugees-and-internally-displaced-persons_en
Fortus, D., Adams, L. M. S., Krajcik, J. & Reiser, B. (2015). Assessing the role of curriculum coherence in student learning about energy. Journal of Research in Science Teaching, 52(10), 1408–1425. https://doi.org/10.1002/tea.21261
Halstead, J. M. & Affouneh, S. J. (2006). Educating the human spirit in times of conflict: the case of emergency education in Palestine. International Journal of Children’s Spirituality, 11(2), 199–215. https://doi.org/10.1080/13644360600797172
Harper, R., Bird, C., Zimmermann, T. & Murphy, B. (2013). Dwelling in Software: Aspects of the Felt-Life of Engineers in Large Software Projects. In O. W. Bertelsen, L. Ciolfi, M. A. Grasso & G. Papadopoulos (Eds.), ECSCW 2013: Proceedings of the 13th European Conference on Computer Supported Cooperative Work, 21-25 September 2013, Paphos, Cyprus (pp. 163–180). London: Springer.
Hatchuel, A., Le, M. & Weil, B. (2011). Teaching innovative design reasoning: How concept-knowledge theory can help overcome fixation effects. Artificial Intelligence for Engineering Design, Analysis and Manufacturing: AIEDAM, 25(1), 77–92. Scopus. https://doi.org/10.1017/S089006041000048X
Jameson, E., Horsman, R., Macey, D., Gould, T., Rushton, N., Rycroft-Smith, L., … McClure, L. (2020). Ontology: Structure and meaning in the Cambridge Mathematics Framework. Cambridge UK: Cambridge Mathematics. Retrieved from Cambridge Mathematics website: https://www.cambridgemaths.org/Images/ontology-a-summary.pdf
Jirotka, M., Luff, P. & Heath, C. (1993). Requirements for technology in complex environments: tasks and interaction in a city dealing room. ACM SIGOIS Bulletin, 14(2), 17–23. (New York, NY, USA).
Jonassen, D. H. (1997). Instructional Design Models for Well-Structured and Ill-Structured Problem-Solving Learning Outcomes. Educational Technology Research and Development, 45(1), 65–94.
Karseth, B. & Sivesind, K. (2010). Conceptualising Curriculum Knowledge Within and Beyond the National Context. European Journal of Education, 45(1), 103–120. https://doi.org/10.1111/j.1465-3435.2009.01418.x
Kress, G. R. & van Leeuwen, T. (1996). Reading Images: The Grammar of Visual Design. Abingdon, Oxon: Routledge.
Littleton, K. & Mercer, N. (2013). Interthinking: Putting talk to work (1st ed.). Routledge. https://doi.org/10.4324/9780203809433
Maton, K. (2014). Building Powerful Knowledge: The Significance of Semantic Waves. In Palgrave Studies in Excellence and Equity in Global Education. Knowledge and the Future of the Curriculum (pp. 181–197). London: Palgrave Macmillan, London. https://doi.org/10.1057/9781137429261_12
McKenney, S. (2019). Developing the Human, Material, and Structural Aspects of Infrastructure for Collaborative Curriculum Design: Lessons Learned. In J. Pieters, J. Voogt & N. Pareja Roblin (Eds.), Collaborative Curriculum Design for Sustainable Innovation and Teacher Learning (pp. 403–424). Cham: Springer International Publishing. https://doi.org/10.1007/978-3-030-20062-6_22
Moore, R. (2013). Social Realism and the problem of the problem of knowledge in the sociology of education. British Journal of Sociology of Education, 34(3), 333–353. https://doi.org/10.1080/01425692.2012.714251
Oates, T. (2011). Could do better: using international comparisons to refine the National Curriculum in England. The Curriculum Journal, 22(2), 121–150. https://doi.org/10.1080/09585176.2011.578908
Reitman, W. R. (1965). Cognition and thought: an information-processing approach. Wiley.
Ruddock, G. &Sainsbury, M., (2008). Comparison of the English Core Primary Curriculum to those of other high performing countries (No. DCSF-RW048). Slough: NFER.
Schmidt, W. H. (2004). A Vision for Mathematics. Educational Leadership, 61(5), 6.
Schmidt, W. H., Wang, H. C. & McKnight, C. C. (2005). Curriculum Coherence: An Examination of US Mathematics and Science Content Standards from an International Perspective. Journal of Curriculum Studies, 37(5), 525–559.
Schön, D. A. (1983). The Reflective Practitioner How Professionals Think in Action. London: Temple Smith.
Schunn, C. (2008). Engineering Educational Design. Educational Designer, 1(1). https://www.educationaldesigner.org/ed/volume1/issue1/article2/index.htm
Seitamaa-Hakkarainen, P. (2000). Weaving Design Process as a Dual space Search. Helsinki: University of Helsinki. http://www.mlab.uiah.fi/polut/Yhteiskunnalliset/teoria_ill_defined_complex.html
Sen, A. (2020). ‘Powerful’ human rights education’s curriculum problems. Cambridge Journal of Education, 50(4), 409–427. https://doi.org/10.1080/0305764X.2020.1718609
Simon, H. A. (1973). The structure of ill structured problems. Artificial Intelligence, 4(3), 181–201. https://doi.org/10.1016/0004-3702(73)90011-8
Smith, C. L., Wiser, M., Anderson, C. W. & Krajcik, J. (2006). Implications of Research on Children’s Learning for Standards and Assessment: A Proposed Learning Progression for Matter and the Atomic-Molecular Theory. Measurement: Interdisciplinary Research and Perspectives, 4(1–2), 1–98. https://doi.org/10.1080/15366367.2006.9678570
Star, S. L. & Griesemer, J. R. (1989). Institutional Ecology, ‘Translation’ and Boundary Objects: Amateurs and Professionals on Berkeley’s Museum of Vertebrate Zoology, 1907-39. Social Studies of Science, 19(3), 387–420. https://doi.org/10.1177/030631289019003001
UNICEF. (2003). Sharing common goals: UNICEF, faith-based organizations and children. Retrieved 9 September 2020, from UNICEF website: https://www.unicef.org/media/media_4537.html
UNICEF. (2019). Improving access to education for 600,000 out of school children in Sudan. Retrieved 9 September 2020, from https://www.unicef.org/sudan/stories/improving-access-education-600000-out-school-children-sudan
United Nations High Commissioner for Refugees (UNHCR). (2019). Statistical Yearbooks: Figures at a Glance. Geneva: UNHCR. https://www.unhcr.org/figures-at-a-glance.html
Vygotsky, L. S. (1986). Thought and language. Massachusetts: MIT press.
Wheelahan, L. (2007). How competency‐based training locks the working class out of powerful knowledge: a modified Bernsteinian analysis. British Journal of Sociology of Education, 28(5), 637–651. https://doi.org/10.1080/01425690701505540
Youmans, R. J. & Arciszewski, T. (2014). Design Fixation: A Cloak of Many Colors. In J. S. Gero (Ed.), Design Computing and Cognition ’12 (pp. 115–132). Dordrecht, The Netherlands: Springer.
Young, M. (2013). Overcoming the crisis in curriculum theory: a knowledge-based approach. Journal of Curriculum Studies, 45(2), 101–118. https://doi.org/10.1080/00220272.2013.764505
Young, M. (2014, March). The curriculum and the entitlement to knowledge. Presented at the Cambridge Assessment Network Seminar, Magdalen College, University of Cambridge. Retrieved from https://www.cambridgeassessment.org.uk/Images/166279-the-curriculum-and-the-entitlement-to-knowledge-prof-michael-young.pdf
Young, M., Counsell, C., Burn, K. & Chapman, A. (2016). Masterclass in History Education: Transforming Teaching and Learning. London: Bloomsbury Academic.
Young, M., Lambert, D., Roberts, C. & Roberts, M. (2014). Knowledge and the Future School: Curriculum and Social Justice. London: Bloomsbury Academic.
Zuiker, S. J., Piepgrass, N. & Evans, M. D. (2017). Expanding Design Research: From Researcher Ego-Systems to Stakeholder Ecosystems. In M. J. Spector, B. B. Lockee & M. D. Childress (Eds.), Learning, Design, and Technology (pp. 1–28). Cham, Switzerland: Springer. https://doi.org/10.1007/978-3-319-17727-4_74-1