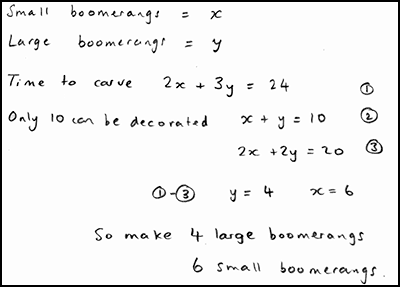The remit for the designers was to create lessons that had clarity of purpose and would maximize opportunities for students to make their reasoning visible to each other and their teacher. This was intended to ensure the alignment of teacher and student learning goals, to enable teachers to adapt and respond to student learning needs in the classroom, and to enable teachers to follow-up lessons appropriately (Black & Wiliam 1998a, 1998b; Leahy, et al. 2005; Swan 2006). The lessons were designed to draw on a range of important mathematical content, be engaging and feature high-level cognitive challenges. They were intended to be accessible, allowing multiple entry points and solution strategies. This allowed students to approach the task in different ways based on their prior knowledge. The lessons were also designed to encourage decision-making, leading to a sense of student ownership. Opportunities for students to conjecture, review and make connections were embedded. Finally, the lessons were designed to provide opportunities for students to compare and critique multiple solution-methods (Figure 1Figure 1).


Developing students’ strategies for problem solving in mathematics:
the role of pre-designed “Sample Student Work”
Sheila Evans and Malcolm Swan
Centre for Research in Mathematics Education
University of Nottingham, England
Summary
iThis paper describes a design strategy that is intended to foster self and peer assessment and develop students’ ability to compare alternative problem solving strategies in mathematics lessons. This involves giving students, after they themselves have tackled a problem, simulated “sample student work” to discuss and critique. We describe the potential uses of this strategy and the issues that have arisen during trials in both US and UK classrooms. We consider how this approach has the potential to develop metacognitive acts in which students reflect on their own decisions and planning actions during mathematical problem solving.
Introduction
iiAn accompanying paper in this volume (Swan & Burkhardt 2014) outlines the rationale, design and structure of the lesson materials developed in the Mathematics Assessment Project (MAP)[1]. In short, the MAP team has designed and developed over one hundred Formative Assessment Lessons (FALs) to support US Middle and High Schools in implementing the new Common Core State Standards for Mathematics. Each lesson consists of student resources and an extensive teacher guide. About one-third of these lessons involves the tackling of non-routine, problem-solving tasks. The aim of these lessons is to use formative assessment to develop students’ capacity to apply mathematics flexibly to unstructured problems, both from pure mathematics and from the real world. These non-routine lessons are freely available on the web: http://map.mathshell.org.uk
One challenge in designing the FALs was to incorporate aspects of self and peer-assessment, activities that have regularly been associated with significant learning gains (Black & Wiliam 1998a). These gains appear to be due to the reflective, self-monitoring or metacognitive habits of mind generated by such activity. As Schoenfeld (1983, 1985, 1987, 1992) demonstrated, expert problem solvers frequently engage in metacognitive acts in which they step back and reflect on the approaches they are using. They ask themselves planning and monitoring questions, such as: ‘Is this going anywhere? Is there a helpful way I might represent this problem differently?’ They bring to mind alternative approaches and make selections based on prior experience. In contrast, novice problem solvers are often observed to become fixated on an approach and pursue it relentlessly, however unprofitably. Self and peer assessment appear to allow students to step back in a similar manner and allow ‘working through tasks’ to be replaced by ‘working on ideas’. Our design challenge was therefore to incorporate opportunities into our lessons for students to develop the facility to engage in metacognitive acts in which they consider and evaluate alternative approaches to non-routine problems.
One of the practices from the Common Core State Standards that we sought to specifically address in this way, was: Construct viable arguments and critique the reasoning of others. Part of this standard reads as follows:
Mathematically proficient students are able to compare the effectiveness of two plausible arguments, distinguish correct logic or reasoning from that which is flawed, and—if there is a flaw in an argument—explain what it is. Students at all grades can listen or read the arguments of others, decide whether they make sense, and ask useful questions to clarify or improve the arguments. (NGA & CCSSO 2010, p. 6)
A possible design strategy was to construct “sample student work” for students to discuss, critique and compare with their own ideas. In this paper we describe the reasons for this approach and the outcomes we have observed when this was used in classroom trials.
The value of critiquing alternative problem solving strategies.
iiiIn a traditional classroom, a task is often used by the teacher to introduce a new technique, then students practice the technique using similar tasks. This is what some refer to as ‘Triple X’ teaching: ‘exposition, examples, exercises.’ There is no need for the teacher to connect or compare alternative approaches as it is predetermined that all students will solve each task using the same method. Any student difficulties are unlikely to surprise the teacher. This is not the case in a classroom where students employ different approaches to solve the same non-routine task; the teacher’s role is more demanding. Students may use unanticipated solution-methods and unforeseen difficulties may arise.
The benefits of learning mathematics by understanding, critiquing, comparing and discussing multiple approaches to a problem are well-known (Pierce, et al. 2011; Silver, et al. 2005). Two approaches are commonly used: inviting students to solve each problem in more than one way, and allowing multiple methods to arise naturally within the classroom then having these discussed by the class. Both methods are difficult for teachers.
Instructional interventions intended to encourage students to produce alternative solutions have proved largely unsuccessful (Silver, et al. 2005). It has been found that not only do students lack motivation to solve a problem in more than one way, but teachers are similarly reluctant to encourage them to do so (Leikin & Levav-Waynberg 2007).
The second, perhaps more natural, approach is for students to share strategies within a whole class discussion. In Japanese classrooms, for example, lessons are often structured with four key components: Hatsumon (the teacher gives the class a problem to initiate discussion); Kikan-shido(the students tackle the problem in groups or individually); Neriage (a whole class discussion in which alternative strategies are compared and contrasted and through which consensus is sought) and finally the Matome, or summary (Fernandez & Yoshida 2004; Shimizu 1999). Among these, the Neriage stage is considered to be the most crucial. This term, in Japanese refers to kneading or polishing in pottery, where different colours of clay are blended together. This serves as a metaphor for the considering and blending of students’ own approaches to solving a mathematics problem. It involves great skill on the part of the teacher, as she must select student work carefully during the Kikan-shido phase and sequence the work in a way that will elicit the most profitable discussions. In the Matome stage of the lesson, the Japanese teachers will tend to make a careful final comment on the mathematical sophistication of the approaches used. The process is described by Shimizu:
Based on the teacher’s observations during Kikan-shido, he or she carefully calls on students to present their solution methods on the chalkboard, selecting the students in a particular order. The order is quite important both for encouraging those students who found naive methods and for showing students’ ideas in relation to the mathematical connections among them. In some cases, even an incorrect method or error may be presented if the teacher thinks this would be beneficial to the class. Once students’ ideas are presented on the chalkboard, they are compared and contrasted orally. The teacher’s role is not to point out the best solution but to guide the discussion toward an integrated idea.
(Shimizu 1999, p110)
In part, perhaps, influenced by the Japanese approaches, other researchers have also adopted similar models for structuring classroom activity. They too emphasize the importance of: anticipating student responses to cognitively demanding tasks; careful monitoring of student work; discerning the mathematical value of alternative approaches in order to scaffold learning; purposefully selecting solution-methods for whole class discussion; orchestrating this discussion to build on the collective sense-making of students by intentionally ordering the work to be shared; helping students make connections between and among different approaches and looking for generalizations; and recognizing and valuing students’ constructed solutions by comparing this with existing valued knowledge, so that they may be transformed into reusable knowledge (Brousseau 1997; Chazan & Ball 1999; Lampert 2001; Stein, et al. 2008). However, this is demanding on teachers. The teachers’ concern that students participate in these discussions by sharing ideas with the whole class often becomes the main goal of the activity. Often researchers observe teachers sticking to a ‘show and tell’ approach rather than discussing the ideas behind the solutions in any depth. Student talk is often prioritized over peer learning (Stein, et al. 2008). Merely accepting answers, without attempting to critique and synthesize individual contributions does guarantee participation, is less demanding on the teacher, but can constrain the development of mathematical thinking (Mercer 1995)
In our work prior to the Mathematics Assessment Project (MAP) project, however, we have found that approaches which rely on teachers selecting and discussing students’ own work are problematic when the mathematical problems are both non-routine and involve substantial chains of reasoning. Teachers have only limited time to spend with each group during the course of a lesson. They find it extremely difficult to monitor and interpret extended student reasoning as this can be poorly articulated or expressed. Most of the ‘problems’ discussed in the research literature are short and contain only a few steps, so the selection of student work is relatively straightforward. We have attempted to tackle this issue by suggesting teachers allow students time to work on the problems individually in advance of the lesson, and then collect in these early ideas and attempt to interpret the approaches before the formative assessment lesson itself. This time gap does allow teachers an opportunity to anticipate student responses in the lesson and prepare formative feedback in the form of written and oral questions. In addition, we have suggested that group work is undertaken using shared resources and is presented on posters so that student reasoning becomes more visible to the teacher as he or she is monitoring work. The selection and presentation of student approaches remains difficult however, partly because the responses are so complex that other students have difficulty understanding them. We often witness ‘show and tell’ events where the students present their approach only to be greeted with a silent incomprehension from their peers.
One possible solution we explore in the rest of this paper, is the use of pre-prepared “sample student work”. This is carefully designed, handwritten material that simulates how students may respond to a problem. The handwritten nature conveys to students that this work may contain errors and may be incomplete. The task for students is to critique each piece and compare the approaches used, with each other and with their own, before returning to improve their own work on the problem.
Here, we explore the use of sample student work in the classroom. We first describe how the sample student work fits into the design of a problem solving FALs; then consider its potential uses, its design and form and then the difficulties that have been observed as it has been used within the classroom. We conclude by discussing the design issues raised and possible directions for future research.
Development of the Problem Solving Lessons: the designers’ remit
ivThe design of the MAP lessons has been explained elsewhere in this volume (Swan & Burkhardt 2014), so we refrain from repeating that here. The process was based on design research principles, involving theory-driven iterative cycles of design, enactment, analysis and redesign (Barab & Squire 2004; Bereiter 2002; Cobb, et al. 2003; DBRC 2003, p. 5; Kelly 2003; van den Akker, et al. 2006). Each lesson was developed, through two iterative design cycles, with each lesson being trialed in three or four US classrooms between each revision. Revisions were based on structured, detailed feedback from experienced observers of the materials in use in classrooms. The intention was to develop robust designs that may be used more widely by teachers, without further support.
 Click to enlarge (4 pages)
Download complete lesson (PDF)
Click to enlarge (4 pages)
Download complete lesson (PDF)
Research indicates that it is not sufficient for teachers to be simply handed non-routine tasks. Lessons such as these can proceed in unexpected ways and, without teacher guidance, can often result in teachers reducing the cognitive demands of the task and the corresponding learning opportunities (Stein, et al. 1996). In order to support teachers in developing skills to successfully work with these lessons, detailed guides were written. The guides outline the structure of each lesson, clearly stating the designers’ intentions, suggestions for formative assessment, examples of issues students may face and offering detailed pedagogical guidance for the teacher.

An example of a problem-solving lesson.
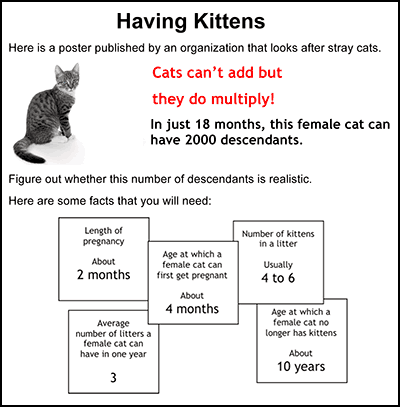
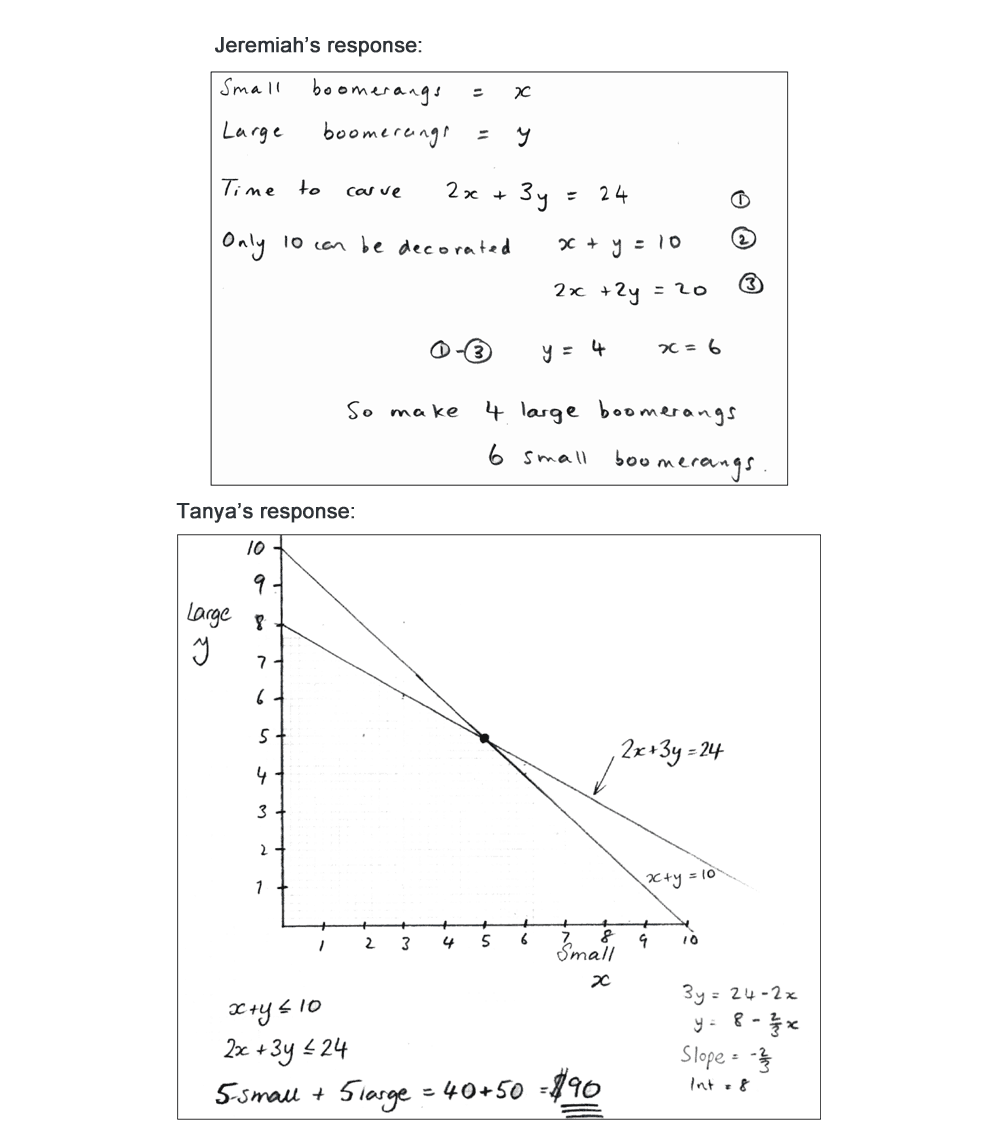
vIn Figure 2 we offer one example of a problem-solving task[2], and below outline a typical lesson structure:
- An unscaffolded problem is tackled individually by students Students are given about 20 minutes to tackle the problem without help, and their initial attempts are collected in by the teacher.
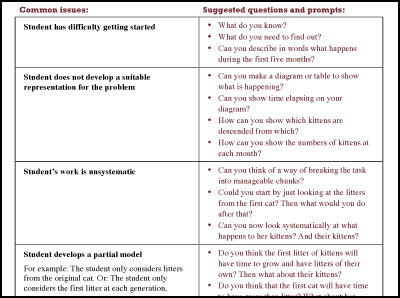
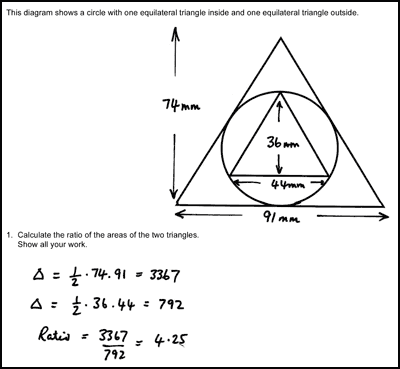
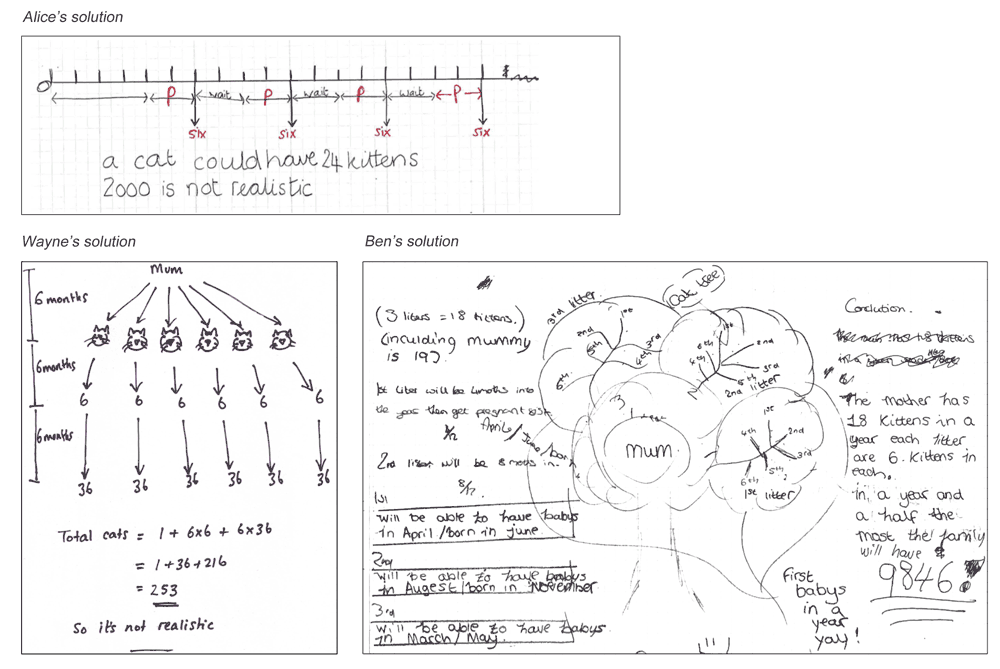
- Teachers assess a sample of the work The teacher reviews the sample and identifies the main issues that need addressing in the lesson. We describe the common issues (Figure 3) that arise and suggest questions for the teacher to use to move students’ thinking forward. (In Having Kittens, these included: not developing a suitable representation, working unsystematically, not making assumptions explicit and so on).
- Groups work on the problem The teacher asks students to work together, sharing their initial ideas and attempt to arrive at a joint, group solution, that they can present on a poster. The pre-prepared strategic questions are posed to students that seem to be struggling.
- Students share different approaches Students visit each other’s posters and groups explain their approach. Alternatively a few group solutions may be displayed and discussed. This may help for example, to begin discussions on the assumptions made, and so on.
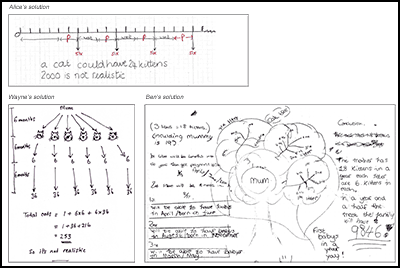
- Students discuss sample student work Students are given a range of sample student work that illustrate a range of possible approaches (Figure 4). They are asked to complete, correct and/or compare these. In the Kittens example, students are asked to comment on the correct aspects of each piece, the assumptions made, and how the work may be improved. The teacher’s guide contains a detailed commentary on each piece. For example, for Wayne’s solution, the guide says: Wayne has assumed that the mother has six kittens after 6 months, and has considered succeeding generations. He has, however, forgotten that each cat may have more than one litter. He has shown the timeline clearly. Wayne doesn’t explain where the 6-month gaps have come from.
- Students improve their own solutions Students are given a further opportunity to act on what they have learned from each other and the sample student work.
- Whole class discussion to review learning points in the lesson The teacher holds a class discussion focusing on some aspects of the learning. For example, he or she may focus on the role of assumptions, the representations used, and the mathematical structure of the problem. This may also involve further references to the sample student work.
- Students complete a personal review questionnaire This simply invites students to reflect on how their understanding of the problem has evolved over the lesson andwhat they have learned from it.
Collect students’ responses to the task. Make some notes on what their work reveals about their current levels of understanding, and their different problem solving approaches. The purpose of doing this is to forewarn you of issues that will arise during the lesson itself, so that you may prepare carefully. We suggest that you do not score students’ work. The research shows that this will be counterproductive, as it will encourage students to compare their scores and will distract their attention from what they can do to improve their mathematics
To, help students to make further progress by summarizing their difficulties as a series of questions. Some suggestions for these are given on the next page. These have been drawn from common difficulties observed in trials of this lesson unit. (extract from the Teacher Guide)
By drawing attention to common issues, the contents of the table can also support teachers to scaffold students learning both during the collaborative activity and whole class discussions.
 Download the complete "Having Kittens" lesson as PDF
(The full
PDF for "Having Kittens" can be viewed online.)
Download the complete "Having Kittens" lesson as PDF
(The full
PDF for "Having Kittens" can be viewed online.)
Sample and data collection
viAltogether, these formative assessment lessons were trialed by over 100 teachers in over 50 US schools. During the third year of the project, many of the problem solving lessons were also taught in the UK by eight secondary school teachers, with first-hand observation by the lesson designers.
Although teachers in all of these trials were invited to teach the lesson as outlined in the guide, we also made it clear that teachers should feel able to adapt the materials to accommodate the needs, interests and previous attainment of students, as well as the teacher’s own preferred ways of working. We recognized that teachers play the central role in transforming the design intentions and, inevitably, that some of these transformations would surprise the designers .
We examined all available observer reports on the problem solving lessons and elicited all references to sample student work. These comments were then categorized under specific themes such as ‘Errors in Sample Student Work’ or ‘Questions for students to answer about sample student work’. Additionally, observers completed a questionnaire (Figure 5Figure 5) designed specifically to help designers better understand how teachers use the sample student work and the supporting guide, and how this use has evolved over the course of the project. This data forms the basis of the findings from the US lesson trials.
The analysis of the UK data is ongoing. Before and after each FAL teachers were interviewed using a questionnaire (Figure 6Figure 6) intended to help designers better comprehend key teacher behaviors and understandings, such as how the teacher prepared for the lesson, what she perceived as the ‘big mathematical ideas’ of the lesson, what she had learnt from the lesson. At the end of the one-year project, teachers were interviewed about their experiences. Again the questions asked were shaped by the literature and issues that had arisen over the course of the project. For example, how teachers used the guide and their opinions on the sample student work. At the time of writing, all the final interviews have been analyzed, as have the pre and post lesson responses made by two of the teachers. We have also developed a framework to analyze whole class discussions. Twelve class discussions have been analyzed. This data forms the basis of the findings from the UK lesson trials.
Potential uses of “Sample Student Work”
viiDuring the refinement of the lessons we have gradually become more aware that the purpose of sharing student approaches needs to be made explicit. By combining purposes inappropriately, we can undermine their effect. For example, if a sample approach is full of errors, the student may become so absorbed in working through the sample work that they fail to make comparisons between different pieces of work.
The following list describes some of the reasons we have designed sample student work:
To encourage a student that is stuck in one line of thinking to consider others
If a student has struggled for some time with a particular approach, teachers are often tempted to suggest a specific approach. This can lead to subsequent imitative behavior by students. Alternatively the teacher may ask the student to consider other students’ attempts to solve the problem. This offers fresh insight and help without being directive.“For students who have had trouble coming up with a solution, having the sample student work has helped them think of a way to organize or get started with the task. Since these students are having trouble getting a solution, they usually look over the various sample student work and pick one with which they feel most comfortable. Having Kittens was one task where students benefitted by seeing how other students organized their thinking”.
(Observer comment from questionnaire)
To enable a student to make connections within mathematics
Different approaches to a problem can facilitate connections between different elements of knowledge, thereby creating or strengthening networks of related ideas and enabling students to achieve ‘a coherent, comprehensive, flexible and more abstract knowledge structure’ (Seufert, et al. 2007).“I did not routinely, except perhaps at A level, make connections between topics and now I am trying to incorporate this into my practice at a much lower level. The sample student work highlighted how traditional my approach was and how I followed quite a linear route of mathematical progression”
(UK teacher during end-of-project interview)Figure 7Figure 7 shows an example of sample solutions provided in the FALs that provide students with opportunities to connect and compare different representations.
- To signal to students that mistakes are part of learning
In so doing the stigma attached to being wrong may be reduced (Staples 2007). - To draw attention to common mathematical misconceptions
A sample piece of student work may be chosen or carefully designed to embody a particular mathematical misconception. Students may then be asked to analyse the line of reasoning embedded in the work, and explain its defects. - To compare alternative representations of a problem
For modelling problems, many different representations are possible during the formulation stage. Typically these include verbal, diagrammatic, graphical, tabular and algebraic representations. Each has its own advantages and disadvantages, and through the comparison of these over a succession of problems, students may become more able to appreciate their power. - To compare hidden assumptions
It is often helpful to offer students two correct responses to a problem that arrive at very different solutions solely because different modelling assumptions have been made. This draws attention to the sensitivity of the solution to the variables within the problem. An example of this is provided by the sample solutions in Figure 3. - To draw students attention to valued criteria for assessment.
Particularly when using tasks that involve problem solving and investigation, students often remain unsure of the educational purpose of the lesson and the criteria the teacher is using to judge the quality of their work (Bell, et al. 1997). If they are asked, for example, to rank-order several pieces of sample student work according to given criteria (such as accuracy, quality of communication, elegance) they become more aware of such criteria. This can contribute significantly to the alignment of student and teacher objectives (Leahy, et al. 2005). Also, engaging in another student’s thinking may strengthen students’ self-assessment skills.
The design and form of sample student work
viiiResearch suggests that students’ self-assessment capabilities may be enhanced if they are provided with existing solutions to work through and reflect upon. Carroll (1994), for example, replaced students working through algebra problems with students studying worked examples. This was shown to be particularly effective with low-achievers because it reduced the cognitive load and allowed students to reflect on the processes involved.
In our work we have frequently found it necessary to design the ‘student work’ ourselves, rather than use examples taken straight from the classroom. This is often to ensure that the focus of students’ discussion will remain on those aspects of the work that we intend. For example, the work must be clear and accessible, if other students are to be able to follow the reasoning. If each piece of work is overlong, then students may find it difficult to apprehend the work as a whole, so that comparisons become difficult to make. If our created student work is too far removed (too easy or too difficult) from what the students themselves would or could do, then it loses credibility.
It was felt important to use handwritten work, as this communicates to students that the work is freshly created and has not been polished for publication. It reduces the perceived ‘authority’ of the mathematics presented, increases the likelihood that it may contain errors and introduces a third ‘person’ to the classroom who is unknown to the students. This anonymity can be advantageous; students do not know the mathematical prowess of the author. If it is known that a student with an established reputation for being ‘mathematically able’ has authored a solution then most will assume the solution is valid. Anonymity removes this danger. Making ‘student work’ anonymous also reduces the emotional aspects of peer review. Feedback from our early trials indicated that sometimes students were reserved and over-polite about one another’s work, reluctant to voice comments that could be perceived as negative. When outside work was introduced, they became more critical.
Students needed exposure to a wide range of methods
ixIn the US trials, we found that, within a single class, the solution methods used by students were often similar in kind. This may be partly due to the common practice of US teachers to focus exclusively on each topic area for an extended period, thus making it likely that students will draw from that area when solving a problem. Alternatively, students may choose to use a solution method they assume is particularly valued, even when this might be inappropriate. The following observer comment would suggest that a numerical solution would be favored over a geometric one, for example:
Due to the ‘traditional’ approaches generally used here in the States, many teachers believe that ‘geometric’ solutions are NOT showing rigor or intelligence and that number is the best way. Students have internalized this… (Observer report)
In our experience, students are unlikely to draw autonomously on methods they are still unsure of or they have only just learned. The mathematics they choose to use will often relate back to mathematics used in earlier years. They may frequently resort, for example, to safe and inefficient ‘guess and check’ numerical methods, that they know they can rely on, rather than graphical or algebraic methods.
The difficulty of transferring methods from one context to another is a common theme in the research literature. For example, students may know how to figure out the gradient, intercept and the equation of a graph, but still find it challenging to recall and apply these concepts to a ‘real-world’ problem. One reason for the low degree of transfer is that students often recall concepts in a situation-specific manner, focusing mainly on surface features (Gentner 1989; Medin & Ross 1989) rather than on the underlying mathematical principles. Our UK study supports these findings. On several occasions teachers taught a concept, in advance of the lesson, that they considered would help students to solve the problem and were subsequently surprised that students decided not to use it! Clearly, successful problem solving is not just about students’ knowledge - it is about how, when and whether they decide to use it (Schoenfeld, 1992, p. 44).
In the few cases where students did use a wide range of approaches, these rarely included strategies to match all the learning goals of the lesson. For example, students did not necessarily select different representations of the same concept, or use efficient, elegant or generalizable strategies. The mathematical learning opportunities were therefore limited.
For the above reasons we concluded that some fresh input of methods needed to be introduced into the classroom if students were to have opportunities to discuss alternative representations and powerful methods. This could perhaps come from the teacher, but that would then almost certainly remove the problem from students and result in students imitating the teacher’s method. Sample student work provides an alternative input that, as we have said, carries less authority.
Difficulties in using sample student work in the classroom.
xIn this section we outline a few of the main difficulties we observed when sample student work was used in US and UK classrooms.
Students were analyzing work in superficial ways
1In our first version of the teacher’s guide, we suggested that the teacher could introduce the sample work to the class by writing the following instructions on the board:
Imagine you are the teacher and have to assess this work. Correct the work and write comments on the accuracy and organization of each response. Make some specific suggestions as to how the work may be improved.
Feedback from the US trials indicated that these instructions were inadequate. Teachers and students were not clear on the purposes of the activity, and student responses were superficial. For example, observers reported US teachers asking:
What is the math we want to have a conversation about? Do we want students to explain the method? Do we want each piece to stand-alone or should students compare and contrast strategies?
Observers reported that students were not digging deeply enough into the mathematics of each sample and, unless asked a direct question by the teacher, they often worked in silence, looking for errors without evaluating the overall solution strategy. Some students mimicked the feedback they often received from their teacher, providing comments such as ‘Awesome’, ‘Good answer’ or ‘Show a little more work’. A clear message came from the observers; the prompts in the guide needed to be more explicit and focus on the mathematics of the problem; scaffolding was required. The decision was therefore made to include more specific questions, such as:
What piece of information has Danny forgotten to use? What is the purpose of Lydia’s graph? What is the point of figuring out the slope and intercept?
Such questions appeared to make the purpose more discernable to teachers. Feedback from the US observers to these changes was encouraging:
I think the questions or prompts about each piece of student work really focus the students on the thinking, bring out the key mathematics and are a great improvement to the original lesson…Last year students just made judgment statements, but this year the comments were focused on the mathematics.
Not all teachers shared this view, however. In the UK, one teacher commented:
Students are being forced along a certain path as a way to engage with the sample student work. Rather, they [the questions] should be more open and students are then able to comment in any way they like. …. I think sometimes they feel themselves kind of shoehorning in certain types of answer.
This teacher preferred to simply ask students to explain the approach; describe what the student had done well and suggest possible improvements. This practice did encourage engagement, and students’ assessment criteria were made visible to the teacher, but at times the learning goals of the lesson were only superficially attended to.
In both the US and UK, many students focused on the appearance of the work, rather than on its content, with comments on the neatness of diagrams and handwriting. Many commented that the sample work was poorly explained, but did not go on to say clearly how it should be improved. Sample comments were: ‘she needs to explain it better’; ‘the diagrams should not be all over the place’. We attempted to remedy this by suggesting that, rather than just making suggestions for improvement, students should actually make improvements. One teacher commented that this focus on effective mathematical communication had resulted in her students writing fuller explanations when solving problems for themselves.
Students were focused on correcting errors, while ignoring holistic issues
2The feedback from observers on the use of errors in sample student work presented us with a more complex issue. Observers commented that when understandings were fragile, the errors often made ‘the most complicated ideas more complicated’. It also became apparent from US feedback that when errors were found in sample student work, some students dismissed the solutions as undeserving of further analysis. Similarly, in UK classrooms students and teachers often assumed the only goal of the activity was to locate and correct errors. One UK teacher commented that when the student work was error-free, students were more inclined to make holistic comparisons of strategic approach.
This led us to look carefully at our purposes in using errors. We had originally included two different kinds of errors: procedural and conceptual. Procedural errors are common arithmetic or algebraic mistakes. Conceptual errors are symptoms of incorrect reasoning and are often more structural in nature. In response to feedback from observers, we removed many of the procedural errors. In many cases, however, the design decision was taken to retain conceptual errors that encourage students to understand the solution-method and its purpose.
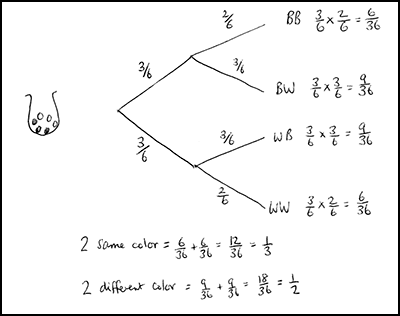
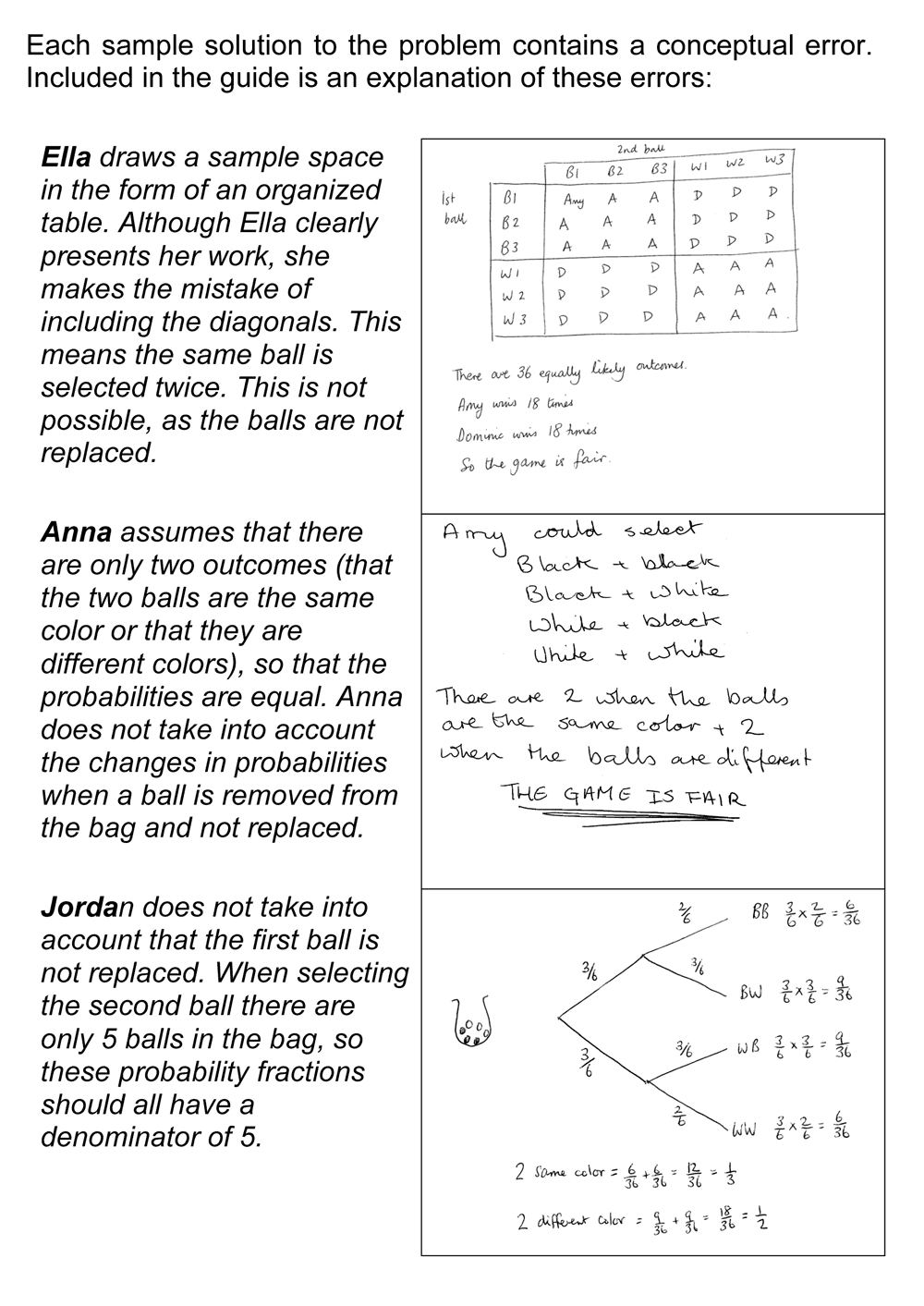
For example, Figure 10 shows a problem solving task and Figure 11 shows three samples of student work. Each sample contains a conceptual error. Included in the guide is an explanation of these errors:
Ella draws a sample space in the form of an organized table. Although Ella clearly presents her work, she makes the mistake of including the diagonals. This means the same ball is selected twice. This is not possible, as the balls are not replaced.
(Teacher’s guide)Anna assumes that there are only two outcomes (that the two balls are the same color or that they are different colors), so that the probabilities are equal. Anna does not take into account the changes in probabilities when a ball is removed from the bag and not replaced.
Jordan does not take into account that the first ball is not replaced. When selecting the second ball there are only 5 balls in the bag, so these probability fractions should all have a denominator of 5.
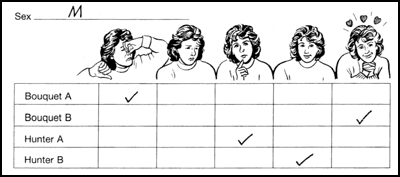
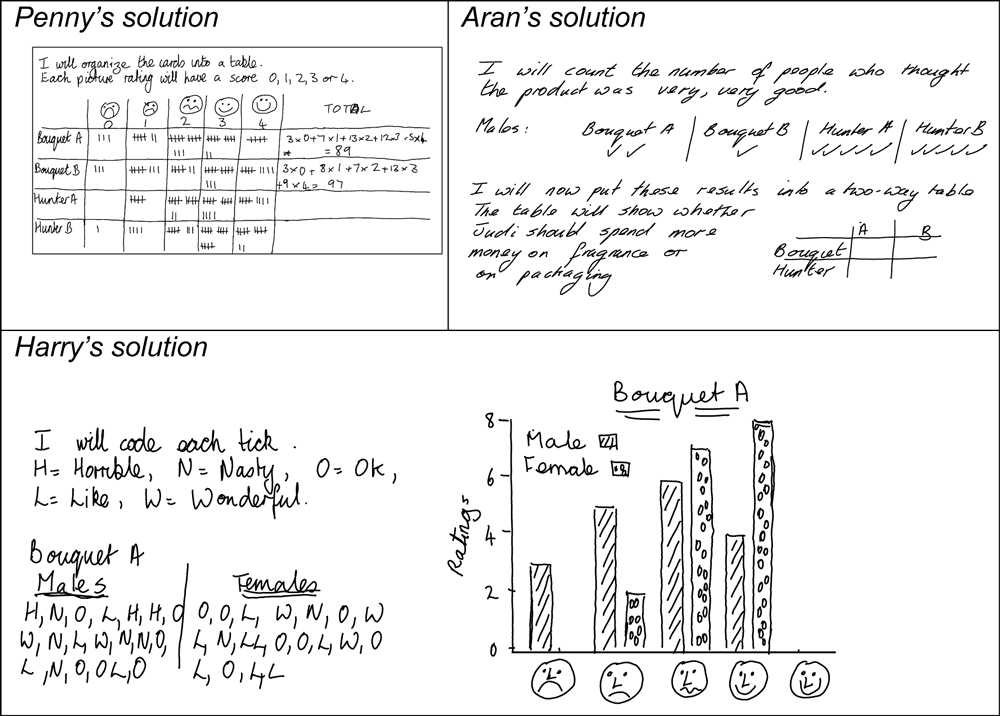
In some lessons we decide that, rather than including errors, we invited students to complete unfinished responses. For example, in the Testing a New Product task (Figure 12) students’ were asked to complete the tables in Penny and Aran’s work and the final column in Harry’s graph (Figure 13).
They were then asked to describe the advantages and disadvantages of each approach to the problem. Most students in a UK trial of the lesson were able to complete the work, they understood the processes, and were able to work out the correct answers. They did however encounter difficulties interpreting the resulting figures in the context of the real-world situation. This struggle prompted students to consider how far each approach is fit for purpose: how well it each one tackles the problem of working with the four variables of packaging, fragrance, gender and preference, and how far useful conclusions may be reached using each approach.
Students were not given time to consider a sufficient range of sample student work
3Initial feedback from observers indicated the lessons were taking longer than had been anticipated; teachers were giving out all pieces of sample student work, but there was often insufficient time for students to successfully evaluate and compare the different approaches. In response to this, designers included the following generic text to all lessons guides:
There may not be time, and it is not essential, for all groups to look at all sample responses. If this is the case, be selective about what you hand out. For example, groups that have successfully completed the task using one method will benefit from looking at different approaches. Other groups that have struggled with a particular approach may benefit from seeing another student’s work that uses the same strategy.
These instructions encourage students to critique and reflect on unfamiliar approaches, to explicate a process and to compare their own work with a similar approach; this, in turn could serve as a catalyst to review and revise their own work. Differentiating the allocation of sample student work in this way may however create problems in the whole class discussion, as not all of the students will have worked on the piece of work under discussion. This instruction places pedagogical demands on teachers, however. They have to again make rapid decisions on which piece of work to allocate to each group. In US trials, however, the suggested approach was not followed:
We have some teachers who give all the sample student work and let students choose the order and the amount they do. This might be less common. Others are very controlling and hand out certain pieces to each group. Others like a certain method to solve problems and like to use that one to model. I think this is a function of the teacher’s comfort level with control and students expectations. (Observer report)
It turned out that very few students were allowed sufficient time to work on all the pieces of sample student work or time to evaluate unfamiliar methods.
These issues were also a concern for the UK teachers. At the start of the project some were reluctant to issue all of the sample student work at the same time, for fear that students would be overwhelmed. As one teacher commented:
At the beginning (of the project) it was too much for pupils to take on all the different methods at once. Even towards the end I didn’t always give them all to them. I believed they became unsettled because the task felt too great. I felt they needed to get used to just looking at one piece first. I also picked out pieces of work that I felt within their ability they could access. (Teacher report)
Students were not using the sample student work to improve their own solutions
4Although the teachers clearly recognized that a prime purpose of sample student work was to serve as a catalyst for students to ultimately improve their own solutions, there was little evidence of students subsequently changing their work apart from when they noticed numerical errors. While most students acknowledged that their work needed improving, many did not take the next step and improve it. Only students that were stuck were likely to adapt or use a strategy from the sample student work.
The problem solving lessons were designed to involve cycles of refinement of students’ solutions. They attempted the task individually, before the lesson, then in groups, then considered the sample work and then again were urged to improve their work a third time. For teachers that were used to students working through a problem once, then moving on, this was a substantial new demand.
It is clear that communicating complex pedagogic intentions is not easy. It is made easier by having some common framework with reference points. A strategic goal of these lessons was to build this infrastructure in teachers’ minds
Students were often not invited to make comparisons between the sample approaches.
5As mentioned earlier in the paper, the design intention is for students to compare alternative problem solving approaches. As such, all lessons include whole-class discussion instructions of the following kind:
Ask students to compare the different methods: Which method did you like best? Why? Which method did you find most difficult to understand? Why? How could the student improve his/her answer? Did anyone come up with a method different from these?
Feedback from both the US and UK classrooms indicate that teachers rarely encouraged students to make such comparisons. There appear to be multiple reasons for this.
Time pressure was a frequently raised issue. Students need sufficient time to identify and reflect on the similarities and differences between methods and connect these to the constraints and affordances of each method in terms of the context of the problem. The whole class discussion was held towards the end of the lesson. These discussions were often brief or non-existent, possibly reflecting how teachers value the activity. A common assumption was that the important learning had already happened, in the collaborative activity.
Another factor may be lack of adequate support in the guide. Research indicates it is not enough to simply suggest that sample student work should be compared, there need to be instructional prompts that draw students’ attention to the similarities and differences of methods (Chazan & Ball 1999). Teachers and students need criteria for comparison to frame the discussion (Gentner, et al. 2003; Rittle-Johnson & Star 2009). Furthermore, these prompts should occur prior to the whole-class discussion. Students need time to develop their own ideas before sharing them with the class.
Rather than compare the different pieces of sample student work, UK students were consistently given the opportunity to compare one piece with their own. Students often used the sample to figure out errors either in their own or in the sample itself. One UK teacher noted that when groups were given the sample student work that most closely reflected their own solution-method, their comments appeared to be more thoughtful, whereas with unfamiliar solution-methods students often focused on the correctness of the result or the neatness of the drawing and did not perceive it as a solution-method they would use.
Discussion of the design issues raised
xiMost of the teachers involved in the trials had never before attempted to ask students to critique work in the ways described above. They reported that ‘getting inside another person’s head’ proved challenging and students learned to do this only gradually.
I think it has taken most of the year to get the kids to actually be able to look at a piece of work and follow it through to see what that person has done …..
One of the profound difficulties for designers is in trying to increase the possibilities for reflective activity in classrooms. The etymology of the word curriculum is from the Latin word for a race or a racecourse, which in turn is derived from the verb currere meaning to run. Perhaps unfortunately, that is precisely what it feels like for most students. The introduction of problem solving in general, and of analyzing sample student work in particular are seen by many as time-consuming activities that detract from the primary goal of improving procedural fluency or ‘learning more stuff’.
We are encouraged, however to see that the new Common Core State Standards place explicit value on the development of problem solving, mathematical practices and, in particular, on students being able to critique reasoning. Most students, we suspect, are not aware of this new agenda. Some years ago, we conducted an experiment to see whether students could identify the purposes of a number of different kinds of mathematics lesson. It became clear that students’ and teachers’ perceptions of the purposes of the lessons were only aligned for procedural mathematics. The mismatch between teacher and student perceptions was more pronounced as lessons became progressively more practices-oriented (Swan, et al. 2000). There was some empirical evidence, however, that by introducing metacognitive activities into the classroom that this mismatch could be reduced. These included such activities as discussing key conceptual obstacles and common errors, explaining errors in sample student work – and orally reviewing the purpose of each lesson.
In this paper, we have seen that, left to themselves, students are unlikely to produce a wide range of qualitatively different solutions for comparison, and therefore it may be helpful to create samples of work to stimulate such reflective discussion. We have, however also noted that we have found it necessary to:
- discourage superficial analysis, by stating explicitly the purpose of the sample student work, and by asking specific questions that relate to this purpose;
- encourage holistic comparisons by making the sample student work short, accessible and clear, and by not including arithmetic and other low-level errors that distract the students’ attention away from the identified purpose;
- make the distribution of the sample student work more effective, by perhaps sequencing it so that successive pairwise comparisons of approaches can be made;
- offer students explicit opportunities to incorporate what they have learned from the sample work into their own solutions;
- offer the teachers support for the whole class discussion so that they can identify and draw out criteria for the comparison of alternative approaches.
From a designers’ perspective, it is natural to focus on the challenges in creating a design that may be used effectively by the target audiences. We may thus have given the impression that the lessons have been unsuccessful in achieving their goals. This, however, is far from the truth. These lessons are proving extremely popular with teachers and are currently being used as professional development tools across the US. They are also forming the basis for ‘lesson studies’ in both the US and the UK. In the lesson studies, they are viewed as ‘research proposals’ rather than ‘lesson plans’.
Teachers and observers have described on many occasions the learning they have gained from comparing student work in these lessons; teacher comments include:
I now think pupils can learn more from working with many different solutions to one problem rather than solving many different problems, each in only one way.
It moves away from students chasing the answer.
I can now see how much easier it is for a student to recognize that, say a trial and improvement method is inefficient, when it is compared to a sleek geometrical method rather than when simply looking at the solution on its’ own.
To our knowledge, there are no major studies that focus on how teachers work with a range of pre-written solution-methods for a range of non-routine problems. This study raises many issues and in so doing acts as a launch pad for further more detailed studies. More exploration is required into how the use of sample student work affects pupils’ capacity to solve problems. One might expect to see, for example, that students increase their repertoire of available methods when solving problems. So far, however, we have no evidence of this. We do, however, have some early indications that students are beginning to write clearer and fuller explanations as a result of critiquing sample student work.
Acknowledgements
xiiWe would like to acknowledge the support for the study, the Bill and Melinda Gates Foundation, our co-researchers at the University of Berkeley, California and the observer team.
[1] The Maths Assessment Project, based at UC Berkeley, was directed by Alan Schoenfeld, Hugh Burkhardt, Daniel Pead, Phil Daro and Malcolm Swan, who led the lesson design team which included at various stages Nichola Clarke, Rita Crust, Clare Dawson, Sheila Evans, Colin Foster and Marie Joubert. The work was supported by the Bill & Melinda Gates Foundation; their program officer was Jamie McKee. The US observers who provided the feedback from US classrooms were led by David Foster, Mary Bouck and Diane Schaefer, working with Sally Keyes, Linda Fisher, Joe Liberato and Judy Keeley.
[2] The Having Kittens task used in this lesson was originally designed by Acumina Ltd. (http://www.acumina.co.uk/) for Bowland Maths (http://www.bowlandmaths.org.uk) and appears courtesy of the Bowland Charitable Trust.
References
xiiiNGA, & CCSSO (2010). Common Core State Standards for Mathematics. Retrieved from http://www.corestandards.org/Math
Swan, M., & Burkhardt, H. (2014). Lesson Design for Formative Assessment. Educational Designer, 2(7). This issue. Retrieved from: http://www.educationaldesigner.org/ed/volume2/issue7/article24
About the Authors
xivSheila Evans is a member of the Mathematics Assessment Project team in the Centre for Research in Mathematical Education at the University of Nottingham. For the last four years she has worked designing, observing, teaching, revising and providing professional development for the MAP Formative Assessment Lessons. She is currently working on a doctorate using teaching resources that have been shaped by this project. Before that, she taught for fifteen years in secondary schools in the UK and Africa, and wrote a textbook Access to Maths aimed at students without traditional qualifications who wished to study at University .
Malcolm Swan is Director of the Centre for Research in Mathematical Education at the University of Nottingham, which incorporates the Shell Centre for Mathematical Education team. He has led the design teams in a sequence of research and development projects. He led the diagnostic teaching research program that established many of the design principles set out in this paper. In 2008 he was awarded the first ISDDE Prize for educational design, for The Language of Functions and Graphs.