Mapping HOTmaths Lessons to the Common Core State Standards for Mathematics
Abstract
This article reports on a collaborative project between Cambridge Mathematics and HOTmaths, where the Cambridge Mathematics Framework was used to map HOTmaths fraction lessons to the fractions content in the USA’s Common Core State Standards for Mathematics, with focus on grades 3-8. This article describes the project, the processes involved in training the HOTmaths team to use the Cambridge Mathematics Framework to map their content onto the Common Core State Standards, and outcomes of the collaboration, such as using the mappings to identify places where HOTmaths lessons did not flow well. The article also gives some recommendations for future research.
Background and introduction
Cambridge Mathematics and HOTmaths
Cambridge Mathematics (CM) is a team of ex-maths teachers, designers, researchers and programmers who are re-thinking support for curriculum design in mathematics teaching and learning (https://www.cambridgemaths.org/). The team is developing the Cambridge Mathematics Framework (CMF, also referred to below as the Framework) – a digital, interactive, and flexible map of mathematics learning for 3-19-year-olds (Majewska, 2021). The team reads and synthesises research in the fields of mathematics, mathematics education, educational psychology, learning sciences and similar areas, which informs the CMF, providing the evidence-based foundations for this tool (Jameson, 2019).
HOTmaths (HM) is a “comprehensive mathematics learning system” developed by designers, educators, and technicians. The HM group, which is based in Australia, has created interactive online mathematics teaching, learning and assessment resources for students, teachers, individuals, and classes (https://www.hotmaths.com.au/).
The term curriculum is used in this article to denote the descriptors provided by an educational body or national organisation that indicate the intended learning of a course or period of study. Examples include the English national curriculum, the Common Core State Standards, and the Australian curriculum.
The project
The HM team were asked by an external client to design lessons for a course based on existing HOTmaths material, whilst ensuring that the lessons were aligned to the Common Core State Standards for Mathematics (CCSSM). The Common Core State Standards are “a set of academic standards in mathematics and English language/arts literacy”, which were developed with the support of the Council of Chief State School Officers and the National Governors Association (NCTM, n.d., para 1). The standards are learning goals that set out the knowledge and skills students should attain by the end of each school year [grade] (Common Core State Standards Initiative, n.d.). The existing HM material was written based on the experience and expertise of the writers from the team to meet the local Australian curriculum specifications. To meet the demands of the task, the HM team decided to collaborate with the CM team.
Aims of the project
The CMF was used as a tool to interrogate HM material for any gaps in content and was used to identify how any missed areas of learning could be covered to enable smooth learning progression. The CMF was mapped onto the HM material with the intention of covering fractions for grades 3 to 8. The HM material for each grade is divided into topics and lessons. The project intended to quality-assure the HM content for the clients.
The CM and HM teams made maps of the HM lesson content and the CCSSM using the CMF as a reference tool to compare and contrast the content and progressions in the HM lessons and the CCSSM. It helped to identify inconsistencies, where the designed resources didn't meet the requirements of the CCSSM. It supported adaptation of the HM resources to promote coherent and connected progressions and analysed the depth, breadth, and flow of HM’s library of content.
This adaptation for the CCSSM was extensive, and included language changes, rearrangement of materials to suit a different age group, new material and changes to teaching and learning techniques. Mapping the HM content to the CMF aimed to identify whether the flow of ideas has been interrupted during this process, and if further learning material was needed to provide a complete coverage of the CCSSM content, including all key learning concepts.
The HM team saw the CMF as a comprehensive tool for not only identifying mathematical concepts, but also in linking these concepts to each other. These links are important when developing learning materials that do not simply contain isolated learning tasks, but rather aim to create connected activities that allow students to relate mathematical concepts to one another. To achieve this ambitious goal, the fractions content of the CCSSM was examined.
This article will demonstrate the impact of using the Framework to map the CCSSM to HM lesson content on fractions from grade 3 to 8. It will also discuss the usefulness of this approach to conduct a deep-gap analysis of mathematical content, which could be beneficial to many designers and researchers.
Enlarge…
The Cambridge Mathematics Framework
The CMF is a design tool which identifies, describes and connects mathematical ideas that are seen as important for learning mathematics. These ideas are represented as waypoints within saved searches and are supported by in-depth literature reviews. The Framework emphasises flexibility with no strict, absolute order for mathematical learning and experiences for learners. It is curriculum-agnostic, aiming to support designers, teachers, and other professionals to explore the possible outcomes of different paths and different choices made about teaching/designing mathematics (Jameson, 2019).
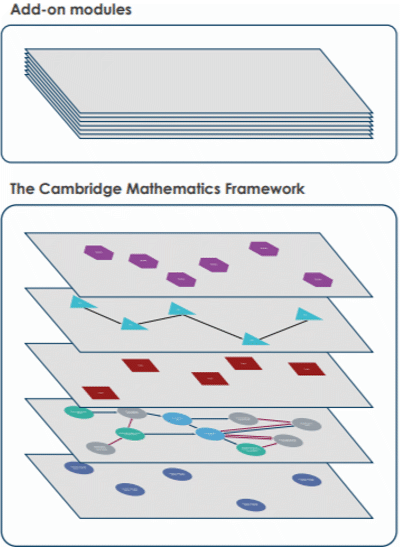
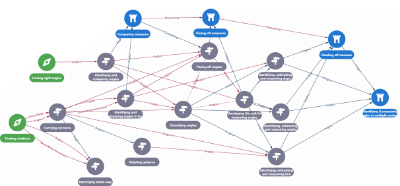
As the CMF is complex, there are linked layers which represent its components as shown in Figure 1 (Jameson, Horsman, Macey et al., 2020). The research layer (which underpins other layers) contains summaries of research in various topics in mathematics education. It also contains research nodes (points which map onto specific research sources and contain meta-data describing these sources) connected by research edges (Jameson, Horsman, Macey et al., 2020, p.14).
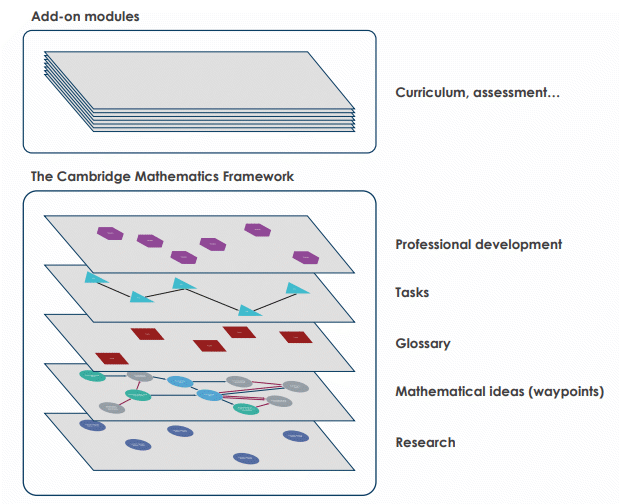
The mathematical ideas layer above the research layer contains mathematical concepts (waypoints) and the relationships between them. It is built in a graph database (Neo4j) from which a platform called CMF Nexus was developed by the team’s programmer - Ben Stevens (Jameson, Horsman, Macey et al., 2020). In the figures in this paper, waypoints are green, light blue or grey. Waypoints refer to “places where learners acquire knowledge, familiarity or expertise about some form of mathematical idea” (Cambridge Mathematics, n.d.). Edges between waypoints indicate a connection and can be directed and undirected. Directed edges, signified by a small arrow, suggest some kind of logical left-to-right implication between the waypoints. Undirected edges do not imply a specific direction or sequence of development (Jameson, Horsman, Macey et al., 2020). To illustrate this, let’s look at the example of waypoints involving ‘making 2D tessellations and tilings’ and ‘analysing properties of 2D shapes’. Although they are clearly related (and hence there is an edge between them), students’ knowledge about the two waypoints can be developed synchronously. Hence the edges connecting them are undirected. In contrast, waypoints exploring linear movement were identified as logically prerequisite to the idea of translational symmetry, so the edges connecting them are directed. For more information about the types of edges, see Jameson, Horsman, Macey et al., 2020).
Enlarge…
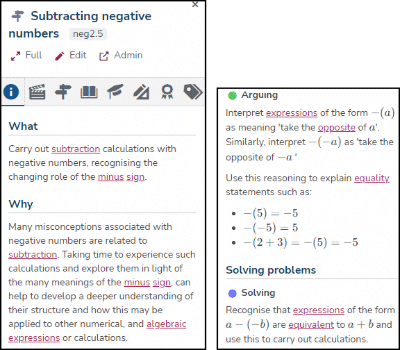
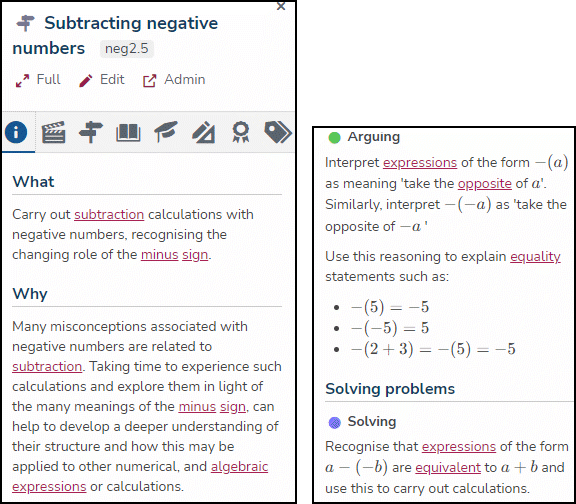
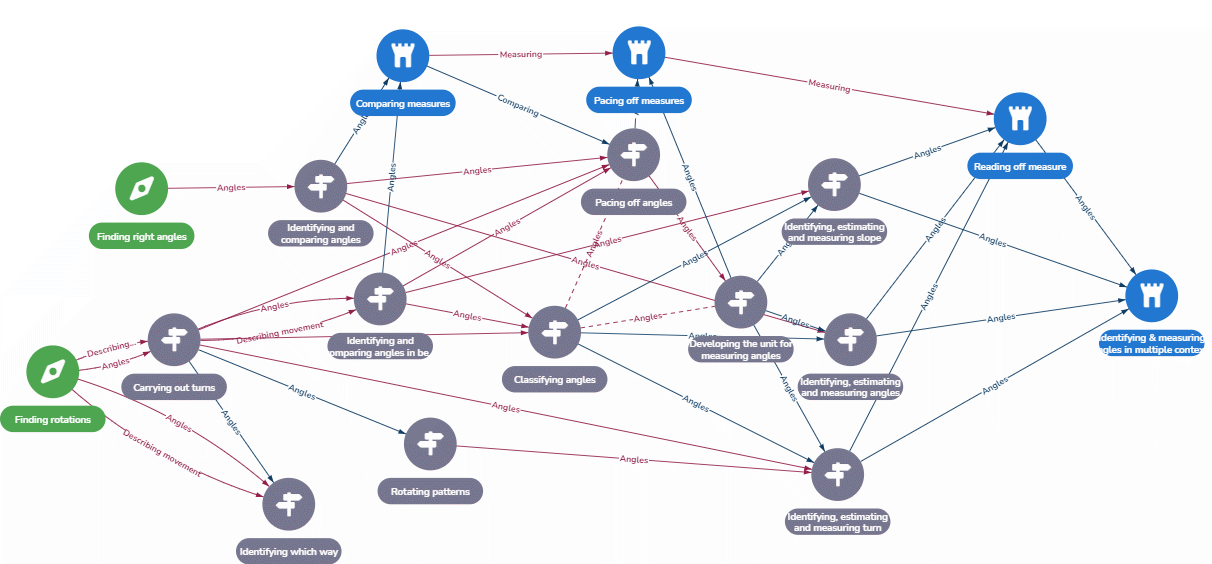
All waypoints have the same structure and contain a ‘what’ and a ‘why’ section and a list of ‘student actions’. Figure 2 shows an example. The ‘what’ section summarises the mathematical idea, whereas the ‘why’ section contains an explanation of the underlying mathematical concepts and what mathematical foundations the waypoint is supporting. The ‘why’ section justifies the inclusion of the waypoint in the Framework map. ‘Student actions’ are examples of potential student behaviours or activities concerning the mathematical idea. The ‘student actions’ were developed from the task design framework of Malcolm Swan where balance was encouraged between performance, conceptual understanding and problem solving in mathematics for all learners at every stage of their education (Swan, 2014, 2015). All waypoints also have a unique identification code attached to them (for instance fra3.1), which corresponds to the topic they are linked to (e.g., ‘fra’ refers to ‘fractions’). There are three types of waypoints: standard waypoints (grey), exploratory waypoints (green) and landmark waypoints (light blue). For more information about waypoints, see Jameson, Horsman, Macey et al., 2020.
Enlarge…
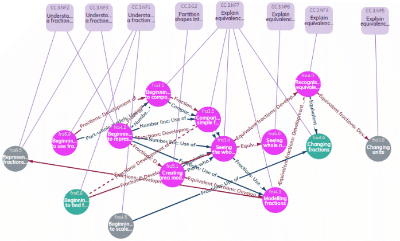
Collections of waypoints and edges in the mathematical layer are known as ‘saved searches’ – interactive portions of the Framework map. Waypoints in the mathematical layer are linked to research nodes (dark blue). An example is shown in Figure 3. Colour coding of the edges is also used to describe the nature of links.
The map of mathematical ideas does not propose timings or age suggestions (Jameson, Horsman, Macey et al., 2020) but leaves the user to make decisions. The Framework is not ‘the’ definitive map of mathematical concepts. Instead, it is one potential structure that enables users to reflect on their own conceptualisations and the coherence of content and progressions in lessons, schemes of work, or curriculum. The add-on modules, shown at the top of Figure 1, contain other kinds of content that link back to the waypoints in the mathematical layer. Mapping HM lesson content to the CCSSM can be thought of as existing in this add-on modules layer.
Why Cambridge Mathematics were selected for this project
The CM team has previously conducted case studies similar to this one, which have been used by various organisations to inform their work, products and resources. For instance, Jameson (2020) describes how a Canadian EdTech company called Vretta used the CMF to gain insights into their educational tasks by aligning some of their MathemaTIC tasks to the CMF. Furthermore, Jameson and Horsman (2020) and Johnson et al. (2021), report how the CMF was used in a large-scale UNICEF-Cambridge project, which aimed to “develop a mathematics curriculum for education in emergency (EIE) situations” (p. 3) to support students who have been displaced and do not have access to formal schooling. These examples illustrate how the CMF can be very useful to educational designers and curriculum developers in contexts like this one.
Training
In September 2020, the HM and CM teams met online to discuss the structure, aims and outcomes of this collaborative project. The teams agreed on an agenda of weekly sessions focusing on the ‘fractions’ component.
A training schedule was created to familiarise the HM team with the design, content, and functionality of the Framework, and consisted of online meetings supported by detailed instructions of how to use the Framework. This was to enable the HM team to create interactive maps of the sections of the Framework pertaining to the fractions material in the HM course. Each session covered additional aspects of the Framework interface, building on what was covered in earlier sessions. Training sessions included discussions about the design of the Framework (including the philosophy and design principles behind it), and workshops demonstrating and trialling how to navigate (search and explore content), how to identify connected pathways or networks between waypoints and how to connect in curriculum statements. These discussions and workshops were accompanied by suggested reading taken from the research section and blog section of the CM website.
The HM team started by identifying the CCSSM standards covering fractions (in grades 3 to 8) and the relevant HM lessons. The boundary of what was meant by the ‘fractions’ component was recognised as ‘fuzzy’ and shared discussions helped clarify what content would and would not be included in this project.
The CM and HM teams met on Zoom twice each week for 5 weeks. As the HM team are based in Australia, the meetings were scheduled for very late evening in England, which corresponded with the start of the working day in Australia. During these meetings, a member of the CM writing team followed the training schedule to develop the HM team’s confidence and skills in using the CMF. The second meeting typically occurred 12 hours after the first meeting. This gave the HM team a whole day to explore the Framework, allowing them to identify questions for the second meeting or to discuss any issues they encountered. Meetings were recorded and notes were taken to inform the project and to learn lessons about what benefits external organisations working with the CMF tool.
Every week, the CM team member involved in this project gave the HM team a task. The tasks increased in complexity. For instance, within a few weeks, the HM team was tasked with mapping individual waypoints to HM lessons and towards the end of the project, they mapped all of their lessons on fractions to the CMF. Overall, HM created mappings for all the CCSSM-relevant lesson content.
Training took a couple of weeks, after which HM created their own saved searches for collections of lessons. They had regular meetings with CM team members to check on their progress and issues. Once HM had mapped their lessons, the CM team compared the HM mappings to their own CCSSM mappings, producing new saved searches. The HM team then explored these mappings, and any issues or questions were dealt with in meetings or via e-mails.
Within a few weeks of training, the HM team designed all lessons using lists of content and learning goals as well as mapping the mathematical ideas to see the flow and continuity throughout a complete topic. The summaries confirmed that the content of the existing HM lessons aligned substantially with educational research pertaining to the study of fractions.
Varieties of useful mappings
Mapping the CCSSM
The CM team mapped the mathematical content explicitly stated in the CCSSM without considering the HM lessons. They designed and created two styles of mappings: minimal and neighbourhood. Minimal maps contained waypoints that were the ‘best match’ for the mathematics explicitly described in the CCSSM. Often, one CCSSM standard was connected to multiple waypoints, and individual waypoints were at times connected to multiple standards. Also, the created maps frequently contained collections of waypoints that were not connected to each other in the CMF, and therefore were considered disjointed and hence needed connecting ideas to be identified.
The functionality of the Framework was then used to identify pathways between the waypoints in the minimal mapping. Again, there were nuances in the way that this was achieved. Firstly, the existence of pathways was verified using the ‘shortest paths’ function of the Framework. This helped identify content that seemed unconnected including where foundational ideas seemed to be missing. The connecting waypoints on these pathways were then added, as were all other pathways. These new mappings also incorporated highly connected waypoints: those with multiple themes passing through whilst connecting the waypoints in the minimal maps. These new ‘neighbourhood maps’ were refined, resulting in a connected coherent map that contained the chosen standards.
The flexibility of the Framework enabled these mappings to be constructed and analysed in different ways. Each grade could be explored looking at the coherence between the topic areas and additionally the topic areas could be explored through the grades to see the developmental pathway of a topic.
Analysing the mappings
Once both teams had completed their mappings, they were analysed together for each topic area and grade. This involved looking at several categories of mapped waypoints: waypoints connected by the HM team to a HM lesson, waypoints connected by the CM team to a CCSSM topic, and waypoints included by the CM team in a neighbourhood map for a CCSSM topic area.
Enlarge…
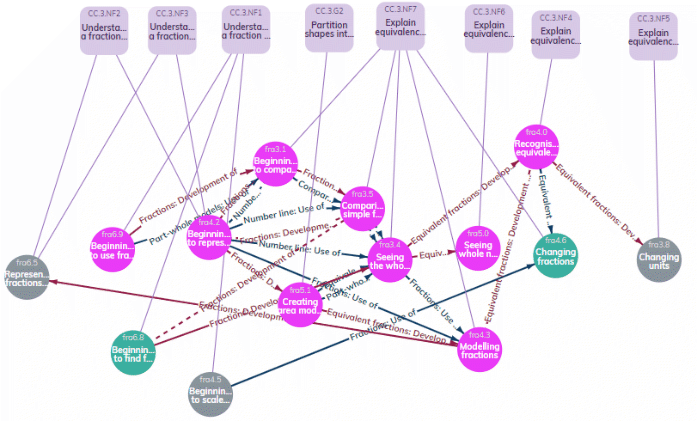
Overall, the CM team constructed nine types of saved searches, which were then shared with the HM team. An example is shown in Figure 4, where the upper layer of nodes (curriculum nodes) represents the statements taken from the CCSSM (light purple squares) or a HM lesson (bright pink). These are connected to the waypoints (in this case, only green and grey). Colour coding of nodes allowed for a quick reference of the categories.
The types of mappings that were found useful included:
- mappings which highlighted differences between the nodes identified by each team,
- multi-grade mappings identifying differences in the grade-level ordering of the CCSSM/HM when compared to the suggested pathway in the CMF.
- mappings from perspectives of minimal and/or neighbourhood viewpoints,
- neighbourhood mapping for the CCSSM content with the HM lessons in their expected teaching order to help evaluate the teaching order of the lessons and the content upon which they rely with respect to the CCSSM for the same grade.
Outcomes
Outcomes for the HOTmaths team
By expanding the maps, using a simple double-click on the identified waypoints, the tool enabled the HM team to identify the waypoints (from fractions content) that were not assigned to any lesson, and to expand each map to include interlinking waypoints from related concepts outside those designated as pertaining to “fractions”. These additional waypoints were instrumental in identifying additional material, concepts and learning activities needed for the lessons.
The longitudinal maps created by the CM team mapped multiple grades of the CCSSM. They provided the HM team with some validation of their unease about what seemed to be age-inappropriate or misplaced material in some grades of the course. The mapping showed that sequencing in the CCSSM varied significantly to that of the established HOTmaths lessons. However, the versatile material presented in the waypoints provided the HM team with some student activities and teaching strategies to help overcome these issues.
A key outcome for the HM team was that they were able to identify issues with the flow of the CCSSM requirements, and where additional material was required. Suggesting additional material initially caused some issues with the client, but the Framework helped to justify this. HM then could rearrange material and introduce interlinking material. According to colleagues from the HM team, “by working with a reputable team like Cambridge Mathematics, it legitimised our content in the eyes of the stakeholders” (HOTmaths team member, personal communication, August 8, 2022).
The mapping helped HM identify some waypoints that were not sufficiently addressed in their existing material for HOTmaths students, and suggested what additional material could cover these concepts. For example, the HM team decided to include in their own material the student actions from waypoint fra3.8 shown in Figure 5.
Category: Procedural Fluency - Performing
Recognise that by changing the length reference unit, equivalent fractions can be generated, for example: 30cm can be written as 300mm, this can be explored through considering the metre unit, consisting of 100cm or 1000mm, 30cm could be represented as 30 out of 100 in cm or 300 out of 1000 in mm.
Find other examples in currency, weight, capacity.
In summary, the project helped the HM team to legitimise their content in the eyes of key partners and reflect on the mathematics content they were developing:
Even when material is being developed by experienced teachers, some critical learning experiences may be missed. The framework allows developers to not only confirm their own understanding of how mathematics is best learned, but also provides an expert bank of detailed ideas they may have not considered. Having this reliable and comprehensive framework of mathematical learning provides support for both teachers and material developers.
(HOTmaths team member, personal communication, August 8, 2022).
Outcomes for the Cambridge Maths team
The CM team mapped the CCSSM curriculum to the framework both by grade and longitudinally across the grades. These maps were then compared to the HM lesson maps to form an overall picture of the extent to which the HM lessons contained all the concepts from the CMF.
For the CM team, this project enabled them to have hands on, practical exploration of the functionality of the Framework and how the Framework can be used to support specific requirements of others. In this case, the CM team wanted to use the Framework to compare different constructs (the CCSSM and HM lessons). This led to the development of data groups, which enabled users to apply colour codes in various ways to group concepts together. Data groups allow waypoints to be identified (through filtering and visualisation) from multiple perspectives, for example to distinguish the HOTmaths content and the CCSSM content. This is a useful addition to the functionality of the Framework.
The mappings identified areas where the existing trajectories in the CCSSM and the Cambridge Mathematics structure differed. It prompted the team to revisit areas and ensure that decisions were justifiable and evidenced in the research. Upon discussing these contradictions with the HM team, the CM team were able to refine their own language and explanations as well as cement the idea that CMF is one ‘map’ of many, and it may be adapted and refined to suit a variety of contexts and priorities.
Working with the HM team also enabled the CM team to prepare for future mapping projects with other partners. Various issues arose during the training and mapping process, as each week, the HM team’s observations and queries were addressed. This enabled the training program to be refined. For example, some aspects of the Framework needed more clarification than expected, such as the difference between nodes and waypoints and the numbering system being used. These were easily addressed by the CM team. The help sheets created by the CM team have been used in other projects since and have been found to be highly valuable when users need a reminder of how to interact with the Framework. Some aspects of the functionality needed improvement and are being changed, including protection from accidentally deleting waypoints and viewing waypoints in table format. The HM team also raised a small number of issues about the substantive content of the Framework which led to review by the CM team. Specific amendments to individual waypoints were carried out immediately in light of feedback from the HM team. The CM team greatly valued the interaction with the HM team, which improved the waypoints. See the report by Majewska (2021) for further details.
Discussion
How the CMF can be used by others to inform their work?
The CMF has been and can be used by other professionals in various projects, including mapping curriculum objectives to the Framework to analyse gaps or evaluating if material flows in a coherent manner. Users of the Framework can map their material to the CMF or map the CMF to their material. It is a multi-step process. Firstly, those evaluating their materials would need to identify nodes they would like to map. They would need to decide on what these nodes represent (e.g., curriculum statements) and could then map from these new nodes to waypoints in the Framework, reflecting as they progress. They would then need to explore the waypoints that have been mapped to and consider if they are connected, or if they are disjointed in any places. They may need to consider if there are waypoints that could be added to create a more connected/coherent collection. Finally, they could use this process to reflect on how this may impact the original content being evaluated.
There are some cautions for potential users. Firstly, creating such mappings is very much context specific. This means that mappings are only relevant to the immediate context. In this case, the fraction mappings could not be applied to another context, even if it related to the same grades. Constraints of context mean that mathematical experiences cannot follow the CMF strictly. For example, in the CCSSM, fractions perceived as division happens to be located much later than it is represented in the Framework, so this restricts the pathways through the content. The CMF, however, does help to make informed decisions and can help designers in recognising the implications of these decisions. Another consideration is that the process of using the CMF to map content is time consuming and requires reflection and solid understanding of the context being mapped. The CMF is also only one of many potential representations, showing progressions we have identified from research and evidence that we have access to. There are important limitations, such as using only English-language research.
Recommendations
Not only was this an opportunity for the CM team to receive feedback about the design, content, and functionality of the Framework, but this collaboration also provided a significant amount of direction for introducing and familiarising external teams with the Framework and what it can do. The CM team learned valuable lessons and benefited from collaborating with the HM team, demonstrating the importance of joint working, as noted by McKenney and Reeves (2012). The HM team also benefited in many ways. A team member wrote that “the Framework was an invaluable tool for identifying the intricacies of learning and understanding mathematics: the steps, the flow, the concepts, the student experiences and the way mathematics topics interact” (HOTmaths, personal communication, August 8, 2022).
The co-operative, collaborative nature of the project enabled the CM team to truly appreciate the value of working together on developing educational materials and on how the Framework offers not an answer, but a structure against which informed decisions (and their consequences) can be made with regards to curricula.
The project demonstrated that the Framework can be used to find disjointness and unify curriculum content (e.g., fractions lessons in this instance). The Framework offers a structure that is flexible enough to be used by different professionals and communities, yet robust enough to maintain mathematical connectedness and coherence to give that unifying structure.
It is of interest to see what the long-term outcomes of this project may be. Could the new HM lessons improve HOTmaths students’ understanding of fractions? Do the changes support teachers who deliver the lessons? Could the mappings support practitioners in classrooms? Although the answers to such questions would require further (possibly longitudinal) investigations, it would certainly be worth exploring what the outcomes of our collaboration may be.
References
Cambridge Mathematics. (n.d.). Key terms in Framework documentation. https://www.cambridgemaths.org/research/key-terms-in-framework-documentation/
Common Core State Standards Initiative. (n.d.) Common Core State Standards for Mathematics. Retrieved from https://www.nctm.org/ccssm/
Jameson, E. (2019). Methodology: Building the research base. Cambridge Mathematics. https://www.cambridgemaths.org/Images/methodology-building-the-research.pdf
Jameson, E. (2020). Mapping MathemaTIC tasks to the Cambridge Mathematics Framework. Cambridge Mathematics. https://www.cambridgemaths.org/Images/mapping-mathematic-tasks.pdf
Jameson, E., & Horsman, R. (2020). Using the Cambridge Mathematics Framework to refine the UNICEF-Cambridge Curriculum Progression Framework (Mathematics). Cambridge Mathematics. https://www.cambridgemaths.org/Images/unicef-cambridge-curriculum-progression-framework.pdf
Johnson, M., Horsman, R., & Macey, D. (2021). Design for learning in uncertain contexts: Developing maths concept sequences for emergency situations. Educational Designer, 4(14). http://educationaldesigner.org/ed/volume4/issue14/article55/
Jameson, E., Horsman, R., Macey, D., Gould, T., Rushton, N., Rycroft-Smith, L., Majewska, D., Stevens, B., & McClure, L. (2020). Ontology: Structure and meaning in the Cambridge Mathematics Framework. Cambridge Mathematics. https://www.cambridgemaths.org/Images/ontology.pdf
Majewska, D. (2021). Case study report: Using the Cambridge Mathematics Framework to map the Common Core to HOTmaths: A summary. Cambridge Mathematics. https://www.cambridgemaths.org/Images/hotmaths-case-study-a-summary.pdf
McKenney, S. & Reeves, T. C. (2012). Conducting educational design research. Routledge.
NCTM. (n.d.). Common Core State Standards. https://www.nctm.org/ccssm/
Swan, M. (2014). Designing tasks and lessons that develop conceptual understanding, strategic competence and critical awareness. Tarefas Matemáticas: Livro de Atas Do Encontro de Investigação Em Educação Matemática, 9–28.
Swan, M. (2015). Professional Development and Cambridge Maths [PowerPoint slides]. Cambridge Assessment. https://www.cambridgeassessment.org.uk/Images/cambridge-mathematics-presentation-prof-dev-malcolm-swan.pdf


