Building Mathematical Spaces Through Multi-Faceted, Body-Scale Geometry
Abstract
In the course of conducting educational design research, new learning activities may emerge, sometimes serendipitously, that resonate with educators’ intuitive understandings of what learning could and should be like. Articulating these activities’ ‘secret sauce’ could enable the creation of similar educational activities. This article examines one such activity from mathematics education research, the Embodied Icosahedron activity, which numerous practitioners have described as an ideal mathematics learning experience. To characterize the activity’s appeal, we first document how this activity was disseminated across education research, teacher education, professional development, classroom, and community settings. Next, we present and analyze interviews with educators who facilitated the activity in each of these educational contexts. At the intersection of these multiple testimonies, analysis reveals, is a shared appreciation of three design qualities: body-scale movement, authentic embedding of disciplinary content within an activity, and realizations of constructionist pedagogical philosophy. The realization of these qualities within a mathematics activity - a domain renowned for its reputation as abstract, impersonal, and boring - suggests a particularly promising approach to educational design. To achieve inclusive, empowering mathematics education, we speculate, we should pursue the design of authentic tasks at the intersection of mathematics and existing practices that already engender those types of transformative interaction.
Introduction
Imagine a mathematical activity that spontaneously attracts learners of all ages and backgrounds, from toddlers to university faculty. It is equally appealing in settings both formal (e.g., classroom lessons and university lectures) and informal (e.g., regional fairs, community gatherings). This activity lives and breathes the constructionist commitment to ‘low floors, high ceiling, wide walls’, with learners exploring concepts as foundational as counting and properties of a triangle, and as advanced as the cross-sectional areas of an icosahedron and the duals of platonic solids. As learners work on this activity, their self-generated questions abound: “Why didn’t that work?”; “That didn’t do what I thought it would—what’s going on?” Imagine, too, that this activity’s materials cost less than $75 USD, can be assembled for use at home in less than 1 hour, and can be reused indefinitely.
Certainly, educators might wish that such captivating mathematics activities were commonplace. Unfortunately, the activity described above sounds magical precisely because it embodies features that modern curricular materials tend not to engender very well. When we stumble upon such experiences, can we derive from them some principles, some elements that constitute their ‘secret sauce?’ To make more of these activities, one might surmise, we first need to capture what it is about them that makes them so special to multiple stakeholders in mathematics education, and perhaps what features allow them to traverse the typical boundaries both of personal interest (i.e., ‘math people’ vs. ‘non-math people’) and curriculum silos (i.e., preschool, elementary, secondary, upper-division math, etc.).
To probe issues of design and theory pertaining to mathematics learning activities that captivate diverse audiences, this reflective paper evaluates the design and dissemination of one example activity, the Embodied Icosahedron (Ico for short). This relies on collaborative body-scale movement to construct and investigate a polyhedron composed of twenty congruent equilateral triangles (Figure 1). We situate this particular example within literature on body-scale movement, embodied mathematics, and constructionism to characterize what makes this activity unique. We then report on results from qualitatively analyzing interviews with 5 educators who implemented Ico, to identify structural, functional, and social features apparently contributing to its broad popularity. Three of the interviewees are also authors of this paper. Interpreting these interviews through the aforementioned theoretical lenses, we generalize tentative implications for the design of mathematics learning activities. Findings from this study surface some often-overlooked constructionist tenets that, were they more widely adopted, could perhaps better serve mathematics teachers and learners.
Example Design: The Embodied Icosahedron

Enlarge…
The full Embodied Icosahedron Activity (Abrahamson & Rosenbaum, 2016), which we first ran in a working group on embodiment at the 2016 annual meeting of the North-American Chapter of the International Group for the Psychology of Mathematics Education, includes 7 construction stations, step-by-step instructions, and a discussion guide. Discussion questions focus on properties of the icosahedron, including: number of vertices, edges, and faces; cross-sectional areas (e.g., “If the icosahedron were balanced on one vertex and half filled with water, what would the shape of the water’s surface be? What if the shape instead rests on a face?”); and geometrically related shapes (e.g., “What is the dual of the icosahedron, that is, the shape formed by connecting all the center points of each face?”). The full set of construction stations (Figure 1) includes: paper nets, toothpicks and foam balls, magnetic rods and balls, wooden dowels and plastic tubes, and snap-together triangles. Each station also includes a 20-sided die, the smallest scale of icosahedron presented. Thus, participants can construct the icosahedron at scales ranging from hand-held to larger-than-body-size and in both wire-frame (e.g., the rod-and-dowel constructions) and solid forms (e.g., the die and paper nets). Though educators who have run this activity have varied the particular stations present, the large wooden-dowel station (Figure 1, bottom centre) was always present.






Top row: Paper nets, toothpicks and foam balls, magnetic rods and balls.
Bottom row: Snap-together triangles, wooden dowels and plastic tubes, detail of plastic tube joints.
In facilitated settings (e.g., university lectures), the full Embodied Icosahedron typically lasted 45-90 minutes with 8–45 participants. The exact programming and number of stations vary by context but typically include an introduction to the icosahedron as a shape (displaying and pronouncing the word, sharing examples from daily life), an introduction to ideas of embodied cognition (typically described as “using physical objects or experience to reason about math”), an invitation to select a build station, rotation through the build stations about every 20 minutes, and a concluding whole-group discussion. Often, participants gather by the largest icosahedron as they finish work at other stations. Subsequent group discussions almost always focus on the largest icosahedron build.

Enlarge…
In less facilitated settings (e.g., community fairs, family nights), materials for the largest icosahedron are often presented alone with a prompt to “see what you can build.” Informal facilitators may create sample builds, often at a smaller scale, to prime learners’ imaginations yet refrain from giving specific instruction. Informal learners participate in ways and duration of their choosing, typically without any summative discussion.
Though not a focus of this paper, we note that Ico’s design has inspired some closely related variants within the long history of using flexibly joined dowels for geometric constructions. Using an eye-hook and ring design (Figure 2) allows for more generalized geometric construction, including tetrahedra, octahedra, and free collaborative sculptures. Our own original activity and variants have been implemented more than 25 times with more than 75 educators and hundreds of learners. Given the popularity of the largest icosahedron among both learners and facilitators, the remainder of this article focuses on the activity around that structure, which we refer to as Ico.



Top left: eye-hook and ring mechanism; bottom left: tetrahedra and octohedron (photo: Alexander Refsum Jensenius); right: abstract collaborative sculpture
Historical Origins and Theoretical Foundations of Ico Design
Given Ico’s full-body movement, mathematical topics, and activity style, we situate this activity within three research literatures: traditions of dance and body-scale movement in icosahedra, embodied cognition for mathematics learning, and constructionism. While the first of these literatures primarily will offer historical and theoretical context, we later use embodied mathematics and constructionism as lenses through which to analyze educator interviews.
Dancing icosahedra and body-scale movement
When we move, we move in space. While in some sense trivial, this statement becomes interesting once we both accept movement as the phenomenological crucible of intelligence (Allen & Bickhard, 2013; Piaget, 1971; Sheets-Johnstone, 2011; Varela et al., 2017) and recognize educators’ agency in shaping spaces of movement to bring about particular forms of motor learning (Adolph et al., 2018; Reed & Bril, 1996). When we shape space, we constrain movement and, therefore, we create motor problems whose solution promotes the development of targeted skills (Araujo & Davids, 2004; Feldenkrais, 1981; Orth et al., 2017). Typically, learners solve motor problems through developing new perceptuomotor competences (Duijzer et al., 2017) centered on emergent ontologies that they come to discern in the activity space (Hutto et al., 2015; Tancredi, et al., 2022). These new forms that students perceive can in turn become the cognitive basis for learning mathematical concepts (Abrahamson & Trninic, 2015; Alberto et al., 2022).

Enlarge…

The relationship between space and movement, which is implicitly foundational for all dancers, has fascinated choreographers, some of whom have sought to systematize the relationship as a generative creative methodology. Notably, American choreographer William Forsythe developed a movement style involving actual or imaginary geometric forms, such as a rectangle, that constrain movement possibilities, giving birth to new motor solutions. Forsythe “often connected ballet to mathematics and said that ballet is ‘a geometric art form,’ that a dancer is ‘taught to match lines and forms in space’” (GrandpaSafari, 2008). A century earlier, Rudolf von Laban (b. 1879) had laid the intellectual foundations for a movement-oriented philosophy of space oriented on characterizing modes of physiological efforts. Laban expounded on his spatial theories of movement by having dancers enter into the hollow of a human-scale icosahedron and move along its multiple axes [1]. Figure 3 shows the dance scholar and movement director Ami Shulman demonstrating Laban poses in an icosahedron constructed at the RITMO workshop, Summer 2022. Learning scientists interested in the relations between perception, action, and cognition continue to be inspired by the potential of artifacts, space, and movement to occasion mathematics learning (Abrahamson et al., 2011; Kelton & Ma, 2020; Nemirovsky et al., 2013; Rosenbaum et al., 2020; Vogelstein et al., 2019). Specifically, the icosahedron will here be discussed as a catalyst for mathematical insight (Abrahamson & Rosenbaum, 2016; Palatnik, 2022).
Embodied cognition and mathematics
Theories of embodied cognition maintain that cognitive processes are rooted in, and rely upon, sensorimotor experiences of the world, with “[s]ensorimotor simulations of external situations [being] widely implicated in human cognition” (Wilson, 2002, p. 633). Extensive research in developmental psychology connects motor development to mathematical reasoning. With kindergarten-aged students, development of fine motor skills is linked to fluency with finger counting (Fischer et al., 2018) and predicts mathematics achievement on current and later standardized tests (Dinehart & Manfra, 2013; Grissmer et al., 2010; Luo et al., 2007). Among elementary school children, motor proficiency is positively correlated with cognitive ability and academic achievement generally (Cadoret et al., 2018; Fedewa & Ahn, 2011) and in mathematics specifically. Students trained to move in pedagogically relevant ways when learning about angles were found to out-perform their control-group peers (Shoval, 2011). And across age groups, gesture has been implicated as an important, movement-based resource for mathematics teaching and learning (Alibali & Nathan, 2012; Arzarello et al., 2005, 2009).
Inspired by these theoretical developments, practitioners of embodied design seek to create environments and activities that target disciplinary content by fostering connections between learners’ actions and perceptions (Abrahamson, 2009). Among such works is a genre of full-body immersive learning environments, in which learners can experience and subsequently generalize central concepts from STEM fields (Malinverni & Pares, 2014). Researchers have been interested in the pedagogical potential of large-scale full-body movements that engage the spine and core, induce disequilibrium or locomotion, and require coordination with others (Knoll et al., 2015). These activities are distinct from the more common activities involving small-scale movements of only the eyes, wrists, and fingers; and distinct from medium-scale activities involving full-arm movements yet without displacement of the core or spine (Gerofsky, 2010, 2011). We situate Ico within the family of full-body mathematics learning designs (see the section Related Works for further design examples).
Constructionism
Ico is essentially a learning-by-building activity. As such, it is worthwhile to examine how this activity relates to themes from a pedagogical approach explicitly founded on construction, namely, constructionism (Papert, 1980). Constructionism “adds the idea that this [knowledge building] happens especially felicitously in a context where the learner is consciously engaged in constructing a public entity, whether it’s a sand castle on the beach or a theory of the universe” (Papert & Harel, 1991, p. 1). Constructionism has been widely influential within education research and design, informing both cross-cutting theories of cognition and situated knowledge (e.g., Cavallo, 2000) and educational practices (in computer science, design-based learning, makerspaces, etc. – Blikstein et al., 2016). As we detail below, constructionist principles are manifest in three aspects of Ico: pedagogy, epistemology, and design.
Within mathematics pedagogy, specifically, Papert (1980) proposes three principles for constructionist mathematics activities: content should be experienced as continuous, in that it builds on learners’ prior knowledge, skills, and experiences; learning mathematics should give learners the power to accomplish meaningful, previously out-of-reach tasks; and the accomplishments of mathematical work should be culturally resonant, in that they are implemented in familiar genres and forms and appreciated by learners’ broader communities. In our analyses, we aim to document how Ico embodies these principles.
Constructionism also elevates certain often-overlooked epistemologies. Though far from the first theory to emphasize the role of externalizations in learning (e.g., Vygotsky’s entire research program on tools, language, and interpersonal interaction), constructionism departs from constructivism and socio-cultural perspectives in that it maintains a commitment to the role of the concrete not only as a first stage of learning, on which to base subsequent abstraction, but as a constant presence throughout work and learning. Constructionism celebrates the situated, concrete, bricoleur approach as a legitimate epistemology throughout life (Turkle & Papert, 1991). Papert’s LOGO environment enabled — and his pedagogy encouraged — a more fluid, give-and-take approach to computer programming. It created avenues for learners to engage with elements of logic, geometry, spatial reasoning, and control mechanisms in ways more typically associated with the arts than engineering, recasting those elements to learners who might prefer the former. Importantly LOGO, and other activities inspired by it, do not preclude a more step-by-step, top-down approach. Instead, they support both systematic and bricoleur approaches as well as a combination thereof.
Finally, other constructionist scholars argue for designs that encourage learners to adopt varied, fluid positions relative to their work. Inspired by Kegan (1982), Ackermann (1996, 2001) proposed that the deepest learning experiences result from a cyclical ‘dance’ between immersion (‘dwelling in’ the concept) and distancing (‘stepping back’ to reflect). Through such a process, learners coordinate between elements of immersive and removed perspectives, identify invariants, and negotiate discrepancies, thus achieving deeper understanding than offered by either perspective alone (see also Benally et al., 2022). Despite research suggesting its value (Gerofsky, 2011), dwellable mathematics activities remain relatively rare, with most representations being small relative to learners’ bodies and on 2-dimensional paper or screens. In developing Ico and investigating the learning opportunities it creates, we aim to elaborate on the constructionist principles and modes of thinking enabled by physically dwelling in mathematics.
Related Works
We situate Ico within a family of full-body mathematics learning designs (e.g., Kelton & Ma, 2020; Walkington et al., 2019). A branch of this family tree includes the construction of body-scale (or larger) mathematical structures through collaborative inquiry, coordination, and negotiation as in Walking Scale Geometry (Ma, 2017), dancing math (Rosenfeld, 2017; Vogelstein et al., 2019), video tessellations (Mickelson et al., 2011), and a giant etch-a-sketch (Nemirovsky et al., 2013). In another subset, designs allow for flexibility in this coordination as learners step in and out of group work, enabling both independent and coordinated action such as in Walking Scale Number Line (Ma, 2017), the original LOGO turtle robot (Papert, 1980), Geometris (Durán–López et al., 2017), and motion tracking or GPS graphing (Arzarello & Robutti, 2004; Hall et al., 2015; Nemirovsky et al., 1998). However, with few exceptions such as the Walking Scale Number Line, these designs require costly or custom-built hardware systems, potentially limiting their dissemination to those with either the financial resources to purchase them or the DIY confidence to construct them from scratch. In documenting the development, dissemination, and reception of Ico, we aim to highlight design features that enabled body-scale, constructionist mathematics in a low-cost, non-digital, easily replicable activity.
Research Goals
Ico was a serendipitous design, born out of an embodied-design research group’s inquiry into the history of choreographic philosophy. Yet now that Ico exists, we would like to determine its inherent qualities that promoted its uptake as an engaging popular activity. Thus, to support the development of other affordable, body-scale, constructionist learning activities, particularly in mathematics education, this article aims to:
- Document the spread of Ico and its variants to understand which features enabled and supported this spread; and
- identify the features of Ico that contributed to its appeal.
Methods
We first introduce the five educators interviewed for this study. We then outline the data collection procedures and analysis techniques.
Interviewees
Two of the educators who were interviewed for this study were pre-school teachers and the other three were authors of this paper with experience implementing Ico. We analyze interviews with these five educators to identify features of Ico that contributed to its popularity and spread.
Dor Abrahamson, the last author on this paper, is a professor of education, and his research and teaching focus on embodied cognition and educational design, specifically focusing on mathematics learning. Since first implementing Ico with Leah Rosenbaum in Fall 2016, Dor has run Ico in university courses serving pre-service STEM teachers as well as at research conferences.
Alik Palatnik, the third author of this paper, is also professor of education, and his research interests include embodied learning and design as well as geometry teaching and learning. After participating in Ico at a research conference, Alik implemented it in university courses as well as with in-service teachers. He also designed a variant activity involving the construction of a tetrahedron and octahedron at various scales.
Paul Reimer, the second author, is the director of a non-profit organization focused on early math and science education, where he works to develop research-practice partnerships focused on collaborative design for playful, participatory engagement in mathematics and science education. After participating in Ico at a research conference, Paul implemented it in a community Maker Faire as well as in professional development (PD) workshops with 100+ preschool through to grade 2 teachers.
Ms. Williams and Ms. Clark [2] participated in one of Paul’s teacher PD workshops in Summer 2019. They subsequently built kits and used them with their preschool students in Fall 2019 and Summer 2020. They also ran Ico as part of a professional development seminar that they led in Fall 2019, reaching other early childhood educators in their community.
Data Sources & Analysis
Since its design in Fall 2016, Ico has been implemented over 45 times by more than 30 different educators with hundreds of learners. Five of these educators served as the participants of this study and offer indirect access to their students’ experiences with Ico. Dor, Alik, Paul, Ms. Williams, and Ms. Clark were individually interviewed by the first author using a semi-structured interview protocol that addressed the following topics:
- how the educator learned of Ico;
- the audiences and contexts with which they implemented it;
- what the educator hoped their students would learn from it;
- modifications the educator made to Ico to better fit their students; and
- patterns or interactions the educator noted as remarkable within their students’ work.
When possible, educators were asked to elaborate their interview responses with examples. These interviews were video recorded using Zoom, and the automated transcription was verified by the first author to produce a written transcript.
Through a grounded coding process (Chong & Yeo, 2015), the first author identified the 12 initial codes that appeared across the five interview transcripts (Table 1). Through discussion with all authors and inspired by nexus theory (Peppler & Wohlwend, 2018), these themes were clustered and attributed as practices of three areas: body-scale movement, mathematics, and constructionism.
|
Final Areas of Practice |
||
|---|---|---|
|
Body-scale Movement |
Constructionism |
Mathematics |
|
Large Scale 3D structure Unfamiliarity Movement |
Collaboration Construction Emotional response Multiple ways of knowing |
Perspective taking Expressing math materially Geometric reasoning Spatial reasoning |
Results
We first document how Ico spread across diverse education contexts, including academic education research, teacher education, professional development, classrooms, and community settings. Drawing on our findings from the interviews, we then present features of the activity that, we believe, contributed to its popularity and spread. We characterize these features as emerging from a convergence of three design inclinations embedded in the activity’s design: body-scale learning activities, authentic embedding of mathematical content within the activity, and constructionist pedagogical philosophy.
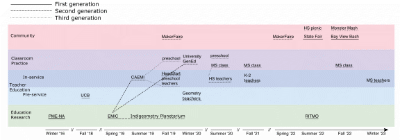
Enlarge…
Implementation across diverse educational settings
To highlight how Ico spread across different mathematics education contexts and served mathematics teachers and learners of varying backgrounds, we present a timeline of when and where this activity was developed and implemented (Figure 4).

In Spring 2016, Dor constructed the body-scale Ico in the Embodied Design Research Laboratory (EDRL) at the University of California, Berkeley as part of an investigation into the history of dance philosophy and choreographic notation. Lab members were intrigued by the inherent geometric features of the structure, and so an idea emerged that perhaps this solid could serve in supporting mathematics students’ content learning. The first three public implementations outside of the EDRL were conducted by Dor and Leah in academic settings: two conferences and a pre-service teacher education course.
Participants in these first implementations then spread Ico to other contexts. Having participated in one of the early academic conferences, Paul then ran Ico at three PD workshops and a community Maker Faire. Alik, who also experienced Ico at an academic conference, also implemented it in two separate pre-service teacher education courses and an in-service teacher PD event. Further, one of Dor’s doctoral advisees modified the largest icosahedron construction and implemented it with Indigenous children in the southwest US (see Benally et al., 2022).
Participants from these implementations started running Ico in their own contexts. Ms. Williams and Ms. Clark, who were part of Paul’s PD workshops, ran the activity in their preschool classrooms in Fall 2019 and in a PD workshop for fellow preschool teachers. The high school teachers who participated in Alik’s in-service PD event then ran Ico for hundreds of middle school students shortly thereafter. Figure 4 illustrates how the Ico continued to spread across academic, teacher education, classroom, and community settings, facilitated both by the authors as well as by participants of earlier Ico events.
Emergent practices and pertinent features
Having documented above the development and spread of Ico, we next analyze the interviews. We identify common practices that appeared across implementations and attribute those practices as emerging from three areas: body-scale movement, mathematics, and constructionism. In discussing each area, we aim to illustrate the ways in which Ico participants engaged in practices germane to that area.
Body-scale movement practices of space-taking and space-making
Fulfilling the designed intention, interviewees experienced Ico as a full-body activity negotiated between participants and with the surrounding environment. As facilitators, they noted the range of sensory experiences elicited by the activity (Table 2). Practices of space-taking and space-making also emerged as salient as participants altered their typical surroundings to accommodate this work (Table 2). Once delineated by the icosahedron, those spaces seemed to take on new, often emotional meaning (Table 2). Finally, construction and exploration of the shape gave rise to new coordination patterns both with the physical materials and with other participants, with facilitators highlighting spatial, linguistic, perspective-taking, and role-taking work among participants (Table 2). With its scale and materiality, the large icosahedron created attractive opportunities for body-scale movement practices of sensory experience, space taking and making, and coordinating movement.
|
Practice |
Examples |
|---|---|
|
Sensory experience |
University: "The feel of these rods in my hand and the possibility to grasp the vertex, for instance. It was almost a different tactile and a moving experience for me." Teacher PD: "The variety of sizes was good ... for bodily engagement. ... And you can already see as people moved over there, there were some people stretching." |
|
Space Taking & Space Making |
Teacher PD: "So the large scale, the fact that we had to move tables and move chairs and you're going to have this whole space here." Pre-school: " … our director kept on coming in and just sitting in the icosahedron, said, ‘This is my space.’ She was calling it ‘my crying icosahedron’ cause she was a little stressed. So she’s coming in and sitting in this space, and for her and the adults, it was becoming this social emotional space where she was able to kind of feel herself in that space and, of course, all of us teachers were doing the same thing, just sitting in the icosahedron. That was our moment." |
|
Coordinating Movement |
In spacePreschool: “[one student] had a plan [to roll the ico] and then when she got to me, I think she realized that it was gonna get too close to me ... And so she goes backwards to try to move it the other direction cause this is big, and ‘How do I keep a safe space or distance from someone else without bumping into it?’ I think that was probably part of her thought process of how it moved within our yard.” With other peoplePreschool: “But as we first started to build it, it was more of just a dome shape where it was on the ground. And then as it continued to grow, the more friends that they could put inside of it, the more friends try to move it, the quicker it comes apart.” Preschool: “And I could’ve given them a heads up around, ‘If you’re going to move it, we need to make sure that one person is moving it at a time.’” University: "Natural switching of the roles. So one is constructing and then the other is taking this model. ... So there are some roles there in this construction process but they are not too strict and this activity evolves very naturally." |
|
Math Area |
Math Practice |
Examples |
|---|---|---|
|
General |
Defining vocabulary |
Teacher PD: "I did have everyone pull up an icosahedron on their phones or smartphones, just to see a picture of what the figure looked like.” Pre-school: "And icosahedron became a word in their vocabulary, too." |
|
Counting |
Teacher PD: “So counting the number of triangles. Counting the number of vertices. Counting the number of dowels that were needed to construct it.” Pre-school: “And then you really have to count. Do you have 5?” University: “Just to count what is a given, it will go to good strategy.” |
|
|
Geometric Reasoning |
Construction |
University: "I think it's related to the very pragmatics of building. ... We actually cared about this obscure geometric question of how many edges does an icosahedron have because we needed to build it." Teacher PD: "And you uncover the properties as you're building it. Oh, all these rods have to be the same length. Oh, okay. What if they aren't the same length?" |
|
Composition of shapes |
Pre-school: "'Oh look, this is triangles, right? It’s creating this larger shape.’ And so we talked about that a little bit." Teacher PD: "In terms of the icosahedron itself, thinking about a variety of different structures within the larger shape itself." |
|
|
Similarity |
University: "She took this hand-sized model and she almost brought it inside the structure which is under construction. … this issue of similarity is central ... we talk about similar triangles, but we never talk about similarities of solids." |
|
|
Spatial Reasoning |
Orienting in space |
University: "They were aware of the importance of how you position the icosahedron. [...] And in their opinion, to position it on the vertex and it gives you a much better understanding of the shape." University: "The question was how many edges are there? [...] they rotate and then immediately they saw, 'Oh. It's the structure from the bottom, identical one from the top and then crissey-crossey-crissy-cross in the middle.'” |
|
Moving in space |
Pre-school: "She’s already figured out in the short time that she was exploring it, that if she pushed the other side, that one would come down." |
Mathematics practices
Working with the icosahedron pushed participants, from preschoolers to university students to seasoned teachers, to enact a range of situated mathematical practices (Table 3). Some of these practices were general, such as defining, counting, and argumentation. Other practices - such as (de)composition of shapes, considerations of similarity, and reasoning about cross-sectional shapes and geometric duals - addressed the icosahedron’s geometry. Still other practices focused on the shape’s position and movement in space, engaging spatial-reasoning concepts of perspective-taking, orientation, and movement. Given the prominence of these practices in national guidelines (National Governors Association Center for Best Practices & Council of Chief State School Officers, 2010; NCTM, 2000), we argue for Ico’s pedagogical utility in authentically engaging participants in these practices.
Constructionist principles, approaches, and “dwelling in”
Interviewees’ reflections suggest Ico also exhibits Papert’s principles of mathematical continuity, power, and cultural resonance. A degree of continuity can be inferred from participants’ facility in engaging with Ico’s familiar materials (i.e., knowing how to work with wood dowels and plastic tubing from having encountered such materials before). The activity also made the interviewees as facilitators re-evaluate their own understanding of an icosahedron and, in many cases, their presumed mastery over the shape’s geometric properties (Table 4, Continuity). In accordance with the power principle, educators noted that they “actually cared about this obscure geometric question of how many edges does an icosahedron have because we needed to build it" (Table 4), bringing relevance and consequence to the shape’s geometry. Finally, the activity resonated with participants’ broader lives, as evidenced by their eagerness to share it with others (Table 4). Compared to Papert’s LOGO, Ico has more limited opportunities for expression and prolonged engagement, at least as currently designed. We nonetheless take these interactions and reactions as evidence of enacting similar mathematics pedagogy principles.
Across implementations, participants also exhibited both top-down and bricoleur approaches to the Ico construction task (“Some groups have followed the directions quite closely [...] Other groups just sort of started to, like, oh, let's try to build this," – Table 4) though, admittedly, to the same, pre-defined end product. Thus, Ico seemed to open multiple ways of knowing and reasoning about geometry and space beyond the step-by-step approach through which these concepts are typically met. Finally, educators highlighted the opportunities Ico presented to dwell in mathematics (Table 4) and commented on how participants across age groups appreciated these opportunities.
|
Practice |
Examples |
|---|---|
|
Continuity principle |
University: “So I know what an icosahedron is. [..] So I started immediately to connect stuff and because I have this in my mind. [...] But suddenly, I realized that it’s not closing on itself, because we somehow as a group messed it up. [...] It was not disappointing, but it was strange. ‘Wow, how could I mess this up because I know this thing?’” PD: “I found that even my own perception of the figure and coming into it in different stages of construction and in different sizes. It’s like, oh, ‘I thought I knew this. But no, I still don’t understand some of what makes this thing come together.’” |
|
Power principle |
University: "We actually cared about this obscure geometric question of how many edges does an icosahedron have because we needed to build it." Teacher PD: “And you uncover the properties as you're building it. Oh, all these rods have to be the same length. Oh, okay. What if they aren't the same length?" |
|
Cultural resonance principle |
Teacher PD: “So when I see people building this and then coming together and there are high fives. There's cheering. People are posting this on their social media.” University session ended with the group striking a pose in the icosahedron for a photo. |
|
Epistemological pluralism |
University: "I want them to experience mathematics in new ways." Teacher PD: "I thought this might have been an important tool or an activity in professional development to really focus on expanding ideas about ways of knowing in mathematics. So, knowing through experience. Knowing through construction and knowing through bodily interaction with this. [...] But like that this was an important way for them to understand that they know things through their experience." Teacher PD: “Some groups have followed the directions quite closely when it came to building the tabletop and the large scale, and even with the, with the magnetic rods and balls. So building that followed directions. Other groups just sort of started to, like, oh, let's try to build this." University: “So first of all, they started to construct, and they did not plan to do, like, "okay let's count the edges" or "let's count the vertices" or even "let's understand what happened here to discern." So first of all, they just started, ‘Okay let's, let's put these rods together’ and so forth.” Preschool: “Yeah, we’re building this shape! [...] Yeah, let’s see what we can create!” That’s kind of my teaching style, I guess.” |
|
“Dwelling in” |
University: "So one of the coolest things is, which my students also discovered, that you can enter inside the model." Pre-school: "I mean, think about a child in a refrigerator box, that’s the best thing ever! So I think it has something to do with, it’s big, but it’s not too big. You know what I mean? It’s not child-size. It’s, 'Oh, my teacher can fit in it.' That makes it a little more unique." PD: “I did do some small-scale making with some magnets, stick and balls, but really there wasn’t that same interest level. I think the novelty of how big it was really was what drew them in so then we could start having those conversations around the project.” PD: “Not only I could fit inside of it, but I could fit other people. Yeah, we counted, ‘How many can we get inside?’” |
Discussion
Having presented, above, details of Ico’s design, implementation across diverse educational contexts, and reception by facilitators and participants in those contexts, we posit some implications and contextualize the above details as cases of more general characteristics that could be effectively implemented in other mathematics education activities.
Speaking back to theory
The nexus of movement, math, and constructionism
Ico speaks to the possibilities for constructionist mathematics education at body-scale. Consistent with nexus theory (Peppler & Wohlwend, 2018), each aspect of Ico truly lives at the intersection of three areas: body-scale movement, mathematics, and constructionism. It enables body-scale mathematical work that results in a public, shareable entity. This convergence produces practices, tools, and experiences unusual for math, from physical sensations of moving in space to social resources of collaboration to the emotional reactions to the finished result. More generally speaking, Ico simultaneously provides students with different possibilities of action-affordances both in meso- and micro-scale embodied spaces (Herbst et al., 2017). Thus, Ico is prototypical of situated geometry learning in a cross-scale embodied learning environment (Palatnik & Abrahamson, 2022).
Spotlighting often overlooked constructionist commitments
Reflections from interviewed educators support Ico’s alignment with constructionist pedagogical principles of continuity (using familiar materials), power (math serving the construction goal), and cultural resonance (a shareable product). More unusually, reactions to Ico underscore constructionism’s commitments to supporting diverse epistemologies. Constructing the Ico equally welcomes both bricoleur and top-down reasoning approaches (Turkle & Papert, 1991), with some participant groups choosing one or the other approach or even switching between them (“Some groups have followed the directions quite closely [...] Other groups just sort of started, like, let's try to build this."). Additionally, both the construction process and subsequent reasoning about the Ico’s geometric properties enable and even require a novel proximity as participants “dwell in” the shape, often constructing it around themselves and then stepping back to view the construction as a whole (Ackermann, 2001; Turkle & Papert, 1991). This dance between alternating proximity and distance (e.g., examining the in-progress shape as a whole, attending to particular incomplete vertices, stepping back to situate them) offers rich and unusual opportunities to attend to part-whole relationships of the shape, strengthening specific geometric knowledge and more general spatial reasoning.
True, Ico makes certain departures from constructionist tenets: the end-product is defined from the start, limiting opportunities for individual expression; and opportunities for long-term engagement are questionable, at least given the current materials. The dowels and tubing constituting Ico’s construction materials are a far-cry from the “protean machine,” as Papert (1980) dubbed computers. Yet, in a time when constructionism and even embodied learning are often assumed to be computer-based (Drijvers, 2019; Shvarts et al., 2021), Ico recalls the decidedly low-tech Brazilian samba schools that Papert (1980) celebrates as exemplar learning communities. Ico speaks to an often-implicit compromise of constructionism: activities need not embody all tenets of constructionism to be remarkably effective learning experiences.
Design
Material design facilitates interest and dissemination
The above design and interview analyses suggest that Ico’s appeal and spread across educational contexts was enabled by features of its material design, many of which strike a balance between seemingly oppositional pairs. The task is both serious — to construct a geometric object of conceptual complexity beyond most participant’s prior mathematical knowledge (“We had to actually practice saying the word.”) — and yet also playful (Papert & Harel, 1991), reminiscent of the construction kits familiar to many children (“I understand the basic shape and [...] how it can be connected. And so I started immediately to connect stuff”). For those who participate in Ico, the completed shape is transparent both in structure and process (Meira, 1998; Rabardel, 1995), yet making sense of its geometry is still a challenging and, at times, confusing task. The end-result is both expected — it is well-defined from the start of the task — and yet gratifying and satisfying (“[T]here are high fives. There's cheering. People are posting this on their social media.”). Perhaps most importantly, the Ico’s components are make-shift and accessible — assembled from off-the-shelf hardware-store materials and prepared in an hour or less (“30 minutes at Home Depot, and we were ready with 2 sets”) — yet the completed build is complex and feels of installation quality. In so many ways, this activity is more than the sum of its parts, prompting interest, enabling its spread, and inspiring other educational mathematics activities (e.g., Figure 2).
Implications for Educational Design
We next suggest two concrete lessons drawn from Ico and its spread that could inform the design of other educational experiences. First, we emphasize the ease of dissemination, when an engaging activity such as the Ico is readily accessible. The entire large Ico kit can cost less than $75, can be assembled in under an hour with no technical expertise, and its parts are both durable and easy to replace. Even in contrast to completely free digital resources, we suspect this blend of low cost and zero technical overhead was pivotal to Ico’s spread. Second, in creating this activity at the nexus of body-scale movement, mathematical activity, and constructionism, we closely consulted experts in each constituent area. Rather than trying to layer body-scale movement practices on top of mathematical activity, Ico instead highlights the mathematics of an existing artifact from dance and movement studies. This close collaboration and consultation with area experts is critical to ensure fidelity to domain-specific practices and, consequently, the convergence of practices so productive for engagement and learning.
Limitations
We acknowledge limitations within this research article, notably that it represents an after-the-fact design analysis rather than a premeditated effort to evaluate the efficacy of a set of identified design features. Further work is needed to understand the contributions and necessity of each identified feature for producing the documented results. Such work could inform and guide future efforts to design for productive convergence of domain practices in similarly captivating educational activities.
Conclusions
The Embodied Icosahedron activity (Ico for short), born as a lab inquiry into the history of choreographic notation, has now reached dozens of educators working with hundreds of learners aged 3 to 73. Ico interleaves design elements from three practices: body-scale movement, mathematics, and constructionist pedagogy. The apparent appeal of Ico—a low-tech activity—to diverse populations raises questions for a current zeitgeist of designing digital activities (Abrahamson et al., 2023; Penny, 2023). Ico reminds us that it is the quality of interaction, not the medium per se, that matters most. In its body-scale, Ico demonstrates the cognitive power and, therefore, pedagogical utility of literally “dwelling in” mathematics. Ico further suggests the value of low-cost concrete materials as an approachable entry point to unfamiliar concepts. Finally, Ico underscores the value of tasks at the intersection of mathematics and existing practices that already engender the engagement, curiosity, and wonder we hope for mathematics education to convey.
Acknowledgements
We are especially grateful to Christina Weihmann for (re)introducing us to the body-scale icosahedron, to Lisa Wymore for demonstrating to us its affordances for thinking about space and movement, and to Brenton Cheng for generously offering design guidance.
References
Abrahamson, D. (2009). Embodied design: Constructing means for constructing meaning. Educational Studies in Mathematics, 70(1), 27–47. https://doi.org/10.1007/s10649-008-9137-1
Abrahamson, D, & Rosenbaum, L. F. (2016, November 3). Embodied icosahedron activities [Participatory activity designed for the Embodied Mathematics, Imagination, and Cognition Working Group (EMIC)]. The 38th annual meeting of the North American chapter of the International Group for the Psychology of Mathematics Education, Tucson, AZ. https://edrl.berkeley.edu/wp-content/uploads/2021/10/Abrahamson.Rosenbaum.Embodied.Icosahedron.Activity.v7-Dor-ABRAHAMSON.pdf
Abrahamson, D., Ryokai, K., & Dimmel, J. K. (2023). Learning mathematics with digital resources: Reclaiming the cognitive role of physical movement. In B. Pepin, G. Gueudet, & J. Choppin (Eds.), Handbook of digital resources in mathematics education. Springer. https://doi.org/10.1007/978-3-030-95060-6_22-1
Abrahamson, D., & Trninic, D. (2015). Bringing forth mathematical concepts: signifying sensorimotor enactment in fields of promoted action. ZDM Mathematics Education, 47(2), 295–306. https://doi.org/10.1007/s11858-014-0620-0
Abrahamson, D., Trninic, D., Gutiérrez, J. F., Huth, J., & Lee, R. G. (2011). Hooks and shifts: A dialectical study of mediated discovery. Technology, Knowledge and Learning, 16(1), 55–85. https://doi.org/10.1007/s10758-011-9177-y
Ackermann, E. (1996). Perspective-taking and object construction. In Y. Kafai, & M. Resnick (Eds.), Constructionism in practice: Designing, thinking, and learning in a digital world (pp. 25 – 35). Lawrence Erlbaum Associates.
Ackermann, E. (2001). Piaget’s constructivism, Papert’s constructionism: What’s the difference? Future of Learning Group Publication, 5(3), 1 – 11. https://learning.media.mit.edu/content/publications/EA.Piaget%20_%20Papert.pdf
Adolph, K. E., Hoch, J. E., & Cole, W. G. (2018). Development (of walking): 15 suggestions. Trends in Cognitive Sciences, 22(8), 699–711. https://doi.org/10.1016/j.tics.2018.05.010
Alberto, R., Shvarts, A., Drijvers, P., & Bakker, A. (2022). Action-based embodied design for mathematics learning: A decade of variations on a theme. International Journal of Child-Computer Interaction, 32, Article 100419. https://doi.org/10.1016/j.ijcci.2021.100419
Alibali, M.W. & Nathan. M.J. (2012). Embodiment in Mathematics Teaching and Learning: Evidence from learners' and teachers' gestures. Journal of the Learning Sciences, 21:2, 247-286, https://doi.org/10.1080/10508406.2011.611446
Allen, J. W. P., & Bickhard, M. H. (2013). Stepping off the pendulum: Why only an action-based approach can transcend the nativist–empiricist debate. Cognitive Development, 28(2), 96–133. https://doi.org/10.1016/j.cogdev.2013.01.002
Araujo, D., & Davids, K. (2004). Embodied cognition and emergent decision-making in dynamical movement systems. Junctures: The Journal for Thematic Dialogue, 2, 45-57. https://junctures.org/index.php/junctures/article/view/150
Arzarello, F., Paola, D., Robutti, O., & Sabena, C. (2009). Gestures as semiotic resources in the mathematics classroom. Educational Studies in Mathematics, 70(2), 97–109. https://doi.org/10.1007/s10649-008-9163-z
Arzarello, F., & Robutti, O. (2004). Approaching functions through motion experiments. Educational Studies in Mathematics, 57(3), 305-308. https://www.jstor.org/stable/4150294
Arzarello, F., Robutti, O., & Bazzini, L. (2005). Acting is learning: Focus on the construction of mathematical concepts. Cambridge Journal of Education, 35(1), 55–67. https://doi.org/10.1080/0305764042000332498
Benally, J., Palatnik, A., Ryokai, K., & Abrahamson, D. (2022). Learning through negotiating conceptually generative perspectival complementarities: The case of geometry. For the Learning of Mathematics, 42(3), 34–41. https://escholarship.org/uc/item/62z5t879
Blikstein, P., Martinez, S. L., Pang, H. A., & Jarrett, K. (2016). Meaningful Making: Projects and inspirations for fab labs + makerspaces. Constructing Modern Knowledge Press.
Cadoret, G., Bigras, N., Duval, S., Lemay, L., Tremblay, T., & Lemire, J. (2018). The mediating role of cognitive ability on the relationship between motor proficiency and early academic achievement in children. Human Movement Science, 57, 149–157. https://doi.org/10.1016/j.humov.2017.12.002
Cavallo, D. (2000). Emergent design and learning environments: Building on indigenous knowledge. IBM Systems Journal, 39(3), 768–781. https://ieeexplore.ieee.org/abstract/document/5387027
Chong, C.-H., & Yeo, K.-J. (2015). An overview of grounded theory design in educational research. Asian Social Science, 11(12), 258-268. https://doi.org/10.5539/ass.v11n12p258
Dinehart, L., & Manfra, L. (2013). Associations between low-income children’s fine motor skills in preschool and academic performance in second grade. Early Education & Development, 24(2), 138–161. https://doi.org/10.1080/10409289.2011.636729
Drijvers, P. (2019). Embodied instrumentation: Combining different views on using digital technology in mathematics education. In U. T. Jankvist, M. van den Heuvel-Panhuizen, & M. Veldhuis (Eds.), Eleventh Congress of the European Society for Research in Mathematics Education (pp. 8-28). Utrecht University and ERME. https://hal.science/hal-02436279
Duijzer, A. C. G., Shayan, S., Bakker, A., van der Schaaf, M. F., & Abrahamson, D. (2017). Touchscreen tablets: Coordinating action and perception for mathematical cognition. Frontiers in Psychology, 8(144). https://doi.org/10.3389/fpsyg.2017.00144
Durán–López, E., Iyer, G. V., & Rosenbaum, L. F. (2017). Geometris: A collaborative embodied geometry game. In G. Mark, S. Fussel, F. Mueller, & J. Tanenbaum (Eds.), Proceedings of the 2017 CHI Conference Extended Abstracts on Human Factors in Computing Systems (pp. 214-217). CHI. https://doi.org/10.1145/3027063.3048413
Fedewa, A. L., & Ahn, S. (2011). The effects of physical activity and physical fitness on children’s achievement and cognitive outcomes: A meta-analysis. Research Quarterly for Exercise and Sport, 82(3), 521–535. https://doi.org/10.1080/02701367.2011.10599785
Feldenkrais, M. (1981). The elusive obvious. Meta Publications.
Fischer, U., Suggate, S. P., Schmirl, J., & Stoeger, H. (2018). Counting on fine motor skills: links between preschool finger dexterity and numerical skills. Developmental Science, 21(4), e12623. https://doi.org/10.1111/desc.12623
Gerofsky, S. (2010). Mathematical learning and gesture: Character viewpoint and observer viewpoint in students’ gestured graphs of functions. Gesture, 10(2–3), 321–343. https://doi.org/10.1075/gest.10.2-3.10ger
Gerofsky, S. (2011). Seeing the graph vs. being the graph: Gesture, engagement and awareness in school mathematics. In G. Stam & M. Ishino (Eds.), Integrating gestures (pp. 245–256). John Benjamins.
GrandpaSafari. (2008, May 24). Forsythe-Lines-Point point line-2-Extrusion [Video choreographed and performed by William Forsythe]. YouTube. https://www.youtube.com/watch?v=e_7ixi32lCo
Grissmer, D., Grimm, K. J., Aiyer, S. M., Murrah, W. M., & Steele, J. S. (2010). Fine motor skills and early comprehension of the world: Two new school readiness indicators. Developmental Psychology, 46(5), 1008-1017. https://psycnet.apa.org/doi/10.1037/a0020104
Hall, R., Ma, J. Y., & Nemirovsky, R. (2015). Rescaling bodies in/as representational instruments in GPS drawing. In V. R. Lee (Ed.), Learning technologies and the body: Integration and implementation in formal and informal learning environments (pp.112–131). Routledge.
Herbst, P., Boileau, N., Clark, L., Milewski, A., Chieu, V. M., Gürsel, U., & Chazan, D. (2017). Directing focus and enabling inquiry with representations of practice: Written cases, storyboards, and teacher education. In Galindo, E., & Newton, J., (Eds.). Proceedings of the 39th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 789-796). Hoosier Association of Mathematics Teacher Educators.
Hutto, D. D., Kirchhoff, M. D., & Abrahamson, D. (2015). The enactive roots of STEM: Rethinking educational design in mathematics. Educational Psychology Review, 27(3), 371–389. https://doi.org/10.1007/s10648-015-9326-2
Kegan, R. (1982). The evolving self: Problem and process in human development. Harvard University Press.
Kelton, M. L., & Ma, J. Y. (2020). Assembling a torus: Family mobilities in an immersive mathematics exhibition. Cognition and Instruction, 38(3), 318–347. https://doi.org/10.1080/07370008.2020.1725013
Knoll, E., Landry, W., Taylor, T., Carreiro, P., & Gerofsky, S. (2015). The aesthetics of scale: Weaving mathematical understandings. In K. Delp, C. S. Kaplan, D. McKenna, & R. Sarhangi (Eds.), Proceedings of Bridges 2015: Mathematics, Music, Art, Architecture, Culture (pp. 533–540). Tessellations Publishing.
Luo, Z., Jose, P. E., Huntsinger, C. S., & Pigott, T. D. (2007). Fine motor skills and mathematics achievement in East Asian American and European American kindergartners and first graders. British Journal of Developmental Psychology, 25(4), 595–614. https://psycnet.apa.org/doi/10.1348/026151007X185329
Ma, J. Y. (2017). Multi-party, whole-body interactions in mathematical activity. Cognition and Instruction, 35(2), 141–164. https://doi.org/10.1080/07370008.2017.1282485
Malinverni, L., & Pares, N. (2014). Learning of abstract concepts through full-body interaction: A systematic review. Journal of Educational Technology & Society, 17(4), 100–116. https://www.jstor.org/stable/jeductechsoci.17.4.100
Meira, L. (1998). Making sense of instructional devices: The emergence of transparency in mathematical activity. Journal for Research in Mathematics Education, 29(2), 121–142. https://doi.org/10.2307/749895
Mickelson, J., Canton, M., & Ju, W. (2011). Pattern poses: Embodied geometry with tangibles and computer visualization. In T. Moher & C. Quintana (Eds.), Proceedings of the 10th International Conference on Interaction Design and Children (pp. 242–245). ACM. https://doi.org/10.1145/1999030.1999072
National Council of Teachers of Mathematics (NCTM). (2000). Principles and standards for school mathematics.
National Governors Association Center for Best Practices & Council of Chief State School Officers. (2010). Common core state standards.
Nemirovsky, R., Kelton, M. L., & Rhodehamel, B. (2013). Playing mathematical instruments: Emerging perceptuomotor integration with an interactive mathematics exhibit. Journal for Research in Mathematics Education, 44(2), 372–415. https://doi.org/10.5951/jresematheduc.44.2.0372
Nemirovsky, R., Tierney, C., & Wright, T. (1998). Body motion and graphing. Cognition and Instruction, 16(2), 119–172. https://www.jstor.org/stable/3233719
Orth, D., van der Kamp, J., Memmert, D., & Savelsbergh, G. J. P. (2017). Creative motor actions as emerging from movement variability. Frontiers in Psychology, 8. https://doi.org/10.3389/fpsyg.2017.01903
Palatnik, A. (2022). Students’ exploration of tangible geometric models: Focus on shifts of attention. In C. Fernández, S. Llinares, A. Gutiérrez, & N. Planas (Eds.). Proceedings of the 45th Conference of the International Group for the Psychology of Mathematics Education (Vol. 3, pp. 275–282). PME.
Palatnik, A. & Abrahamson, D. (2022). Escape from Plato’s cave: An enactivist argument for learning 3D geometry by constructing tangible models. In G. Bolondi, F. Ferretti, & C. Spagnolo (Eds.), Proceedings of the Twelfth Congress of the European Society for Research in Mathematics Education (CERME12) (pp. 742 – 749). Free University of Bolzano and ERME.
Papert, S. (1980). Mindstorms: Children, computers, and powerful ideas. Basic Books.
Papert, S., & Harel, I. (1991). Situating constructionism. In I. Harel & S. Papert (Eds.), Constructionism: Research reports and essays (pp. 1-11). Ablex Publishing.
Penny S. (2023) Living in mapworld: Academia symbolic abstraction and the shift to online everything. Constructivist Foundations, 18(2), 188-198. https://constructivist.info/18/2/188
Peppler, K., & Wohlwend, K. (2018). Theorizing the nexus of STEAM practice. Arts Education Policy Review, 119(2), 88–99. https://doi.org/10.1080/10632913.2017.1316331
Piaget, J. (1971). Biology and knowledge: An essay on the relations between organic regulations and cognitive processes. University of Chicago Press.
Rabardel, P. (1995). Les hommes et les technologies; approche cognitive des instruments contemporains. Armand Colin. https://hal.science/hal-01017462
Reed, E. S., & Bril, B. (1996). The primacy of action in development. In M. L. Latash & M. T. Turvey (Eds.), Dexterity and its development (pp. 431-451). Lawrence Erlbaum Associates.
Rosenbaum, L. F., Kaur, J., & Abrahamson, D. (2020). Shaping perception: Designing for participatory facilitation of collaborative geometry. Digital Experiences in Mathematics Education, 6(2), 191–212. https://doi.org/10.1007/s40751-020-00068-2
Rosenfeld, M. (2017). Math on the move: Engaging students in whole body learning. Heinemann.
Sheets-Johnstone, M. (2011). The Primacy of Movement (2nd ed.). John Benjamins Publishing. https://doi.org/10.1075/aicr.82
Shoval, E. (2011). Using mindful movement in cooperative learning while learning about angles. Instructional Science, 39(4), 453–466. https://doi.org/10.1007/s11251-010-9137-2
Shvarts, A., Alberto, R., Bakker, A., Doorman, M., & Drijvers, P. (2021). Embodied instrumentation in learning mathematics as the genesis of a body-artifact functional system. Educational Studies in Mathematics, 107(3), 447–469. https://doi.org/10.1007/s10649-021-10053-0
Tancredi, S., Abdu, R., Balasubramaniam, R., & Abrahamson, D. (2022). Intermodality in multimodal learning analytics for cognitive theory development: A case from embodied design for mathematics learning. In M. Giannakos, D. Spikol, D. Di Mitri, K. Sharma, X. Ochoa, & R. Hammad (Eds.), The multimodal learning analytics handbook (pp. 133-158). Springer International Publishing. https://doi.org/10.1007/978-3-031-08076-0_6
Turkle, S., & Papert, S. (1991). Epistemological pluralism and the revaluation of the concrete. In I. Harel & S. Papert (Eds.), Constructionism: Research reports and essays (pp. 161–192). Ablex Publishing.
Varela, F. J., Thompson, E., & Rosch, E. (2017). The embodied mind, revised edition: Cognitive science and human experience. MIT Press.
Vogelstein, L., Brady, C., & Hall, R. (2019). Reenacting mathematical concepts found in large-scale dance performance can provide both material and method for ensemble learning. ZDM Mathematics Education, 51(2), 331–346. https://doi.org/10.1007/s11858-019-01030-2
Walkington, C., Chelule, G., Woods, D., & Nathan, M. J. (2019). Collaborative gesture as a case of extended mathematical cognition. The Journal of Mathematical Behavior, 55. Article 100683. https://doi.org/10.1016/j.jmathb.2018.12.002
Wilson, M. (2002). Six views of embodied cognition. Psychonomic Bulletin & Review, 9(4), 625–636. https://doi.org/10.3758/BF03196322
Footnotes
-
In May of 2016, Dor received an email from Christina Weihmann, a Hamburg-based special-education scholar and practitioner who uses movement as the foundation of her therapy. Christina re-introduced Dor to Laban’s work promoting movement within an icosahedron and suggested that Lisa Wymore, Professor of Theater, Dance, and Performance Studies at UC Berkeley, could be a good local resource. Dor invited Lisa to visit his research group to discuss and possibly demonstrate Laban’s use of the icosahedron. To prepare for Lisa’s visit to his lab, Dor received direction from Brenton Cheng, Lisa’s associate, on how to construct the large-scale icosahedron from supplies found at a local hardware store. Based on the level of interest during Lisa’s visit, Dor and Leah built out the full activity guide.
-
These names are pseudonyms.



