Hands-on Mathematics Activities in Malawian Primary Schools
Abstract
Because of large class sizes and very few resources for schools, most classrooms in Malawi are dominated by teacher talk and pupils find learning mathematics hard. This article describes the outcomes of the author’s research and practical experiences in Malawi developing hands-on mathematics activities to increase conceptual understanding, problem solving, skills and engagement in this difficult context. After initial research in Malawian classrooms, the author achieved considerable success over five years in teacher in-service courses where teachers had first-hand experience of working together in small groups with hands-on materials. Simple, inexpensive, and effective hands-on materials made from paper and using playing cards are described. There is an impressive report of a teacher taking these methods back to her school. Small groups helped students learn from and support each other, often using the local language before formal English words are introduced. Even in large classes such as those in Malawi, carefully designed hands-on teaching activities using small group work are manageable.
The challenge of improving mathematics teaching in Malawi

Click to enlarge

Click to enlarge
In Malawian primary schools, class sizes can average 100, teachers are poorly trained, textbooks are poor and rare, and classrooms are dominated by teacher talk. Consequently, results are very poor. Finding a way to improve this situation was a challenge I accepted after meeting a Malawian educator. I embarked on a PhD thesis involving researching in primary schools in southern Malawi in 2008, gathering data on how mathematics was being taught. This led to visits to Malawi in the years up to 2015 conducting in-service courses for up to 60 teachers at a time, using hands-on teaching methods, previously regarded by Malawian teachers as impossible in large classes, which I subsequently incorporated into textbooks prepared for publication in Malawi. This article explains the choice of hands-on activities used in these courses. I have demonstrated that hands-on methods work in large (Malawian) classes, to increase conceptual understanding, develop and practise skills, and challenge thinking skills through puzzles and problem solving.
From Melbourne to Malawi
I live in Melbourne, Australia. In 2000 I met Willy Mwakapenda (see Figure 1), a Malawian studying for PhD at a university in Melbourne, Australia. Subsequently, I visited Malawi in 2005 for PhD research (Lowe, 2008), and from 2009 to 2014 to run a series of in-service courses for many hundreds of teachers, mainly from primary schools. During my 6.5 weeks in the country, I was fortunate to live in Domasi with Grames Chirwa (see Figure 2), a staff member of the Institute of Education, who also acted as a guide. My thesis was largely about primary education in the very crowded schools, but since I had previously had a long career as an innovative mathematics teacher and author in Australia, Canada and Samoa, I chose to focus on how mathematics education was being conducted in 2008.



Click to enlarge
Croft (2002) described how a typical teacher in southern Malawi conducts her classes, ‘singing under a tree’. I observed an example of this where a teacher of Standard 1 (first year of school) had using chant-response singing. A photo of part of such a class is shown in Figure 3. The average class size in the 10 schools I visited was 100, with the largest being 403 (in a Standard 1 class). This, plus the severe lack of proper training and equipment for teaching under these conditions, has led to the educational outcomes that are described below. The appendix contains more information about Malawi, its history, culture, social conditions, and education.

I returned to Malawi to share the results of my thesis, and for in-service courses for a few weeks each year between 2008 to 2014. The locations were in the four major centres: Zomba, Lilongwe, Mzuzu, and Blantyre. From my personal perspective this was an expensive program as it was almost totally unsupported. This was partly due to the Malawian expectation of being paid to attend courses. Organization of these week-long courses required the cooperation with the Association of Christian Educators of Malawi and various church education authorities.
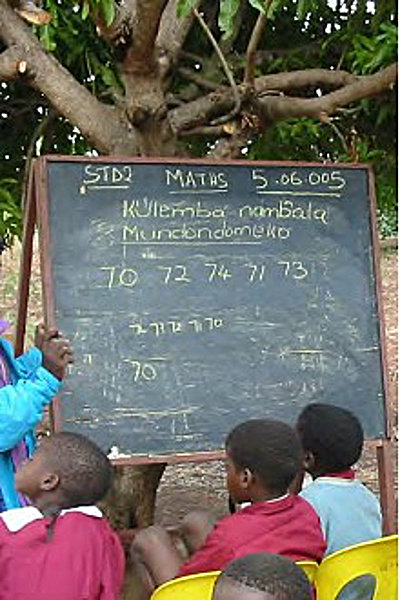
Click to enlarge
Performance in mathematics: teachers and pupils
Teachers have successfully struggled through two years of secondary education, frequently in private fee-paying schools, and then had little preparation for teaching in a primary classroom. There is little support even for rote learning in the mathematics text books, and no support to help pupils (or teachers) understand any mathematics concepts. My research suggests that, in 2005, many Malawian primary teachers had very little understanding of basic concepts of mathematics, or even that such ideas exist. To get some notion of the mathematics performance of Malawian primary pupils, we may refer to comparative results (Sandefur, 2016). He has used statistical methods to compare results in TIMMS with roughly equivalent sub-Saharan national test results known as SACMEQ. In his ranking using the TIMMS grade 4 scale, the Malawian performance is second from the bottom of 61 listed countries, just above Namibia.
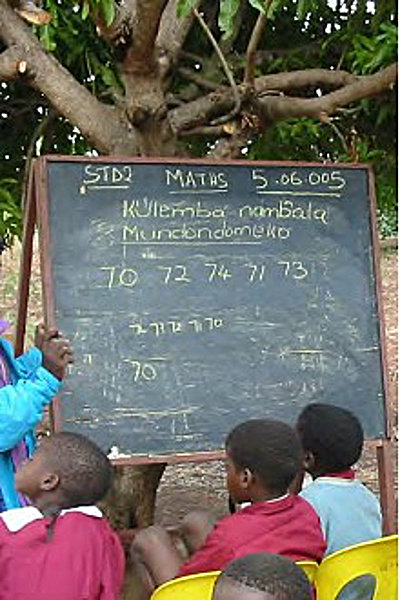
I compare three different equating methods and find that learning levels in this sample of African countries are consistently (a) low in absolute terms, with average pupils scoring below the fifth percentile for most developed economies; (b) significantly lower than predicted by African per capita GDP levels; and (c) converging slowly, if at all, to the rest of the world during the 2000s. (Sandefur, 2016, p1)
In my classroom research in Malawian primary schools, I observed much teaching by repetition. There was no attempt at developing understanding, and many teachers appeared to have no idea that mathematics could be understood. Teachers generally had memorised rules (e.g., about moving the decimal point) but struggled to explain why these rules work. For example, they needed a lot of time to see that 30 × 0.4 is the same as 3 × 4, as well as to understand why. In my research I had discovered teachers who had no ideas about the ways decimals were used in real life. They knew about money and measurement but had never linked these applications to decimal numbers.
The textbooks for Standards 1 to 4 are in Chichewa, but those for Standards 5 to 8 are written in English, leading many pupils to drop-out (or repeat a year) when they cannot cope with the added challenge of language. Their textbooks give worked examples for exercises but no explanations. In the classrooms I visited, textbooks were rare.
What can be done to improve this situation in Malawi?
Accepting the challenge
In my teaching career I have had the privilege of first reading books about hands-on methods of teaching mathematical ideas by Zoltan Dienes, and later meeting and observing Dr Dienes teaching in Quebec. I have successfully used these methods (though not with the same content) to teach school students, youth and adult groups in Australia, and once I became a consultant, I found that these methods are very successful with teachers and in pre-service courses. The essence of Dienes’ methods is discussion of mathematical ideas within groups, based on the extensive use of hands-on materials (Dienes, 1971).
After a lifetime of innovative teaching, I am firmly convinced that, without conceptual understanding, mathematical skills are meaningless and cannot be applied in any novel situation. This emphasis on conceptual understanding does not preclude skill development and problem solving; they remain important parts of the total package. For many students (and some teachers of mathematics) worldwide, a lack of understanding, motivation and success in mathematics classes (and tests) leads to a lack of confidence when using mathematics, and so these students avoid the use of mathematics in daily life whenever possible.
Teaching methods must be used that engage and motivate pupils to understand and enjoy the experience of learning mathematics. My way to improve engagement is through the use of group work, where pupils can speak to one another instead of listening to the teacher (and turning off). Group work is also possible in large classes.
Later I discovered that the American Institute for Research project IEQ/Malawi (2003) had tried new teaching methods in lower primary levels. They set up learning tools and assessments and trained teachers in group work methods, as discussed in Lowe (2008). They found that this worked successfully in the large classes where they tried it. Unfortunately, there was little or no take up from teachers or the Ministry of Education.
This gave me the confidence to try a teaching method that I had been using very successfully for most of my teaching career in Australian secondary schools and teachers’ colleges: successful group work, using hands-on materials. Therefore, I accepted the challenge of introducing these new methods of teaching and learning into Malawi. I did this through a series of visits to Malawi over several years, including with the workshops for teachers that are outlined below.
Improving engagement though group work with hands-on materials
During my time in Malawi, I was able to use small group work very successfully with large groups of teachers (over 60 at a time in a workshop) with a clear focus on group learning activities. The message that was readily accepted by the hundreds of teachers present at these sessions was that pupils’ engagement needs hands-on activities; in the words of teachers ‘hands-on, minds-on’.
I chose activities that would be of direct use if teachers later imitated me in their own classrooms. After involving groups of teachers in hands-on activities, with feedback to the entire workshop group, I also discussed the pedagogy involved, pointing out how I was able to get them all involved. In that way I was hoping that they would develop confidence to use the same methods, but with some understanding of what factors were important.
About the workshops
Some workshops were one or two days, while some lasted one entire week, while I paid for the accommodation. Each day included a range of activities: mathematical card games, hands-on concept learning activities and problem solving. Sessions between breaks lasted 60 to 90 minutes, and each session ended with pedagogical discussion. Although many teachers spoke in Chichewa (the local language) during group activities, at the end of each group activity, they reported their learnings and I summarised in English.
The teacher’s role in a hands-on classroom
In a hands-on classroom, the teacher’s role is to increase the involvement of the pupils in the mathematical activities. I pointed out to the teachers that this is done in several ways.
-
Organising small groups of pupils around the tasks, providing hands-on materials as needed and making sure that they understand the problem they are trying to solve.
-
Assisting the groups to work together on the group activity, including providing a time deadline.
-
Selecting someone to report to the class about the findings of their group.
-
Summarising the findings of different groups and relating the new knowledge to previous activities and knowledge.
One of the advantages of pupils working in small groups is the fact that they can, and do, explain ideas to each other in Chichewa (or another ‘home’ language shared by group members).
In large classes teaching aids must be inexpensive and, in many cases, should be shared by the members of each small group. In these workshops I used playing cards (imported from Australia but readily available in all Malawian homes), and plain copy paper (purchased in Malawi).
Hands-on activities develop mathematical concepts, problem solving and skills
I found that most Malawian primary teachers lacked any idea about place value, and with this hands-on approach they were able to understand how it applies to all four arithmetical operations with whole numbers. Paper models of base 10 are inexpensive – using only two sheets of A4 paper, as long as we stay with 1s, 10s and 100s. Later, we renamed the large square as 1, so we had a model for decimals (to hundredths) and also for percentages.
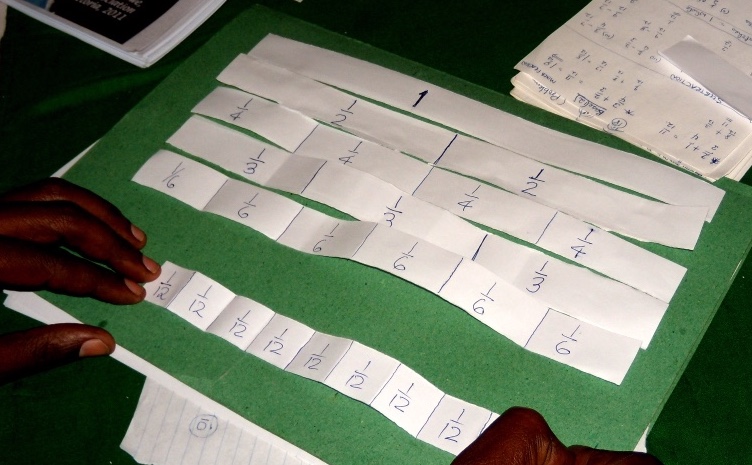
A simple paper model of fractions requires only one sheet of A4 paper. For most teachers it was a revelation to be understanding the ideas of equivalent fractions for the first time, and moving to understand why the four operations work as they do. The next section gives details of the model.
All Malawian homes have packs of playing cards. Teachers have reported that they have no problem getting pupils to bring a pack to school. Alternatively, each pupil can cut one sheet of A4 paper into 40 rectangles and make a set of ‘cards’ (1 to 10 in four colours). These may be used for problem solving if each pupil has their own set.
In my in-service courses, the most popular activities were the card games, to be played in small groups (four to six). We needed one set of cards per group. Sometimes tens and court cards became zeros, but sometimes the values 10 to 13. Aces were always 1. The card games are generally self-correcting and allow peer teaching.

Enlarge…
Understanding fractions using hands-on learning
I started each session about fractions by helping each teacher to make their own fraction strips, by folding and cutting one sheet of A4 paper. This activity gets the teachers (and their pupils) personally involved with the fractions as everyone had their own set. The fraction model is based on strips of equal length cut from one sheet of A4 paper. It includes all fractions with a factor of 12 as denominator. Figure 5 shows a complete set of fraction strips, made by folding. Teachers used the strips to explain the operations and relate the lengths on the paper strips to the procedures that teachers knew, but had never understood. After making their strips, pupils use them to explore the meaning of fractions as numbers and the operations on them, including:
- Equivalent fractions (e.g., a half -strip and two quarter-strips are the same length).
- Mixed numbers and improper fractions. Equivalence of a mixed number and an improper fraction can be seen from comparing the associated strips. E.g., a one-strip and 2 third-strips () compared to 5 third-strips ().
- Addition. Strips are folded and the lengths added, (e.g. ). The task is then to find the strip (or combination of strips that allows us to name this total (e.g., ), and show how it relates to the algorithm. Similar methods apply for subtraction.
- Multiplication. Using the English word ‘of’, we find etc.
- Division. Use the divisor as a ‘measurer’ to see how many times the divisor fits into the dividend e.g., the one-half strip fits into the three quarters strip one and a half times:
Developing problem solving
Mathematical problem solving is unknown in Malawian primary classrooms. However, I have demonstrated that well-chosen activities are both very motivating and successful in developing problem solving skills and hence boost self-confidence, both for teachers and students. This section provides three examples.

Enlarge…

Enlarge…
Crosses
Crosses (see Figure 6) is a rich activity involving problem solving at many levels: trial and error, searching for patterns, finding one and then more solutions, and proving that you have found all the solutions. Using numbers 1 to 9 the challenge is to arrange the cards so that the sum vertically is the same as the sum horizontally. After finding one solution, you are challenged to find them all and then prove that there are no more.
Triangle 1-6 puzzle
This challenge allowed me to introduce the elements of problem solving. Only cards 1 to 6 are needed to complete this task. Use all cards (one for each vertex, one for each side) so that the total of each three-card edge adds to the same number. After finding one solution, find them all, and explain why there are no more. Teachers working on this problem are shown in Figure 7. All teachers soon find one solution (usually by trial and error) and are then challenged to find all solutions. They often choose a more systematic search. Finally, they are challenged to prove that there are no more solutions.



Enlarge…
Kangaroos
The Kangaroos activity shown in Figure 8 involves counting the number of moves (jumps and slides) needed to complete the swapping of sides with different numbers of ‘kangaroos’ on each side. You may know this as the jumping frog puzzle. It begins with a straightforward initial puzzle but can be taken much further. We used both sides of bottle-tops, or bottle-tops of different colours.
Initial puzzle: Three kangaroos meet three other kangaroos meet going in opposite directions along a mountain path. There is a space large enough for one kangaroo between them. Without leaving the path, how can the two groups swap places? How many jumps and hops does it take? These kangaroos can jump over one other kangaroo at a time. They cannot go backwards to make more space and they can only jump when adjacent.
Quadratic function version: By changing the number of kangaroos on each side, the puzzle is extended. How many moves are needed to swap places? Using the variables y (for the number of moves) and x (for the number of kangaroos on each side) find a formula for the function relating x to y. There are three different, but equivalent, formulas; find them all. The insight can even be extended to having different numbers of kangaroos on each side.

Teaching methods used in the workshops
As the use of hands-on materials was new to these teachers, I modelled how they could introduce these methods to their own classes when introducing hands-on methods to them. This involves some careful demonstration, often with teachers standing around watching, and then setting tasks for them to perform in small groups with their own sets of materials.
Groups of four to six learners were formed, so that there were opportunities for peer teaching in their own language as they engaged in a clearly defined activity with a stated deadline. Each group had one set of simple equipment to share. There was a lot of chatter, but it was rarely unproductive. Through this use of group work, learners (teachers or pupils) can help each other – in the home or national language they can understand.
At the end of each group activity, there was some reporting of their learnings – in English. Then I summarised the ideas using correct mathematical language in English, and they all understood; they had been engaged in forming the ideas for themselves and learned how they are labelled in English.

Enlarge…
The experience of Calister Phiri
Of the 75 teachers I taught on a week-long course in 2011 (in the Malawian capital Lilongwe), only two used email, and so were able to keep in contact with me in future years. One of these two, Calister Phiri, had extremely good results in future Standard 8 examinations over many years, which she attributed to using hands-on teaching methods in mathematics. Figure 9 shows us together. This teacher had attended my week-long workshop in 2011 and she helped me with the workshops in 2012, 2013 and 2014. She ran her own workshops in local Mzuzu schools over several years, and she was awarded ‘outstanding teacher’ for her work, particularly in mathematics. In 2021 she was appointed head teacher in a local primary school. She has recently become a consultant, to further enable her to assist others with hands-on methods. She has given me permission to tell her story in her own words and share her photo. Below are extracts from email correspondence to me over several years. Calister progressed from a classroom teacher to head teacher and educational consultant, largely based on her amazing results, which were largely due to her use of hands-on teaching methods.

Message in 2013: “At my school we used to have poor results more especially in Maths, but an improvement started when I learned some skills and knowledge of imparting in learners and my fellow teachers. In 2010 at my school we had 120 learners who sat for secondary exams and only 74 were selected to various secondary schools, out of these only 20 of these got good grades in maths. In 2011 we had 127 learners and 92 of them got selected to go to secondary schools, 62 of them passed with good grades in maths. In 2012 we had 125 learners in Std 8 and 100 learners were selected to secondary schools and the school was awarded position 1 at District level. In 2013 we maintained the lead in maths and the entire passing rate in the District with 93% pass rate.”
Message in 2014: "The MANEB results are out and the passing rate for maths has increased from 83% to 96% at my school. I can't believe it honestly. Again, not any other school in our zone has such results. Am now at my new school busy with my hands-on activities. The learners are very happy with my teaching. They have even confessed that they are understanding maths better now than ever.”
Message in 2016: “As for my last year' s results, it was wonderful as usual. though with few grade As but many Bs and few Cs. I was still on top in my zone. This is all because of you, Ian, teaching me the Hands-on methods. It really works.”
In summary

Enlarge…
Malawi provides an example of inequality of background and opportunity on a national level; it is a good example of the disparity of development on a global scale. (See Figure 10 for an illustration). Natural justice requires that opportunities are taken to assist teachers in such countries use education to move development forward.
When choosing teaching methods to model to teachers in a country like Malawi, account should be taken of the culture and educational background of the teachers. They should also be methods that could be used by those teachers back in their own classrooms. The resources required to be successful in newly introduced teaching methods must be within the capacity of schools to afford and to organise. The paper models for mathematical concepts are inexpensive, and the cards used for puzzles and games are available in homes or easily made from paper.

The methods should also allow teachers lacking conceptual understanding or skills to improve these while joining in with pupils in their activities. Above all, the methods should engage pupils (and teachers) positively in the experience of learning.
I have shown that it is possible to use hands-on teaching methods to increase opportunities for engagement through group work, that this is manageable in a large class, and that it allows pupils to support each other in their home or national language. I focused on the three major components of mathematics learning: understanding of mathematical concepts, fluency with mathematical skills and problem solving.
Appendix: About Malawi
A brief description of Malawi
In order to establish the urgent need for justice based on extraordinary levels of inequality, this section briefly describes Malawi: its history, economy, health, and some aspects of its way of life. Malawi is one of the poorest countries in the world. The population is 80% rural, so its economy is largely subsistence, and most homes are without power. The culture includes few books, and is mainly oral, depending on radio for news and entertainment. Despite this, most adults will have a simple battery-operated cell phone.
All the sub-Saharan countries have poorly performing education systems, with overcrowded schools and very large classes, especially in lower primary levels. Malawi is near the bottom of this group of countries. As a consequence, rote learning is rife, and teacher talk dominates all lessons.
The world includes many countries like Malawi, where circumstances have conspired to leave the majority of the population behind in economic development and quality of life. Among the wealthy nations, there is a tendency to focus on our own needs, inequalities and to stay ahead of similarly wealthy nations. I had previously worked in educational projects in Western Samoa, and so I was drawn to use that previous experience and background in mathematics education, to assist Malawi on the premise that economic development requires a population competent in mathematics in order to develop new industries and to improve the efficiency of those that presently exist.
Malawi suffered severely during the years of the slave trade. David Livingstone was mainly responsible for ending this tragedy. Malawi became a British Protectorate named Nyasaland – literally ‘land of the lake’ – and the large lake along its eastern border was once called Lake Nyasa.
Although being administered from London, much of the civic structure was created by Scottish missionaries. This included the education system, which was in two fairly distinct streams; an academic stream led to English certifications, and a more practical one to help improve farming methods. These two emphases have been in conflict ever since.
Malawi has a rapidly growing population (annually 2.7%) similar to much of sub-Saharan Africa. Within its small area it has the highest population density for any African nation. Only 20% live in the four major towns: Lilongwe (capital), Blantyre (largest), Mzuzu, and Zomba.
Malawi has very few natural resources. Its largest industry, established during the British management, is tobacco, for which the market remains in rapid decline. There are no minerals. Due to deforestation, there are far fewer trees than there could be, and a growing timber industry, largely for local construction, is reducing the few forests that remain.

Enlarge…
Malawians live largely in villages with large families in mud brick houses, as shown in Figure 11. Most families are dependent on subsistence: they work in plantations or other outdoor farming or fishing (Government of Malawi, 2002). Children are expected to make their own contributions, particularly at the time of the maize harvest. School vacations are organised around this economic requirement. Information and entertainment come through radio and simple cell phones. Large families frequently gather for card games and other social events.
Nothing about Malawi’s history should avoid mentioning the HIV-AIDS epidemic. Malawi was second only to South Africa in the prevalence of the HIV-AIDS epidemic. The large numbers of children without one or both parents as a result of this disease causes stress, and distress, in the education system as well as the community as a whole.

The Malawian education system
The academic vs practical tension
In the early years, missionary schools conducted classes in English, preparing a few boys for English universities. Girls, and many boys who could not make the academic grade, were trained in home economics (girls) or farming (boys), conducted in the pupils’ home language.
Malawi was granted independence in 1964. A newly elected democratic government abolished school fees. As a result of this, school education (previously requiring fees) became ‘free’, so school populations almost doubled. However, the numbers of classrooms and staff remained the same, and this dramatic caused a dramatic lowering of quality of outcomes, that is still in progress.
Languages
As Malawi comprises several tribes, there are many home languages. In southern Malawian schools most pupils speak their tribal language at home, the ‘national language’ (Chichewa) at school up to Standard 4, and then English (required after Standard 4). This area of education is hotly contested, but the leaving certificate (at the end of Standard 8) is entirely in English, except for the subject ‘Chichewa’.
Curriculum and Assessment
The primary curriculum was revised in 2004. The revision was called “Primary Curriculum and Assessment Reform” (PCAR). In the subject of mathematics, it leant strongly towards the ‘academic’ preparation for the examination, rather than anything practical for use in daily life, despite clearly stating practical goals at the start of the syllabus.
I obtained an electronic copy of the PCAR mathematics courses from Standards 1 to 8. My detailed study of the new mathematics courses shows that PCAR has gone the way of the 1991 course, preparing pupils for examinations and almost ignoring the stated goal. The detailed syllabus reflects an abstract number-oriented progression through clear stages, readily interpreted as preparation for the examinations. There is virtually no mention of ‘daily life’ applications. (Lowe, 2008)
The leaving certificate examination (ending Standard 8) is used to select those few who get ‘free’ secondary education and so good performance is the chief goal of primary education. As a result, yearly assessments in all subjects (seen as preparation for the big one at the end) dominate the progress throughout primary school. Because the spread of percentage marks in mathematics is usually far wider than the spread in other subjects, mathematical outcomes also dominate the final ‘average’ mark used to determine success or failure.
There is no practice of ‘automatic progression’ in Malawi. Those who ‘fail’ the tests at the end of each year may either repeat or drop out of school. The rates of repetition in 2005 varied from 10% (Standard 7) to 25% (Standard 1). The rates of drop-out in 2005 were very similar. Due to the cumulative effect of repeating years, there is a very large age-range in classes. In 2005 Standard 1 included ages 4 to 12, and Standard 8 ages 11 to 18. In their repeating year, those who are repeating still perform at a lower level (on average) from those who are meeting the material for the first time.
The effect of the massive lack of conceptual understanding and learning is evident from a simple analysis of a typical Standard 8 examination in Mathematics. The median on the 2004 mathematics paper was 37%, and so half of the pupils earned less than 37% of the available marks. In order to get a respectable pass rate (67% of candidates passing), pupils were passed if they earned 22% of the marks or more.
Because of the four-way multiple choice questions for 60% of the paper, pupils would on average earn 15% by guessing. So, to reach 22% they only had to ‘earn’ 7%. For many pupils this is the final outcome of at least eight (often many more) years of struggle with mathematics in primary school. That so much effort is dedicated to passing this examination for so little success suggests a great waste of effort and time (Lowe, 2008).
Textbooks
Any textbooks are owned by school, as the children have no money to buy them. It is significant that only two of my six observed teachers actually made visible use of the textbook. Patricia brought out the only books she had (five of them) for her 120 pupils in Standard 2 (Lowe, 2008). The approved books are written by committee; as yet it is not permitted for schools to buy or to let children buy, books from publishers.
The textbooks are not written to remind teachers of exactly how the mathematics works or why. The standard introduction to an exercise contains one worked example, with no explanation. It seems to be an assumption by the textbook authors and writers of the teachers’ guides that teachers will not need to be reminded of the content they, supposedly, understood when doing their initial training. To this, add the fact that, from Standard 5 to 8, textbooks are in English – a second language for all pupils as well as teachers – and we can see why there is a lack of confidence in the ranks. (Lowe, 2008). As this policy was ‘about to be changed’ some years ago, I wrote mathematics texts for Standards 5 to 8 – the classes in English – but these have not yet been published, due to a reversal of this policy at the very last moment.
Group work is recommended in the teacher guides for the textbooks, but teachers have rarely experienced any group work, even in in-service courses run by the Ministry officials. Group activities in mathematics are not common, but I observed occasional group work in the classes observed in my research.
Initial teacher training
Due to the HIV-AIDS epidemic and the teacher shortage, the ‘training’ of most teachers has been conducted for one term (in a residential college) followed by another five terms alone in a classroom. Inservice courses are irregularly held, usually when some curriculum change is being introduced. These are normally lectures, although I witnessed some excellent group work taking place at one session.
References
Croft, A. (2002). Singing under a tree: does oral culture help lower primary teachers be learner-centred? International Journal of Educational Development, 22(3-4), 321–337. https://doi-org.ucd.idm.oclc.org/10.1016/S0738-0593(01)00063-3
Dienes, Z. P. (1971). Building up Mathematics (4th ed.). Hutchinson Educational.
Government of Malawi (2002). Malawi Poverty Reduction Strategy Paper. https://www.imf.org/external/np/prsp/2002/mwi/01/index.htm
IEQ/Malawi (2003). Exploring factors that influence teaching and learning: collection of selected studies using the IEQ/Malawi longitudinal data 1999-2002, Volume 2. American Institutes for Research, Malawi Institute of Education, Save the Children (USA).
Lowe, I. (2008). Policy and practice in rural primary education in Malawi: the case of mathematics teaching [PhD Thesis, Monash University]. Monash University Bridges. https://doi.org/10.4225/03/587837721ff96
Sandefur, J. (2016). Internationally comparable mathematics scores for fourteen African countries (Working Paper 444). Center for Global Development. https://www.cgdev.org/publication/math-scores-fourteen-african-countries
All photographs were taken by the author, except Figs. 7 & 9 which were taken by friends. Figs. 1, 2 and 9 appear with the permission of the subjects.
About the Author

Dr Ian Lowe worked in mathematics education from graduation to retirement at the age of 75. His varied career included innovative teaching in schools in Australia (Victoria) and Canada. He worked in curriculum departments and wrote many textbooks in Victoria, Canada, (Western) Samoa and Malawi, including two for the Australian Academy of Science. He researched education in (Western) Samoa (for his MEd) and Malawi leading to his PhD, awarded at the age of 68. For the last decade of his career he worked as a mathematics consultant for The Mathematical Association of Victoria, of which he is a Life Member.
Ian Lowe may be contacted through Kaye Stacey (k.stacey@unimelb.edu.au), the Editor-in-Chief for this issue of Educational Designer.